八大基本排序(详解)

前言
博主将在本文讲述选择,插入,希尔,快速,冒泡,堆排,归并排序,记数排序.

1.插入排序

1.1 直接插入排序

动图演示: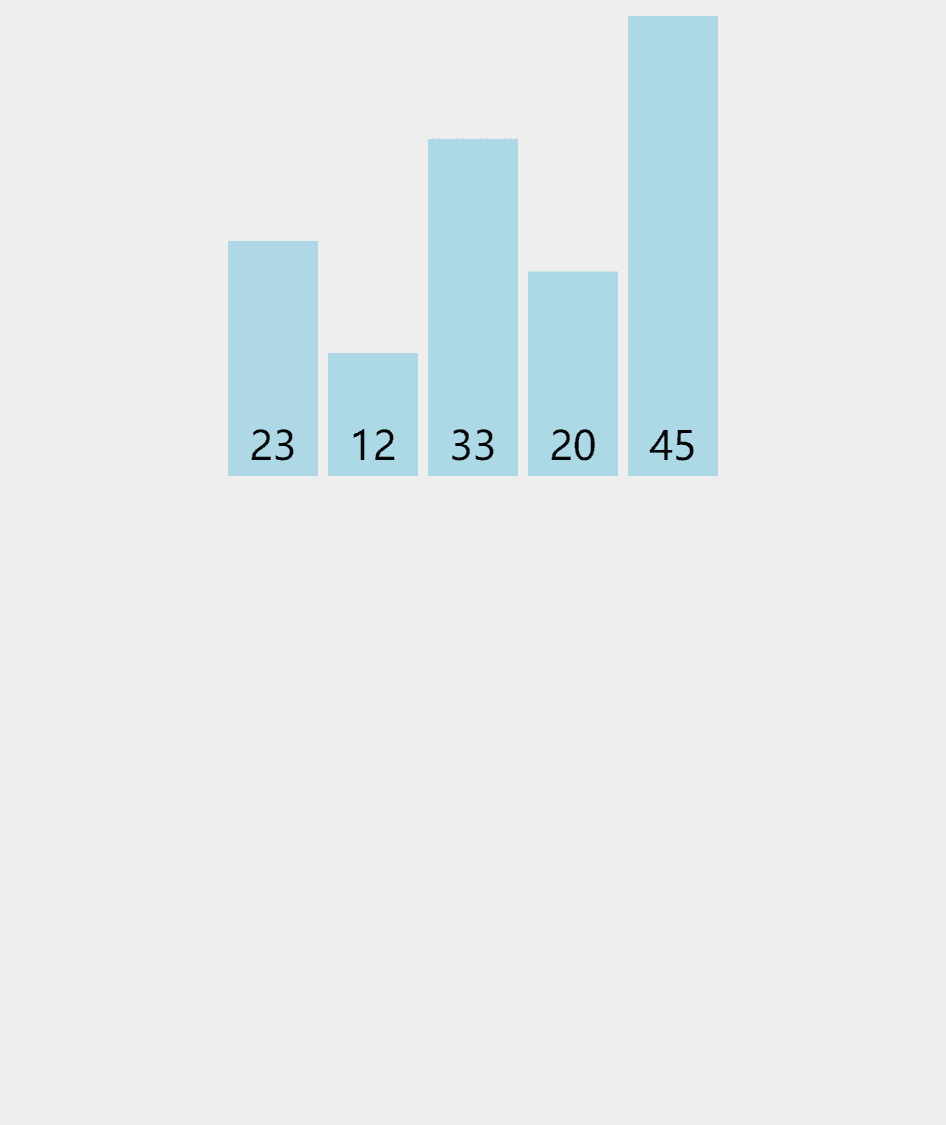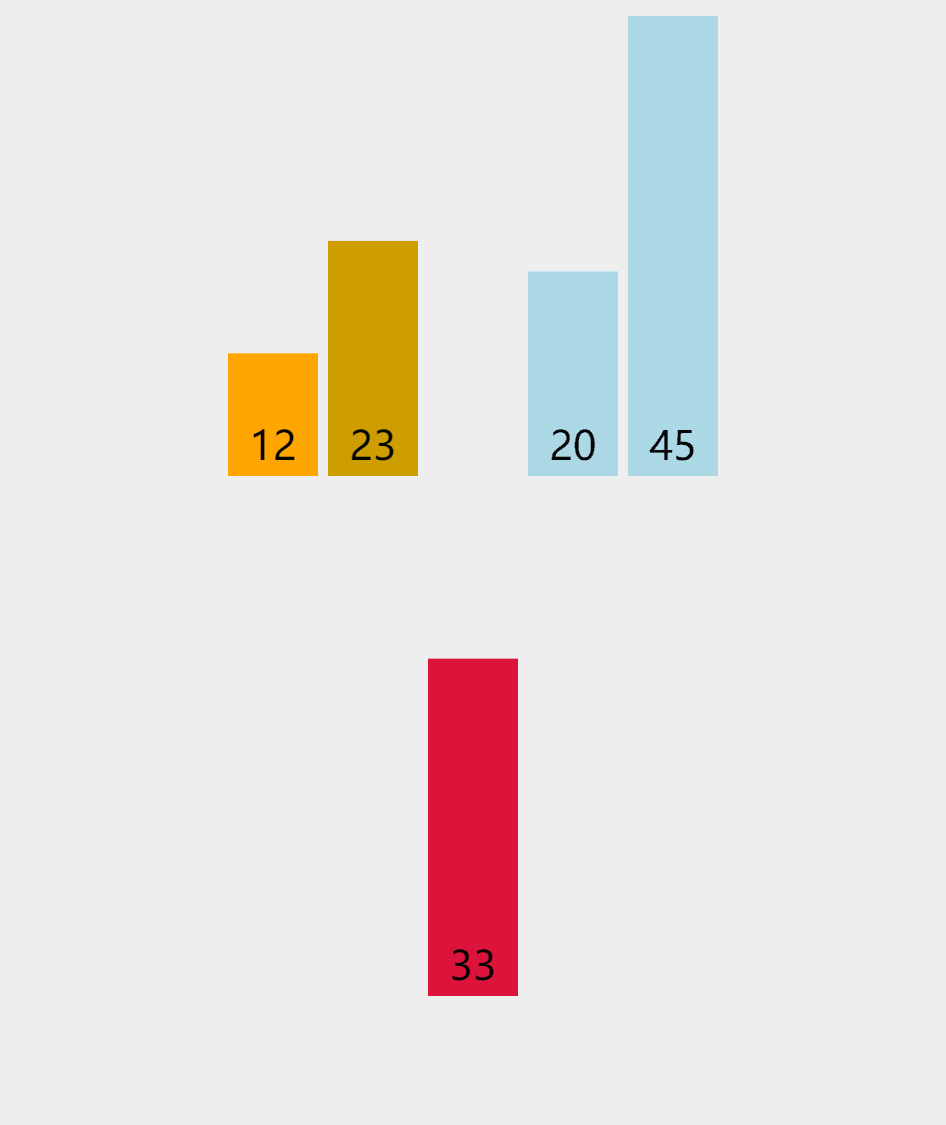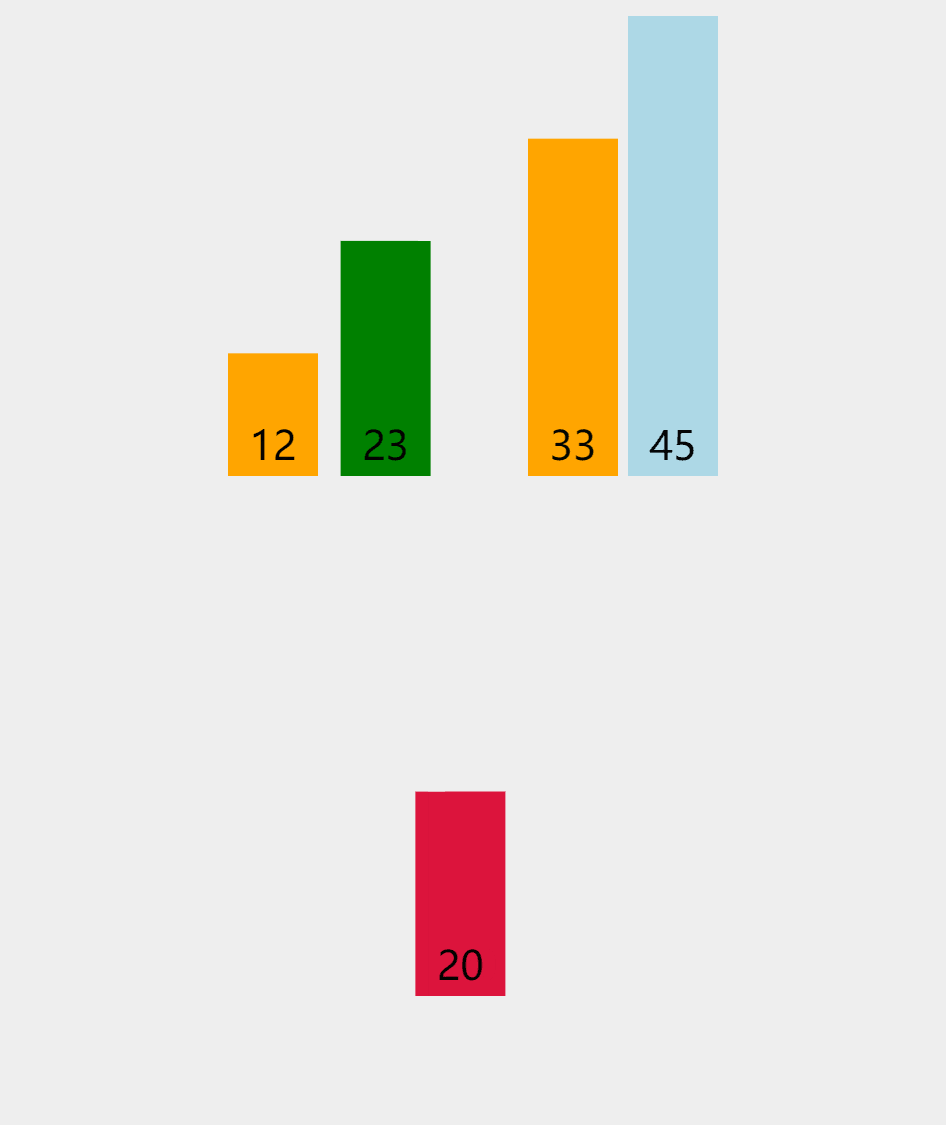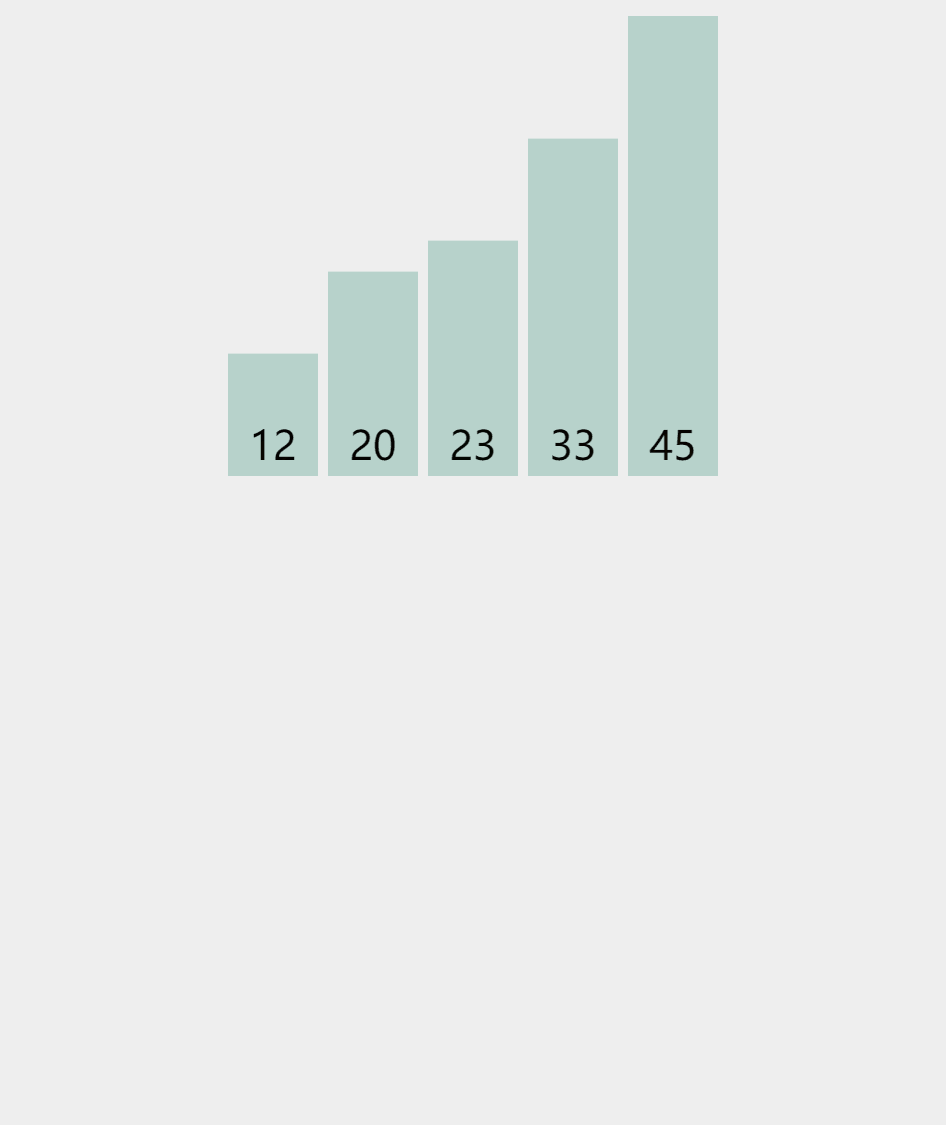

思路:

就像我们打牌时,一个一个插入一样

具体思想就是,我们在一个有序的数组中插入一个数,那么我们是将这个数在有序数组中依次比较,那么我们怎么将这个数据插入其中呢? 我们采用覆盖的方法,就是将后一个数等于前一个数这样依次覆盖,这样就会给我们要插入的数据留下一个空位,然后插入即可,可能大家会有疑问,一个无序的数组我们怎么插入呢??? 其实我们将第一个数看成一个数组,那么他不就是有序的吗,然后将第二个数插入,再插入第三个数. . . . . . .,这样就完成了排序

代码实现

void InsertSort(int* a, int n)
{
    
	for (int i = 0; i < n-1; i++)//可以分为n-1次插入,第一次就认为是有序,
	{
    
		int end = i;//记录每次插入的有序数组最后一个位置
		int tmp = a[end + 1];//记录插入的数据
		while (end >= 0)//一直比较到0下标位置
		{
    
			if (tmp< a[end])
			{
    
				a[end + 1] = a[end];//往后覆盖
				--end;
			}
			else
			{
    
				break;
			}
			a[end + 1] = tmp;//插入,不能放到else中,因为可能是else中break出来 也有可能是end>=0为假出来,也就是说tmp是在有序数组中是最小的数
		}	
		// 放这也行 a[end + 1] = tmp;//插入,不能放到else中,因为可能是else中break出来 也有可能是end>=0为假出来,也就是说tmp是在有序数组中是最小的数
	}
}

复杂度

空间复杂度:

O(1),未开辟额外空间

时间复杂度:

最好的情况:已经有序的情况下,只需遍历一次,即O(N)
最坏的情况:每插入一个数都要遍历,即F(N)=1+2+3+4+…+N=N(N-1)/2=O(N^2).

1.2希尔排序(缩小增量排序)

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

动图演示:

画图讲解:

从图中可知gap越大,分成的小数组越多,希尔排序就是通过这种小区间预排,让数组似有序化,从而减轻最后一次直接插入排序(gap=1)的遍历次数,从而提升速度!

代码

void ShellSort(int* a, int n)
{
    
	int gap = n;
	while (gap > 1)
	{
    
		gap = gap / 3 + 1;//避免gap=0,导致最后一次不为1,所以加上1,当为1的时候就是插入排序
		for (int i = 0; i < n - gap; i++)
		{
    
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)//拆分多组数组进行插入排序
			{
    
				if (tmp < a[end])
				{
    
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
    
					break;
				}
				a[end + gap] = tmp;
			}
		}
	}
}

希尔排序的特性总结：

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算.但是通过大量实验证明O(N^1.3)左右

2.选择排序

2.1.1单向选择排序

思路

就是再数组中找出最值,然后放入最左边,依次排放

动图演示:

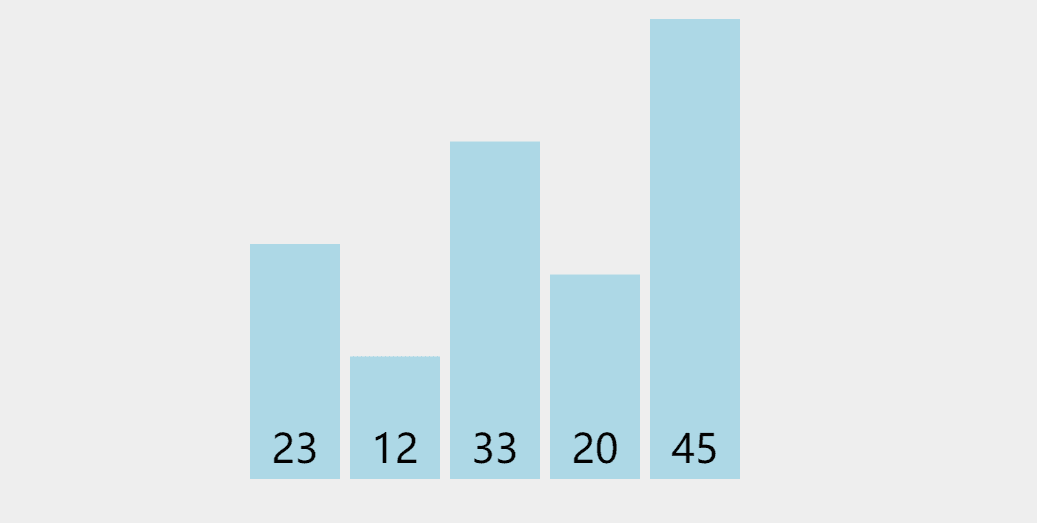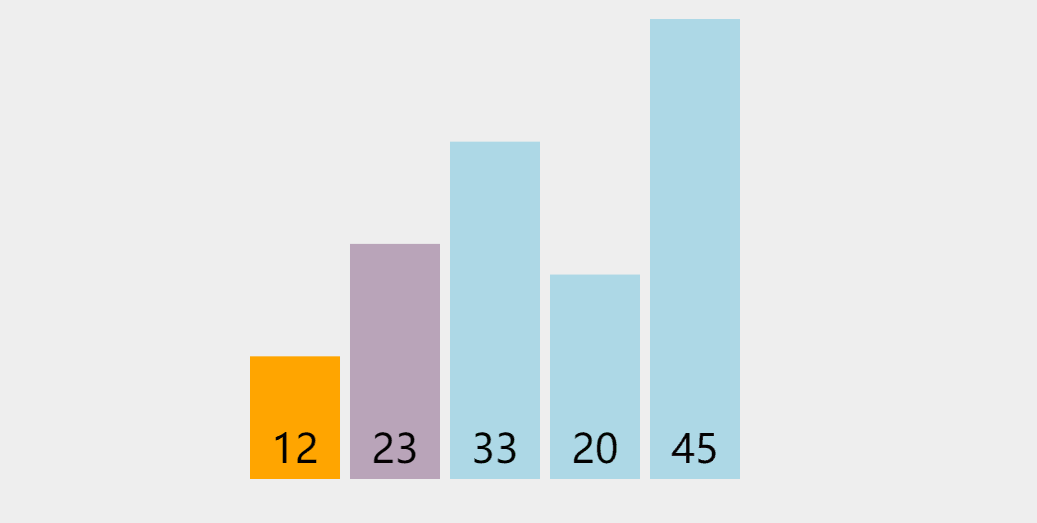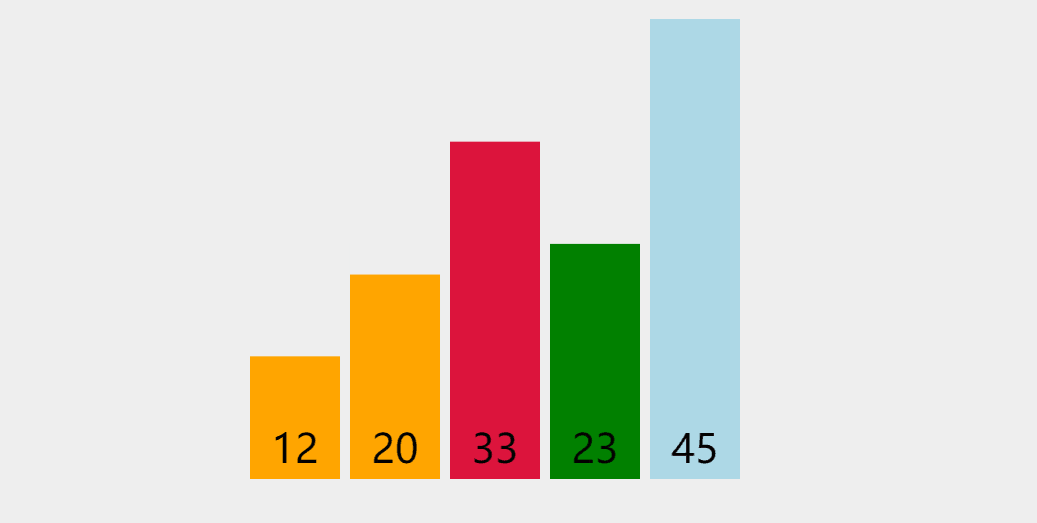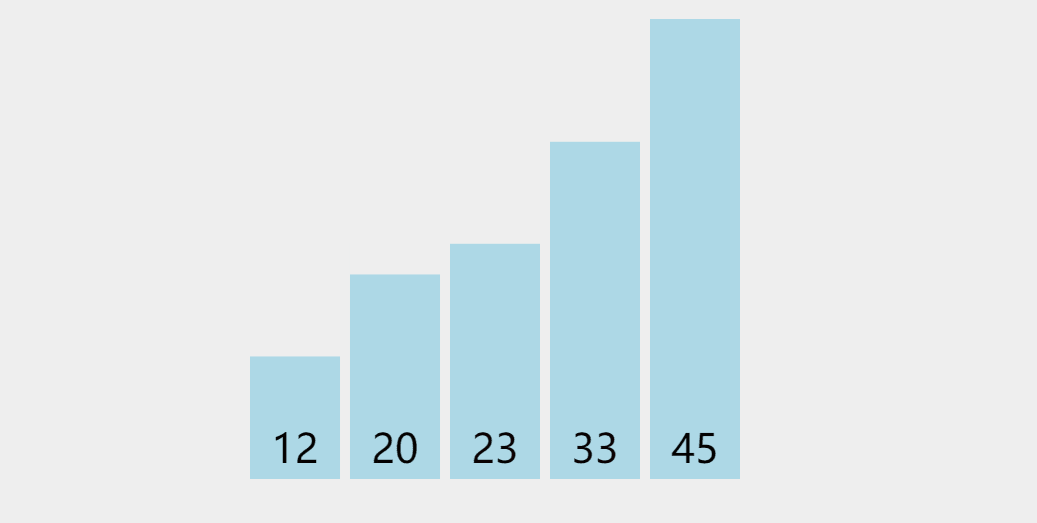
代码:

void SelectSort(int* a, int n)
{
    

	for (int i = 0; i < n; i++)
	{
    
		int index = i;
		for (int j = i + 1; j < n; j++)//找到最值的下标
		{
    
			if (a[index] < a[j])
			{
    
				index = j;
			}
		}
		Swap(&a[index], &a[i]);
	}
}

2.1.2 双向选择排序(对单向选择排序的优化)

代码

void SelectSort2(int* a, int n)
{
    
	int begin = 0;
	int end = n-1;
	while(begin<end)
	{
    

		int maxi = begin;
		int mini = begin;
		for (int j = begin; j <= end; j++)
		{
    
			if (a[maxi] < a[j])
			{
    
				maxi = j;
			}
			if (a[mini] > a[j])
			{
    
				mini = j;
			}
		}
		Swap(&a[maxi], &a[begin]);
		if (mini == begin)//因为上面的交换,maxi和begin交换了,当mini==begin时,说明begin是最小值,但是和maxi交换了,所以maxi现在是最小值
		{
    
			mini = maxi;	
		}
		int temp = 0;
		Swap(&a[mini], &a[end]);

		begin++;
		end--;
	}
}

复杂度

时间复杂度:O(N^2)
空间复杂度:O(1)

2.2 堆排序

看我这篇文章:二叉堆的实现(含堆排序讲解),点击直达

3.交换排序

3.1冒泡排序

思路:

相邻数据依次比较交换

代码:

void BubbleSort(int* a, int n)
{
    

	for (int j = 0; j < n - 1; ++j)
	{
    
		int exchange = 0;
		for (int i = 1; i < n - j; ++i)
		{
    
			if (a[i - 1] > a[i])
			{
    
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}

		if (exchange == 0)//exchange==0说明数据已经有序
		{
    
			break;
		}
	}
}

3.2 快速排序

思想;

任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
重点解决,单趟key的位置

代码模板:

void QuickSort(int* a, int begin, int end)
{
    

	while (begin >= end)
		return;
	int keyi = PartSort(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);

}

和二叉树的前序遍历很像!就是将数组分成最小单元,然后最小单元有序,那么上一层key值两边均有序,以此类推,完成排序!!

3.2.1 hoare版本

思路

先从key的反方向找小,假设key在左边,我们先让右边的right找到比key小的暂停,然后让左边的left找大,找到之后和right交换,然后right继续找,left然后也找,找到就交换,知道相遇之后,相遇位置的左边就是都比key小的,右边都是比key大的,我们让key的值和相遇点交换,然后key的位置到相遇点,这就完成了单趟交换,然后以key的左边,右边分别为一个数组,再完成交换!!

动图

代码:

int PartSort(int* a, int begin, int end)//hoare版本 这种就像是先走完再找key位置
{
    
	int left = begin;
	int keyi = left;
	int right = end;
	while (left < right)
	{
    

		while (left < right && a[right] >= a[keyi])//找小
			//这里为什么从keyi的反方向开始呢?? 因为在left和right相遇的时候,相遇的值的比a[keyi]小或者相等,即使right一路畅通无阻跑到keyi位置也没关系
			//这就是因为right就是找小的,最极端也就是相等,因为找小的先走的,所以相遇的时候一定是小的,如果从keyi的正方向走的话,相遇一定是大的啊,大的和a[keyi]交换肯定不对啊
			//我们就是需要找小的交换, 你找个大的算怎么回事呢?
		{
    
			right--;
		}
		while (left < right && a[left] <= a[keyi])//找大
		{
    
			left++;
		}
		Swap(&a[right], &a[left]);
	}
	Swap(&a[keyi], &a[left]);
	keyi = left;
	return keyi;
}

3.2.2 挖坑法

思路

将key的位置当做一个坑,然后right指针开始找小,找到小的就放入坑中(就是交换),然后left找大,找到就放入坑中,直到两个指针相遇停止,那么相遇的这个位置一定是坑,将key原始数据放入坑中,key的位置变成改坑的位置,和hoare版本很像,但是更容易理解!这就完成了单趟排序!

动图

代码

int PartSort(int* a, int begin, int end)//挖坑法,有效的帮助你理解 这种就像边走边找key位置
{
    
	int key = a[begin];
	int piti = begin;//坑位
	while (begin < end)
	{
    
		//从左找大,找到之后把它放坑位里,然后这里成为新的坑位
		while (begin < end && a[end] >= key)
		{
    
			end--;
		}
		a[piti] = a[end];//将大值放入坑位
		piti = end;//坑位到原来大值的位置
		//从左找小,找到之后把它放坑位里,然后这里成为新的坑位
		while (begin < end && a[begin] <= key)
		{
    
			begin++;
		}
		a[piti] = a[begin];//将小值放入坑位
		piti = begin;//坑位到原来小值的位置
	}
	a[piti] = key;
	return piti;//最后的坑位就是我们的key值
}

3.2.3 前后指针法

思路

前指针cur,后指针prev,前指针在前面依次找比key值小的,找到后就和prev交换位置,然后prev+1,重复执行,最后prev的位置就是key的分界点,所以让那个key和prev交换

动图

代码

int PartSort3(int* a, int begin, int end)//前后指针法 代码最简洁
{
    
	int cur = begin+1;
	int prev = begin;
	int keyi = begin;
	for (int i = begin; i < end; i++)
	{
    
		if (a[cur] <= a[keyi]&& prev++!=cur)//找大,找到最后prev往后腾一个位置和cur交换位置,就是cur去找大值,找到就往prev那边放,放完prev就跑一个
		{
    
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);//将keyi对应的数值和prev交换,让keyi变成分界线!
	keyi = prev;
	return keyi;
}

快速排序优化

优化1:

如果我们学过二叉树的话,我们应该key在数组中间的话,这个遍历的深度就越小,而且如果每次选到的key是这组数的最大值或者最小值的话，快排的效率就会变得非常低，几乎接近于O(N²),还可能因为递归深度太深导致栈溢出。,所以我们采取三数取中来进行优化!

代码

int GetMidIndex(int* a, int begin, int end)//三值取中
{
    
	int mid = (begin + end) / 2;
	if (a[begin] < a[mid])
	{
    
		if (a[mid] < a[end])
			return mid;
		else if (a[begin] < a[end])
			return end;
		else
			return begin;
	}
	else //(a[begin] >= a[mid])
	{
    
		if (a[mid] > a[end])
			return mid;
		else if (a[begin] < a[end])
			return begin;
		else
			return end;
	}
}

优化2

要知道，快排算法是不断递归来排一个数的左右两边，所以当快排算法越接近与结束的时候，左右两边数组越接近有序。
而快排算法对于接近有序的序列是没有任何效率上的提高的，但是我们知道插入排序时，如果一段序列越接近于有序，插入排序的效率就越高。
所以我们可以采用插入排序进行优化!!

代码

void QuickSort(int* a, int begin, int end)
{
    

	while (begin >= end)
		return;
	while (end - begin > 20)//优化,因为越小递归次数越多,就得不偿失了
	{
    
		int keyi = PartSort3(a, begin, end);
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
	InsertSort(a, end - begin+1);//数组下标差+1等于数组个数

}

快速排序非递归版

思路:

在设计单趟排序的时候,我们要知道改数组的头和尾,所以我们通过栈来实现非递归,将头和尾依次压入栈中,然后在单趟排序之前出栈,得到一个keyi值,这样我们又知道左右子区间的头和尾,继续进行压栈,这类似于二叉树的层序遍历

代码

void QuickSortNonR(int* a, int begin, int end)//快排非递归方法
{
    
	Stack q;
	StackInit(&q);
	StackPush(&q, end);
	StackPush(&q, begin);
	while (!StackEmpty(&q))
	{
    
		int left = StackTop(&q);
		StackPop(&q);
		int right = StackTop(&q);
		StackPop(&q);
		int keyi = PartSort3(a, left, right);
		//区间[keyi-1,left] keyi [keyi+1,right]
		if (keyi + 1 < right)
		{
    
			StackPush(&q, right);//因为先top的是left,所以left边最后放
			StackPush(&q, keyi+1);
		}
		if (keyi - 1 > left)
		{
    
			StackPush(&q, keyi-1);//因为先top的是left,所以left边最后放
			StackPush(&q, left);
		}
	}
	StackDestroy(&q);
}