m-way search trees

Binary tree and B Trees

The problem analysis of binary tree

The operation efficiency of binary tree is high , But there are also problems , Look at the binary tree below

1. Binary trees need to be loaded into memory , If the binary tree has fewer nodes , No problem , But if the binary tree has many nodes ( such as 1 Billion ), Just The following problems exist :
2. problem 1： When building a binary tree , It needs to be done many times i/o operation ( Massive data exists in databases or files ), Massive nodes , When building a binary tree , Speed has an effect .
3. problem 2： Massive nodes , It also causes the height of the binary tree to be very high , It will reduce the operation speed .

Multiforked tree

1. In a binary tree , Each node has data items , Up to two child nodes . If each node is allowed to have more data items and more children , It's a multi branched tree （multiway tree）
2. We'll talk about it later 2-3 Trees ,2-3-4 A tree is a multi branched tree , By reorganizing nodes , Reduce the height of the tree , Can optimize the binary tree .
3. Illustrate with examples ( below 2-3 A tree is a multi branched tree )
   

B A basic introduction to trees

B By reorganizing the nodes , Lower the height of the tree , And reduce i/o Read and write times to improve efficiency .

1. Pictured B By reorganizing the nodes , Lowered the height of the tree .
2. The designers of file system and database system make use of the principle of disk read ahead , Set the size of a node equal to a page ( Page size is usually 4k), In this way, each node only needs one time I/O You can load it completely .
3. The degree of the tree M Set to 1024, stay 600 Of the billion elements, you only need 4 Time I/O Operation can read the desired element , B Trees (B+) widely Applied to file storage system and database system

2-3 Trees

2-3 Trees are the simplest B Tree structure , It has the following characteristics :

1. 2-3 All the leaf nodes of the tree are on the same layer .( As long as it is B Trees all satisfy this condition )
2. A node with two child nodes is called a two node node , Two nodes or no child nodes , Either there are two child nodes .
3. A node with three child nodes is called a three node , Three nodes or no child nodes , Or there are three child nodes .
4. 2-3 A tree is a tree composed of two nodes and three nodes .

2-3 Tree application case

Will be in series {16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} To build a 2-3 Trees , And ensure the order of data insertion .( Show me how to build 2-3 Tree process .)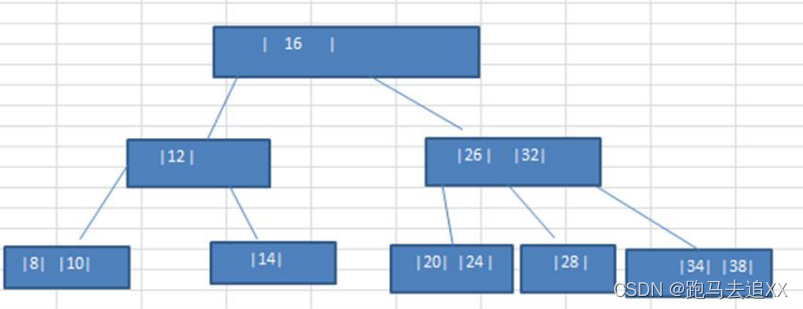

Insert rules :

1. 2-3 All the leaf nodes of the tree are on the same layer .( As long as it is B Trees all satisfy this condition )
2. A node with two child nodes is called a two node node , Two nodes or no child nodes , Either there are two child nodes .
3. A node with three child nodes is called a three node , Three nodes or no child nodes , Or there are three child nodes
4. When a number is inserted into a node according to the rules , Can't meet the above three requirements , You need to dismantle , Take it up first , If the upper floor is full of , Remove this layer , It still needs to meet the above requirements after dismantling 3 Conditions .
5. For a three node subtree, the value size still follows (BST Binary sort tree ) The rules of

Other instructions

except 23 Trees , also 234 Trees, etc , Concepts and 23 Trees are like , It is also a kind of B Trees . Pictured :

B Trees 、B+ Trees and B* Trees

B Introduction to the tree

B-tree A tree is a tree B Trees ,B namely Balanced, Balance means . Someone put B-tree Translate into B- Trees , It's easy to misunderstand . Would think B- A tree is a kind of tree , and B A tree is another kind of tree . actually ,B-tree It means B Trees .
I've already introduced 2-3 Trees and 2-3-4 Trees , They are B Trees ( English ：B-tree It's also written as B- Trees ), Here's another explanation , We are learning xi Mysql when , It is often said that a certain type of index is based on B Trees or B+ Treelike , Pictured :

For the illustration above :

1. B The steps of the tree ： The maximum number of child nodes of a node . such as 2-3 The steps of the tree are 3,2-3-4 The steps of the tree are 4
2. B- Tree search , Start at root , For keywords in nodes （ Orderly ） Sequence binary search , If it hits, it ends , Otherwise, enter the query The child node of the range to which the keyword belongs ; repeat , Until the corresponding son pointer is null , Or it's already a leaf node
3. The keyword set is distributed throughout the tree , That is, leaf nodes and non leaf nodes both store data .
4. The search may end at a non leaf node
5. Its search performance is equivalent to a binary search in the keyword set

B+ Introduction to the tree

B+ Trees are B A variation of a tree , It's also a multi-path search tree .

For the illustration above :

1. B+ Tree search and B Trees are basically the same , The difference is that B+ A tree hits only when it reaches the leaf node （B Trees can hit at non leaf nodes ）, Its nature Can also be equivalent to doing a binary search in the complete set of keywords
2. All keywords appear in the linked list of leaf nodes （ That is, data can only be stored in leaf nodes 【 Also called dense index 】）, And the keywords in the linked list ( data ) It happens to be orderly .
3. It's impossible to hit at a non leaf node
4. The non leaf node is equivalent to the index of the leaf node （ Sparse index ）, Leaf node is equivalent to storage （ keyword ） Data layer of data
5. More suitable for file index system
6. B Trees and B+ Each tree has its own application scenarios , Can't say B+ Trees are more than B Good tree , vice versa .

B* Introduction to the tree

B Trees are B+ A variation of a tree , stay B+ The non root and non leaf nodes of the tree increase the pointer to the brother .

B Description of the tree :

1. B* The tree defines that the number of keywords of non leaf nodes is at least (2/3)*M, That is, the minimum utilization rate of the block is 2/3, and B+ The minimum usage of tree blocks is 1/2.
2. From 1 We can see that ,B* The probability ratio of a tree to allocate new nodes B+ Trees should be low , More space use