Understanding of P value

One . Yes Understanding of value

1. Yes Intuitive understanding of values

What is? Is it worth it ？ Value is when the original assumption is true , The probability of more extreme results than the sample observations obtained . This statement may be more abstract , A more direct explanation is as follows ： stay Under the distribution curve , From sampling It's worth drawing a line （ Bilateral inspection is two lines ）, The shadow area from this line to the extreme direction is value . If , Then accept . If , Then refuse .

2. Through single sample bilateral Verify understanding value

Suppose Mr. Wang's class 20 Students' English scores are ：136, 136, 134, 136, 131, 133, 142, 146, 137, 140, 134, 135, 136, 132, 119, 132, 145, 131, 140, 141. Average score of the whole school . Is there any significant difference between Mr. Wang's average class score and the overall average score of the whole school ？ hypothesis （ That is, the sample of Mr. Wang's class comes from the average score A total of points ）. Use R The language code implementation is as follows ： among ,wang_class In Mr. Wang's class 20 Students' English scores ,mu=137 Represents the overall mean ,alternative="two.sided" Indicates single sample bilateral test . The output is as follows ：
(1)t=-0.90834,df=19,p-value=0.3751： respectively t value 、 Degrees of freedom and p value .
(2)alternative hypothesis： Indicates alternative assumptions , namely .
(3)95 percent confidence interval：95% confidence interval .
(4)mean of x： Sample mean .
hypothesis , because , Then accept , That is, there is no significant difference between Mr. Wang's average class score and the overall average score of the whole school .
explain ： Single sample The essence of the test is whether a single sample comes from a known population .

3. Through double sample bilateral Verify understanding value

Double sample Inspection and independent samples Testing is one thing . hypothesis grou1 and group2 The two sets of data satisfy normality （ Use shapiro.test Calculation ）、 Independence and homogeneity of variance （ Use var.test Calculation ）. Use t.test() Conduct test ： because , So we can't reject the original hypothesis , That is, there is no significant difference between the two groups of samples .
explain ： Double sample The essence of the test is whether two samples come from the same population .

Two . Review of probability and statistical knowledge

1. Probability knowledge

1.1 Key probability definitions

   Common concepts in probability theory are multiplication formulas , All probability formula , Bayes' formula , sample space , A random variable ,（ union | edge | Conditions ） Distribution function ,（ union | edge | Conditions ） Distribution law ,（ union | edge | Conditions ） Probability density , Bernoulli's test , The heavy Bernoulli experiment , The digital characteristics of random variables （ Mathematical expectation | variance | Standard deviation | covariance and correlation coefficient | Moment | Covariance matrix ）, Chebyshev inequality, etc . Here we will focus on random variables 、 Distribution function 、 Probability density this 3 A concept :

(1) A random variable

   Strictly define ： Let the sample space of the random trial be , Is defined in the sample space Upper Real valued single valued function , call Is a random variable .

• A random variable ： A real valued single valued function defined in the sample space . That is, the random variable is a function , Its domain is the sample space , The range of values is a real value , The essence of random variables is to map the sample space to real values .
• sample space ： take Randomized trials The set of all possible results in is called the sample space .
• Randomized trials ： Can be repeated under the same conditions ; There is more than one possible result per trial , And all possible results of the test can be determined in advance ; It is impossible to determine which result will appear before conducting a test .

(2) Distribution function

Strictly define ： set up It's a random variable , Is any real number , function

be called Distribution function of . This definition looks very abstract , Is there any specific physical meaning ？ For any real number , that ：

So if you know Distribution function of , You can calculate any interval On the probability of . Distribution function is a tool for studying random variables , The statistical regularity of random variables is described .

(3) Probability density

If you have a random variable Distribution function of , There are nonnegative functions , For any real number Yes

So the function Namely Probability density of （ Or probability density function ）, also It's a continuous random variable . What is the intuitive physical meaning of probability density ？ Through the equation You know ： Fall in the range On the probability of Is the curve on this interval The area under .

1.2 Distribution law of discrete random variables

• 0-1 Distribution
• The binomial distribution
• Poisson distribution

1.3 Probability density of continuous random variable

• Uniform distribution
• An index distribution
• Normal distribution （ Gaussian distribution ）

1.4 Law of large Numbers

The law of large numbers describes that the arithmetic mean of the first terms of a random variable sequence converges to the arithmetic mean of the mean of these terms under certain conditions .

(1) Weak large number theorem ( Schinchin's law of large Numbers )

set up It's independent of each other , A sequence of random variables that obey the same distribution , Have a mathematical expectation . front The arithmetic mean of variables , For any ：

Weak large number theorem ( Schinchin's law of large Numbers ) What physical meaning does it express ？ The essence is that for independent identically distributed and mean value Random variable of , When Their arithmetic mean when large Probably close to .

(2) Bernoulli's theorem of large numbers

set up yes {n} Events in the first independent repeat test Number of occurrences , Is the event The probability of occurrence in each test , So for any positive number ：

What physical meaning does Bernoulli's theorem of large numbers express ？ In essence, when the number of tests is very large , The probability of an event can be replaced by the frequency of the event .

1.5 Central limit theorem

The central limit theorem is to determine under what conditions , The distribution of the sum of a large number of random variables is close to the normal distribution .

(1) The central limit theorem of independent identical distribution

Set the random variable Are independent of each other , Obey the same distribution , And the mathematical expectation and variance are ：, Sum of random variables Standardized variable of ：

Distribution function of For any Satisfy ：

What physical meaning does the central limit theorem of independent identically distributed express ？ That is, when the mean value is , The variance of Independent identically distributed random variables of The sum of the Standardized variable of , When Sufficiently large ：

(2) Lyapunov theorem （ A little ）

(3) Di morph - Laplace's theorem

Set the random variable The compliance parameter is The binomial distribution of , For any Yes ：

Di morph - What physical meaning does Laplace theorem express ？ In essence, the positive distribution is the limit distribution of binomial distribution , When Sufficiently large , The above equation can be used to calculate the probability of binomial distribution .

2. Statistical knowledge

2.1 Statistics and sampling distribution

Sampling distribution is the distribution of statistics , So what is a statistic ？ set up It's from the population A sample of , yes Function of , If There are no unknown parameters in the , that Is a statistic .

(1) Common statistics

Sample average ：
Sample variance ：
Sample standard deviation ：
sample rank ( origin ) Moment ：
sample Moment of order center ：

(2)3 Large sample distribution ： Distribution

set up It's from the population The sample of , It's called a statistic Obey the degree of freedom as Of Distribution , Write it down as .
The distribution probability density function is as follows 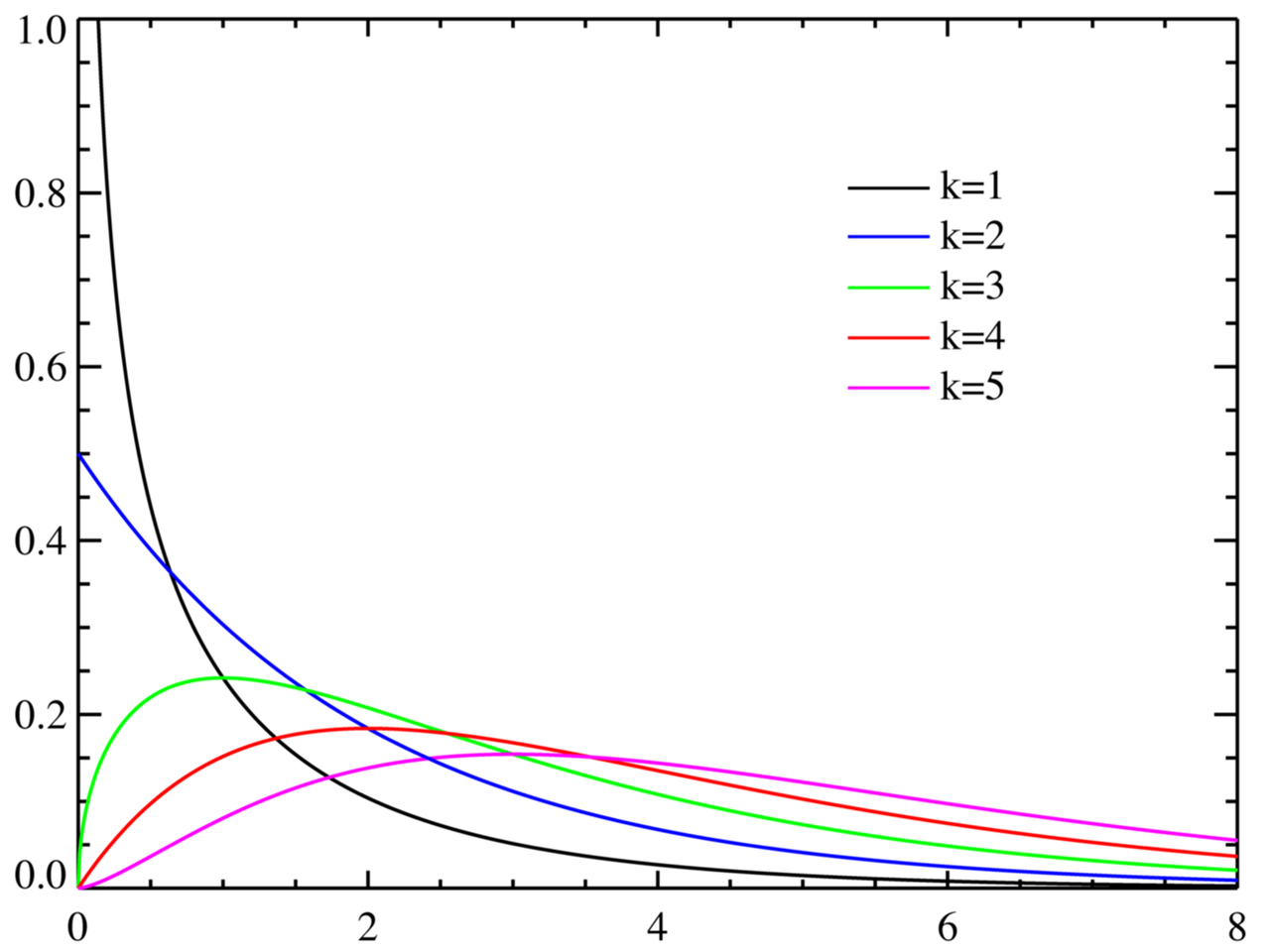： The cumulative distribution function of the distribution is as follows ：

(3)3 Large sample distribution ： Distribution

set up , also Are independent of each other , Call random variables Obey the degree of freedom as Of Distribution , Write it down as .
The distribution probability density function is as follows ： The cumulative distribution function of the distribution is as follows ：

(4)3 Large sample distribution ： Distribution

set up , And Are independent of each other , Call random variables Obey the degree of freedom as by The distribution of , Write it down as .
The distribution probability density function is as follows ： The cumulative distribution function of the distribution is as follows ：

2.2 Parameter estimation

   Parameter estimation and hypothesis testing are two basic problems in statistical inference , Parameter estimation includes point estimation and interval estimation . So what is a point estimate ？ Set the overall The form of the distribution function of is known , But one or more of its parameters is unknown , Use overall The problem of estimating the value of a population unknown parameter by a sample of is called the point estimation problem of parameters .
   To be specific, it is to set the overall Distribution function of The form of is known , It's the parameter to be estimated . yes A sample of , Is a corresponding sample value . The point estimation problem is to construct an appropriate statistic , With its observations As an unknown parameter Approximate value , call by An estimate of , call by The estimate of .
   Moment estimation and maximum likelihood estimation are two common methods to construct estimators . There must also be a good or bad evaluation criterion for the choice of estimators , That is unbiased 、 Effectiveness and consistency .

(1) unbiasedness ( Mean angle )

If the estimator Mathematical expectation There is , And for any Yes , So called yes An unbiased estimator of .

(2) effectiveness ( Variance angle )

set up And All are An unbiased estimator of , If for any , Yes And at least for one The inequality sign in the above formula holds , that a It works .

(3) Consistency

set up Is the parameter An estimate of , If for any , When when Converges in probability to , said by The consistent estimator of . namely .
explain ： A simple understanding of the confidence interval is that this interval contains parameters The credibility of truth value .

2.3 Hypothesis testing

   A simple understanding of hypothesis testing is to put forward a certain hypothesis , Then the process of determining whether the hypothesis is true , Either receive , Or refuse . But there are many concepts involved , For example, the level of significance 、 Original hypothesis and alternative hypothesis 、 Test statistic 、P value 、 There are two errors in hypothesis testing 、 Single and double test 、 Hypothesis test method （ test | test | Chi square test ）. In practice, single samples are often used Inspection and double samples test . The general process of hypothesis testing is as follows ：

• Put forward the original hypothesis and alternative hypothesis ： Take the proposition that cannot be easily denied without sufficient reasons as the original hypothesis , Take the proposition that is not sure enough and cannot be easily confirmed as an alternative hypothesis
• Choose the appropriate statistics , Determine its distribution form
• Specify the level of significance , Determine its critical value ： The significance level indicates the probability of rejecting the original hypothesis when the original hypothesis is true , That is, the risk of rejecting the original assumption . Through the value of 0.1、0.05、0.01
• Calculate the value of the check statistic
• Draw a conclusion

2.4 Multivariate statistics

   Multivariate statistics is a statistical discipline that studies the correlation and dependence between multiple random variables and the inherent statistical regularity . Including regression analysis , variance analysis , Factor analysis , Canonical correlation analysis , Clustering analysis , discriminant analysis , Principal component analysis , Mixed effect model, etc .

reference ：
[1] Probability theory and mathematical statistics （ Zhejiang University 4 edition ）
[2] Understand the hypothesis test ：https://blog.csdn.net/weixin_42327743/article/details/112568365
[3] Introduction to the principles of popular statistics ：https://www.bilibili.com/video/BV1x64y1B71k

Artificial intelligence dry goods recommendation Focus on technology sharing in the field of artificial intelligence

Game metauniverse Focus on technology sharing in the game field