当前位置:网站首页>【C语言】剖析函数递归(3)
【C语言】剖析函数递归(3)
2022-08-02 13:04:00 【凡人编程传】
作者:凡人编程传
系列:C语言初阶(适合小白入门)
说明:以凡人之笔墨,书写未来之大梦

₪前言
这一节,咱们把递归的最后两道题讲了,递归这个知识点的内容就全部完成了,好了,废话不多说,咱们直接进入正题了!
₪求一个数的阶乘(递归实现)
这道题熟悉吧,在循环结构的文章里面的练习题讲过的。不过这次咱们要用递归来实现。那么怎么实现呢?
这里再介绍一下递归的执行过程:递归氛围分为两个执行过:回推和递推。
1.回推:回推就是根据要解决复杂的问题去找到类似于大复杂问题,简单问题最基本的解。这个过程需要系统内存的栈存储临时变量的值;
2.递推:递推就是根据找到简单问题的解去得到复杂问题的解,这个过程是逐步释放之前栈空间所保存的变量,直到得到复杂问题的解。
那么这个问题的回推过程是什么呢?看例子吧:
根据数学知识,一个数的阶乘是上一个数的阶乘与这个数字本身相乘。如3!(这里的感叹号是数学里面的阶乘符号,不是逻辑非)为3!=3*2!
那么我们要求n的阶乘也就是如下:
n!=n * (n-1)
(n-1)!=(n-1) * (n-2)!
(n-2)!=(n-2) * (n-3)!
…
2!=2 * 1!
1!=1* 0!;
0! = 1 (0是最小的阶乘数,规定值为1)
从上述例子可以看出,如果想要知道n的阶乘,那么就必须要先知道(n-1)! * n,想要知道(n-1)!就必须先要知道,(n-2)! * n(n-1)。这个过程也就是函数自己调用自己的过程,以此类推,直到我们回推到知道的最基本知识点0!=1,就可以开始递推了。
递推:
回推到我们知道的0!=1;
0!=1;
1!=1 * 1 (1!=1 * 0!)
2!=2 * 1. (2!=2 * 1!)
3!=3 * 2 (3!=3 * 2!)
…
n!=n*(n-1)!
根据0!=1这个已知的基本条件,得到1!,2!,3!..最终得到n!
另外再说一点,n是可能是负数的,因为最小的阶乘是0!。所以写代码时注意罗列分支。
有了以上知识,我们就知道代码怎么写了。
code:
#include<stdio.h>
int fac(int k)
{
if(k<0)
{
return -1; //没有负数的阶乘
}
if(0==k)
{
return 1; //0的阶乘为1
}
else
{
return k*fac(k-1);
}
}
int main()
{
int n;
scanf("%d",&n);
int t=fac(n);
if(t<0)
{
printf("参数错误!没有负数的阶乘!\n");
}
else
{
printf("%d!=%d",n,fac(n));
}
return 0;
}
测试结果: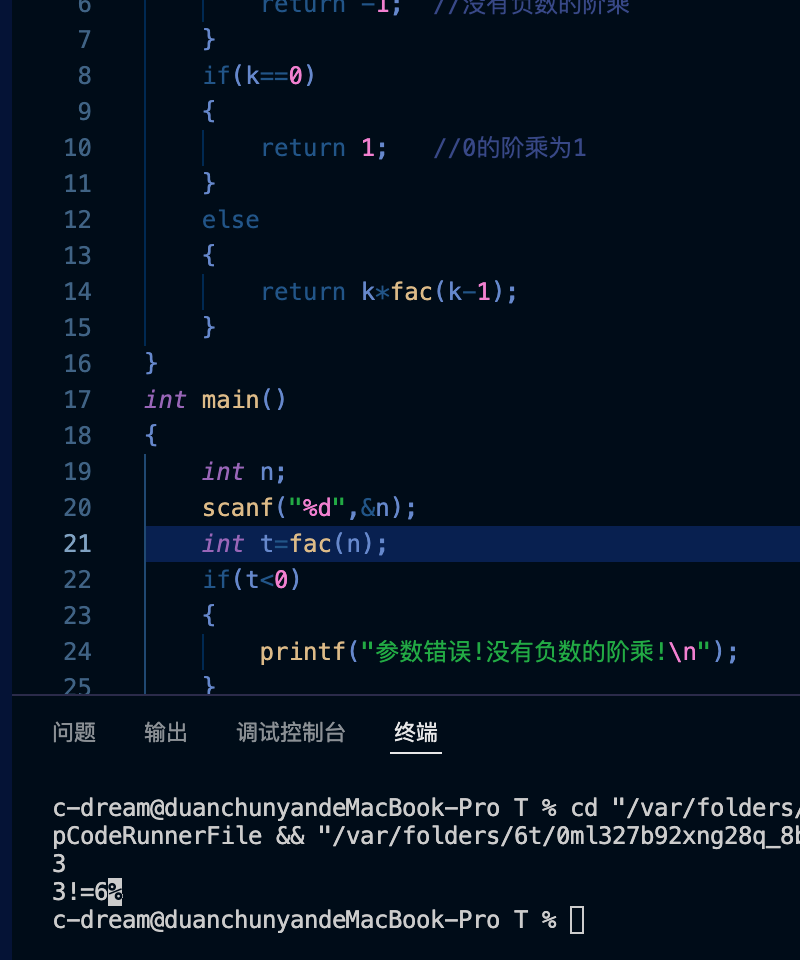
₪求斐波那契数列的第n项
这道题和上一道题很类似,根据数学知识可以知道基本条件,斐波那契数列的前两项都为1,且从第3项开始,每项是前两项的和。
如: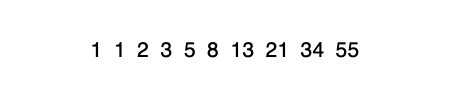
2=1+1
3=2+1
5=2+3
…
n=(n-2)+(n-1)
可以看出,每一项都是前两项之和。那么我们就可以根据这个规律和一个已知的基本条件前两项是1,来进行回推和递推了。
回推:
n=(n-1)+(n-2)
(n-1)=(n-3)+(n-2)
(n-2)=(n-4)+(n-3)
…
这里我们画一个图来更容易理解;
这里假设n为50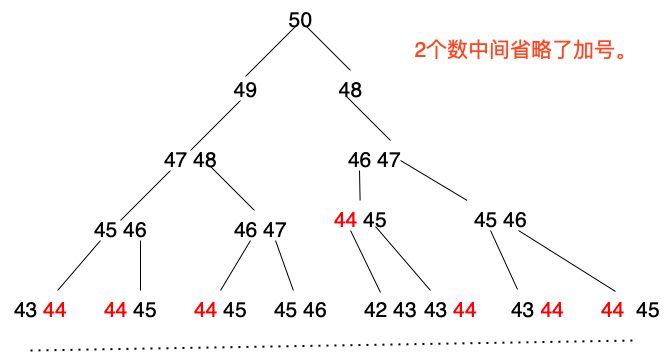
我们可看到,1个数去回推另两个数来求和,还有就是44这个数被重复计算了很多次。这还只是第4次回推,要一直推到1,也就是2的49次方,那这些数据要被重复计算多少次?这是否会导致我们的效率低。
递推:
递推就是一直回推到那个已知条件前两项为1,就可以开始求第3项的(1+1=2),第4项(2+1=3)以此类推到n。也就是上图的倒过来开始求项。
有了以上知识,就可以写出代码了
code:
#include<stdio.h>
int Fib(int k)
{
if(k>2) //不是前两项,从第3项开始
{
return Fib(k-1)+Fib(k-2);
}
else if(k>=1)
{
return 1; //前两项是1
}
}
int main()
{
int n;
scanf("%d",&n);
printf("第%d项=%d",n,Fib(n));
return 0;
}
测试结果: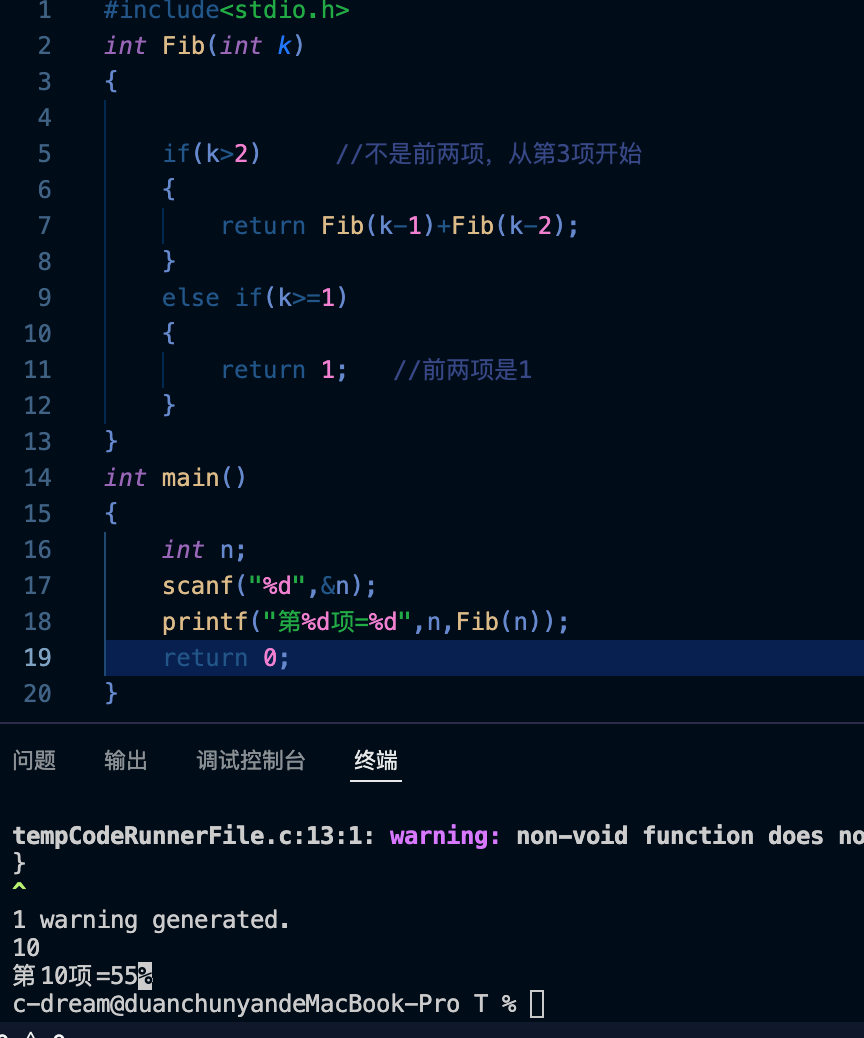
但是递归用到这种需要大量重复计算的题上效率太低了。如果要求的项大了计算机是需要很久才算得出来的,我们来测试求第40项一下第3项2被重复计算了多少次
code
#include<stdio.h>
int count=0; //定义全局变量来增大生命周期,保证count在整个项目中有效
int Fib(int k)
{
if(k==3)
{
count++;
}
if(k>2) //不是前两项,从第3项开始
{
return Fib(k-1)+Fib(k-2);
}
else if(k>=1)
{
return 1; //前两项是1
}
}
int main()
{
int n;
scanf("%d",&n);
printf("第%d项=%d\n",n,Fib(n));
printf("count=%d",count);
return 0;
}
测试结果: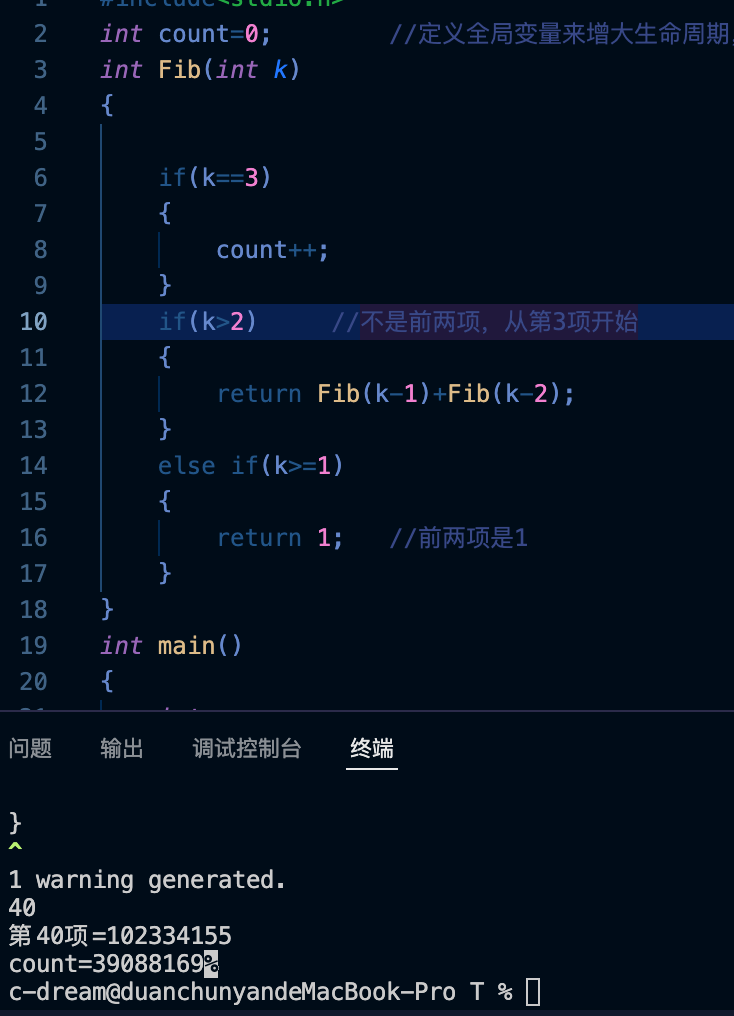
三千多万次!可见这个时间复杂度有多差,效率高低一看便知。
那么咱们这道题能不能换个写法?能!斐波那契数列反正是的第n项反正是前两项的和嘛。咱们从前往后加不就完了,这样就可以避免多次重复计算一个数字,不用像递归一样去找前n个数回来计算又重新算那个数。
循环来写的主要关键就是从前往后面算的时候,先把第n个数用(n-1)+(n-2)算出来,然后要求第n+1个数的时候把n-1改为n-2,n-2又改为n.可能有点看不懂,没关系咱们看图。
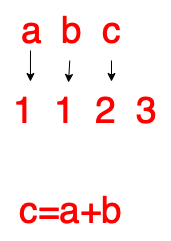
这是求第3项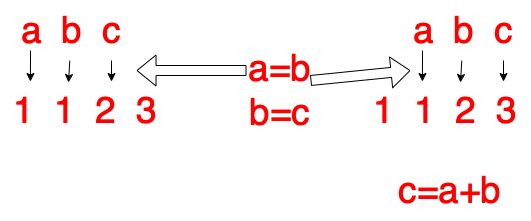
求第4项
还有注意,每次循环就算出来一个数,那么就离n更近了一步最后求n只需算到n-1即可与n-2相加得到n,有了以上知识就可以敲代码了:
code:
#include<stdio.h>
long long Fib(int k) //这里测试第50项,防止整形溢出所以设为long long 类型
{
long long a=1,b=1,c=1; //已经知道前两项,c设1应付当n<-2时也就是求前两项为1,所以设为1
while(k>2)
{
c=a+b;
a=b;
b=c;
k--;
}
return c;
}
int main()
{
int n;
scanf("%d",&n);
printf("第%d项=%lld\n",n,Fib(n));
return 0;
}
运行结果:
这时候得出结果就很快了,因为计算机不需要大量重复计算了。
₪结言
好了,函数递归这一章节的内容到此结束,希望你有收获,期待下一章节的数组吧!
边栏推荐
- 节省50%成本!京东云重磅发布新一代混合CDN产品
- To eliminate air bubbles to save the mushroom h5 small game source code
- 设置代理服务器(谷歌+IE)「建议收藏」
- Automatically generate code generator recommendation-code-gen
- sql concat() function
- Custom mvc framework review
- FreeRTOS creation tasks - dynamic creation, static creation
- 无线振弦采集仪远程修改参数方式
- Name conventions in FreeRTOS
- Taurus.MVC V3.0.3 microservice open source framework released: Make the evolution of .NET architecture easier in large concurrency.
猜你喜欢
How to use the database like tap water?|Tencent Cloud Database TDSQL-C
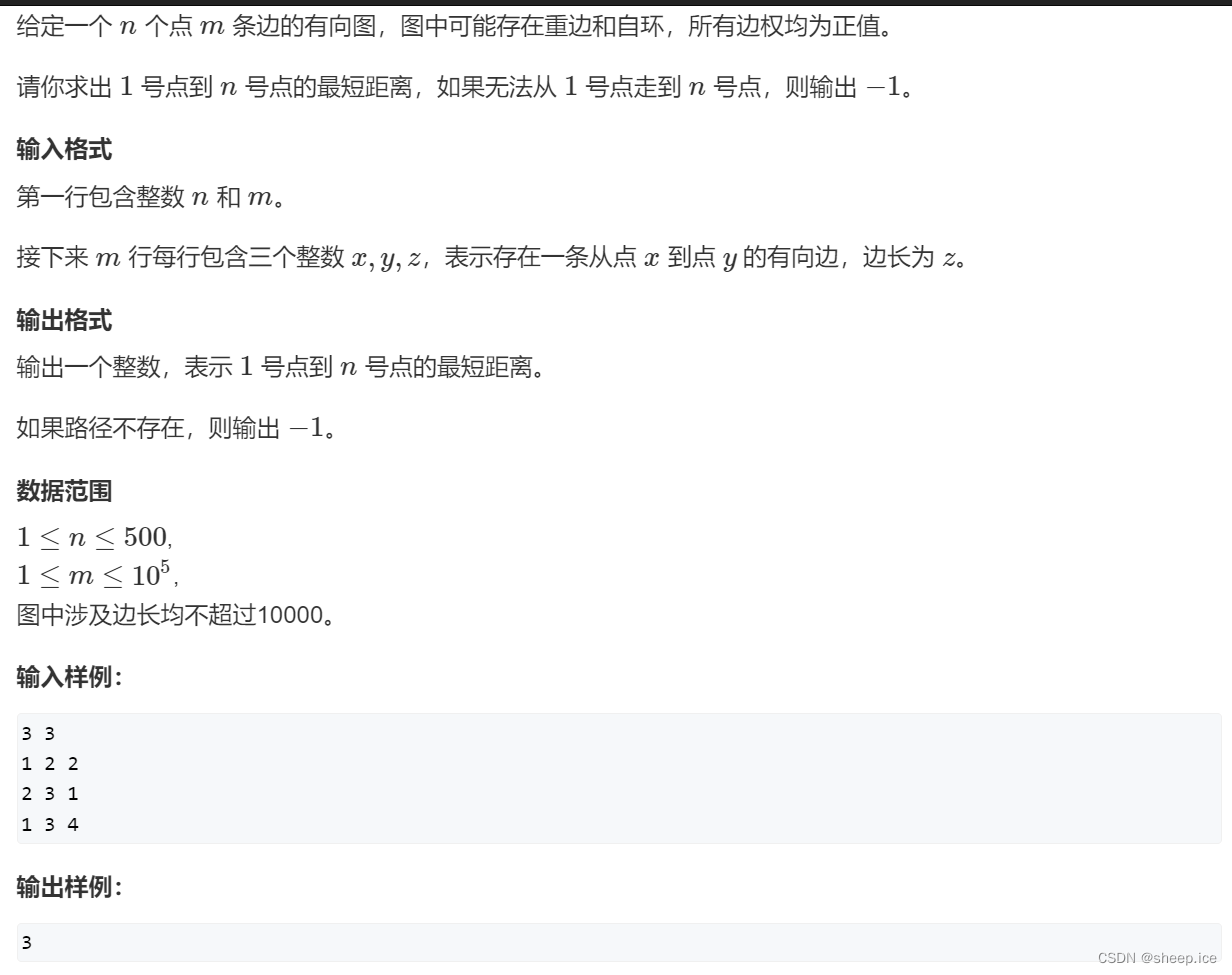
你知道图论的Dijkstra吗?
Redis全部
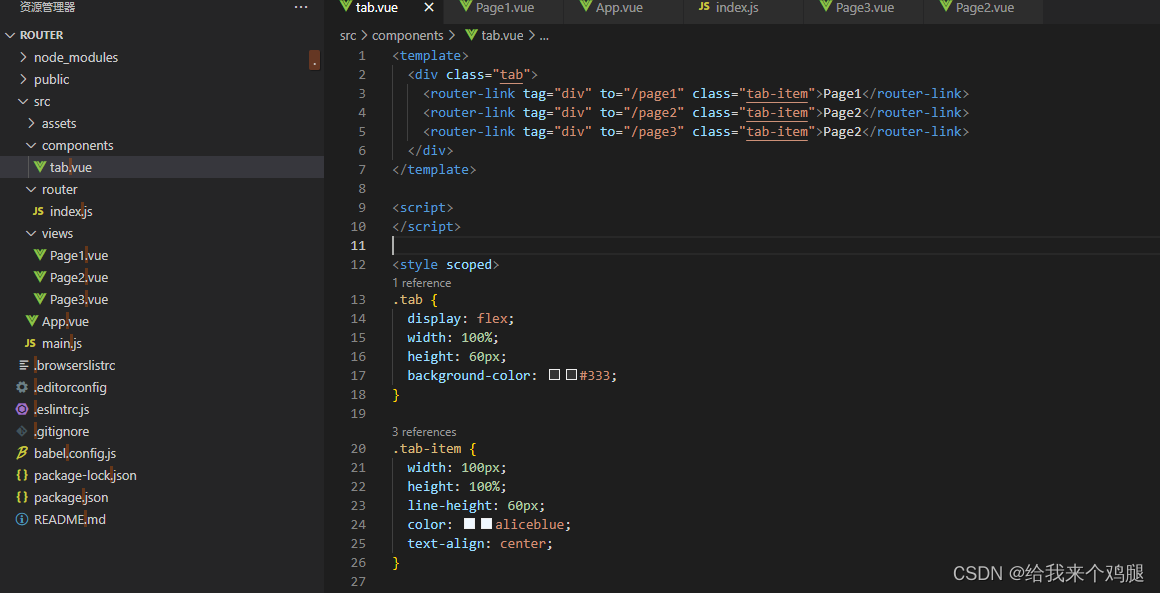
路由-Tab切换页面
Object.entries()

To eliminate air bubbles to save the mushroom h5 small game source code
js半圆环加载进度动画js特效
php - the first of three solid foundations
不错的射击类js小游戏源码

WeChat applet getPhoneNumber interface code=40013
随机推荐
RestTemplate use: set request header, request body
svg实现的树木四季变化
动态组件-component
百日刷题计划 ———— DAY1
WeChat applet getPhoneNumber interface code=40013
package.json and package-lock.json
SQL Server database generation and execution of SQL scripts
嵌入式系统驱动初级【2】——字符设备驱动基础上_基础框架
无线振弦采集仪远程修改参数方式
package.json与package-lock.json
This binding to detailed answers
GCC版本升级到指定版本
Name conventions in FreeRTOS
this的绑定指向详细解答
js半圆环加载进度动画js特效
麻烦问一下,对mysql 场景注入故障,是不是不是对mysql server 端注入故障,只是对ja
MFC入门教程(深入浅出MFC)
鲁大师7月新机性能/流畅榜:骁龙8+正面对决天玑9000+,性能跑分突破123万!
什么是 commonjs2
移动端适配,华为浏览器底色无法正常显示