当前位置:网站首页>Second remaining learning notes
Second remaining learning notes
2022-06-11 07:29:00 【Master. Yi】
level Time Co., LTD. , Only consider p p p Is an odd prime number .
x 2 ≡ n ( m o d p ) x^2\equiv n\pmod p x2≡n(modp)
On secondary surplus
The proof in the link is very good .
determine n ∈ [ 1 , p − 1 ] n\in[1,p-1] n∈[1,p−1] Is it a quadratic residual method : If it doesn't exist x 2 ≡ n ( m o d p ) x^2\equiv n\pmod p x2≡n(modp), be n p − 1 2 ≡ − 1 n^{\frac {p-1}2}\equiv -1 n2p−1≡−1; If there is , be n p − 1 2 ≡ ( n ) p − 1 ≡ 1 n^{\frac {p-1}2}\equiv (\sqrt n)^{p-1}\equiv1 n2p−1≡(n)p−1≡1
x ∈ [ 1 , p − 1 2 ] x\in[1,\frac {p-1}2] x∈[1,2p−1] The square module of each number of p p p Different from each other , x x x And p − x p-x p−x The square module of p p p identical .
yyb!
Add why Find with primitive root x 2 ≡ n ( m o d p ) x^2\equiv n\pmod p x2≡n(modp) Of x x x when , Make g a ≡ n g^a\equiv n ga≡n, If there is a solution , that a a a It must be an even number :
First there is ( g b ) 2 ≡ g 2 b ≡ g a (g^b)^2\equiv g^{2b}\equiv g^a (gb)2≡g2b≡ga, Then there must be 2 b ≡ a ( m o d p − 1 ) 2b\equiv a\pmod {p-1} 2b≡a(modp−1), therefore a a a It must be an even number . It can also be seen that b b b There are two solutions , One is a 2 \frac a2 2a, One is a + p − 1 2 \frac {a+p-1}2 2a+p−1
solution : Random a ∈ [ 0 , p ) a\in[0,p) a∈[0,p), Make w = a 2 − n w=a^2-n w=a2−n, If w w w There is no secondary residue , be ( a + w ) p + 1 2 (a+\sqrt w)^{\frac {p+1}2} (a+w)2p+1 It's a set of solutions , You can put w \sqrt w w Overloaded as imaginary units .
Several important conclusions ( Not in the sense of modulo odd prime numbers 0 term ):
Second surplus * Second surplus = Second surplus
Second surplus * Non quadratic residue = Non quadratic residue
Non quadratic residue * Non quadratic residue = Non quadratic residue
The proof can be obtained by multiplying according to Legendre sign .
So there is a corollary : x ∗ k − 1 x*k^{-1} x∗k−1 It's the second surplus Equivalent to x ∗ k x*k x∗k It's the second surplus .
边栏推荐
- big.js--使用/实例
- C+tinycthread implementation thread
- 421. maximum XOR value of two numbers in the array
- Raspberry pie builds a full-featured NAS server (07): manage your library & read as you please
- [analysis of STL source code] summary notes (3): vector introduction
- 【CF】 A. New Year Candles
- Android and IOS reverse analysis / security detection / penetration testing framework
- [STL source code analysis] summary notes (12): functors and adapters
- The gap between the parent box and the child box
- A case in which the MySQL administrator password cannot take effect
猜你喜欢

软件测试周刊(第75期):唯有平视,才能看见真实的自己。

2022 low voltage electrician operation certificate test question simulation test platform operation

【Oracle 数据库】奶妈式教程day03 排序查询
QObject usage skills -- control function class

webserver

QT interface nested movement based on qscrollarea
Typora set markdown syntax inline mode
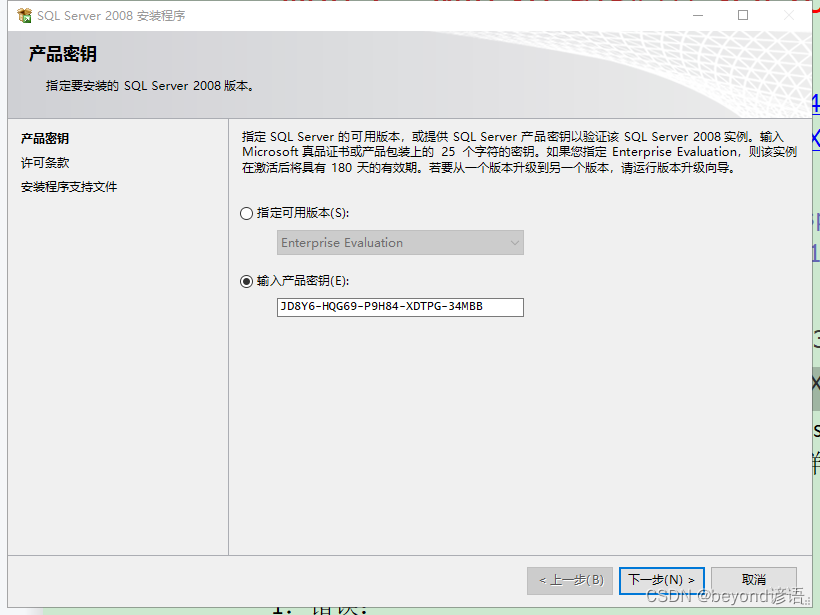
一、SQLServer2008安裝(帶密碼)、創建數據庫、C#窗體項目測試

Mistakes in Niuke JS exercise

Building a full-featured NAS server with raspberry pie (06): built-in file synchronization tool for penetration
随机推荐
Sdl-3 YUV playback
CMAP of Matplotlib
Sqlzoo question brushing record-3
Create a form whose client area is 800 pixels by 600 pixels
MS office level II wrong question record [4]
MS office level II wrong question record [8]
2022年熔化焊接与热切割考试练习题及答案
1、 Sqlserver2008 installation (with password), database creation, C form project test
421. maximum XOR value of two numbers in the array
@JsonProperty注解
【CF#654 (Div. 2)】A. Magical Sticks
Biological sequence intelligent analysis platform blog (1)
一、SQLServer2008安装(带密码)、创建数据库、C#窗体项目测试
2022低压电工考题及在线模拟考试
Shangtang technology has actively resumed work and will vigorously invest in the capacity and deployment of the digital sentry
10 advanced concepts that must be understood in learning SQL
資深OpenStacker - 彭博、Vexxhost昇級為OpenInfra基金會黃金成員
Directrix of ellipse
JVM learning record (VII) -- class loading process and parental delegation model
1442. number of triples forming two exclusive or equal arrays