当前位置:网站首页>【NOI模拟赛】纸老虎博弈(博弈论SG函数,长链剖分)
【NOI模拟赛】纸老虎博弈(博弈论SG函数,长链剖分)
2022-08-04 07:47:00 【DD(XYX)】
题面
某天,C 和 K 觉得很无聊,于是决定玩一个经典小游戏:
在一棵有 n n n 个结点的有根树上,标号为 i i i 的节点上有 a i a_i ai 个棋子。游戏时玩家轮流操作,每次可以将任意一个节点 u u u 上的一个棋子放置到任意一个点 v ∈ U ( u ) v\in U(u) v∈U(u) 上,其中 U ( u ) = s u b t r e e { u } − { u } U(u)=subtree\{u\}-\{u\} U(u)=subtree{ u}−{ u},表示 u u u 的子树内(不包含 u u u 本身)的点组成的集合。不能进行操作者失败。
两人觉得,每个人给自己一个特殊能力可能会比较有趣:
C 在开始游戏之前,可以选择将当前树的树根 R R R 换到与 R R R 相邻的任意一个点 R ′ R' R′ 上。定义两个点相邻当且仅当这两个点有边直接相连。
K 在开始游戏之前,必须选择树上的一个节点,在上面加上一颗棋子。
C 和 K 决定玩 m m m 局游戏。每局游戏的流程如下:
- 游戏开始前,C 和 K 会商量好,先在标号为 x x x 的节点上放上一个棋子,然后将树根设为 y y y。
- 之后 C 可以选择是否发动特殊能力,C 决策完之后 K 可以选择是否发动特殊能力。
- 特殊能力的决策结束后,会在这棵树上进行一局 C 先手、K 后手的游戏。游戏完成后会将树上棋子的状态还原到流程 1 结束后的状态。
由于 C 和 K 都是纸老虎,决策结束后知道谁必胜就够了,不想实际开打 。于是 C 决定考考你:C 在每局游戏的第二步的时候,有多少种决策方式使得不管 K 如何进行特殊能力的操作,开始游戏时都存在必胜策略?两种决策方式不同,当且仅当两种决策更换的树根 R ′ R' R′不同,或者两者中仅有一个没有发动特殊能力。
输入格式
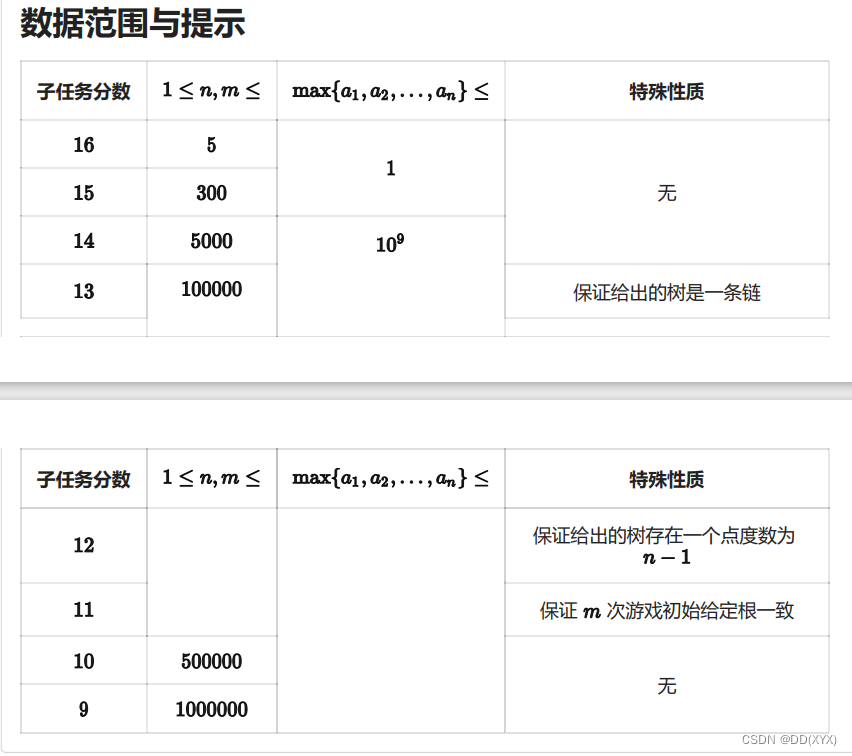
第一行包括一个整数,表示该测试点所在的子任务的分数。你可以使用这个信息判断该测试点满足的特殊性质。特别的,下发样例中此行使用 0 0 0 代替。
第二行包含两个用空格隔开的正整数 n , m n,m n,m,表示树的节点数目以及游戏的轮数。树上的节点从 1 1 1 到 n n n 编号。
接下来 n − 1 n-1 n−1 行,每行包含两个用空格隔开的正整数 u i , v i u_i,v_i ui,vi,满足 1 ≤ u i , v i ≤ n 1\leq u_i,v_i\leq n 1≤ui,vi≤n,表示编号为 u i u_i ui 和 v i v_i vi 的节点之间有边直接相连。
接下来一行包含 n n n 个用空格隔开的整数 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,满足 0 ≤ a 1 , a 2 , . . . , a n ≤ 1 0 9 0\leq a_1,a_2,...,a_n\leq 10^9 0≤a1,a2,...,an≤109。
接下来 m m m 行,每行包含两个用空格隔开的正整数 x , y x,y x,y 描述一局游戏,满足 1 ≤ x , y ≤ n 1\leq x,y\leq n 1≤x,y≤n。
输出格式
你需要输出 m m m 行,其中第 i i i 行应当包含一个非负整数 x x x 表示第 i i i 局游戏中,C 存在多少种使用特殊能力的决策方案,使得 C 在这局游戏中存在必胜策略。注意,不使用特殊能力也是一种可能可行的决策方案。
题解
首先可以归纳得出结论:一棵树根节点放一颗棋子的 SG 函数等于该树的高度。
然后,一个点当根“可行”当且仅当 SG 值大于树高,因为没法通过加一个点让 SG 归零。
于是,暴力方法便是每次修改直接枚举根修改贡献,查询枚举邻接点。
所以我们接下来需要快速修改贡献,以及快速查询邻接点。
我们记录每个点为起点的最长路径和次长路径,会发现无论根在哪,该点的贡献都是最长路径或次长路径,而且贡献为次长路径当且仅当根在最长路径的方向。所以修改只需要支持子树修改。用DFS序+线段树就好。
我们如果对该树进行长链剖分的话,会发现一个点 x x x 的轻儿子为根时树高都是相等的,都等于 x x x 的最长路径+1 。于是,我们只需要用trie树维护所有轻儿子的 SG 值。使用一个整体异或的tag,在子树修改时可以做到 O ( log ) O(\log) O(log) 。
求最长路径和次长路径用换根DP就好了。
总时间复杂度 O ( n log n ) O(n\log n) O(nlogn) ,空间 O ( n log n ) O(n\log n) O(nlogn) 需要节点回收。
CODE
#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN 1000005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
#define UIN unsigned int
#define SQ 317
int xchar() {
static const int maxn = 1000000;
static char b[maxn];
static int pos = 0,len = 0;
if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
if(pos == len) return -1;
return b[pos ++];
}
#define getchar() xchar()
inline LL read() {
LL f = 1,x = 0;int s = getchar();
while(s < '0' || s > '9') {
if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
while(s >= '0' && s <= '9') {
x = (x<<1) + (x<<3) + (s^48);s = getchar();}
return f*x;
}
void putpos(LL x) {
if(!x)return ;putpos(x/10);putchar((x%10)^48);}
inline void putnum(LL x) {
if(!x) {
putchar('0');return ;}
if(x<0) putchar('-'),x = -x;
return putpos(x);
}
inline void AIput(LL x,int c) {
putnum(x);putchar(c);}
int n,m,s,o,k;
int a[MAXN];
int hd[MAXN],nx[MAXN<<1],v[MAXN<<1],cne;
void ins(int x,int y) {
nx[++ cne] = hd[x]; v[cne] = y; hd[x] = cne;
}
struct it{
PR a,b;
it(){
a=b={
0,0};}
}dp[MAXN],dp2[MAXN],pr[MAXN],sf[MAXN];
it merg(it x,it y) {
it z; z.a = max(x.a,y.a);
z.b = max(x.b,y.b);
if(x.a.SE != z.a.SE) z.b = max(z.b,x.a);
if(y.a.SE != z.a.SE) z.b = max(z.b,y.a);
return z;
}
void dfs(int x,int ff) {
dp[x].a = {
0,x};
it p = it();
stack<int> sn;
for(int i = hd[x];i;i = nx[i]) {
if(v[i] != ff) {
dfs(v[i],x);
sn.push(v[i]);
it nm = dp[v[i]];
nm.a.FI ++; nm.a.SE = v[i];
nm.b = {
0,0};
dp[x] = merg(dp[x],nm);
pr[v[i]] = p; pr[v[i]].b = {
0,0};
pr[v[i]].a.SE = x;
p = merg(p,nm);
}
}
p = it();
while(!sn.empty()) {
int y = sn.top(); sn.pop();
sf[y] = p; sf[y].b = {
0,0};
sf[y].a.SE = x;
it nm = dp[y]; nm.a.FI ++;
nm.a.SE = y; nm.b = {
0,0};
p = merg(p,nm);
}
return ;
}
int fa[MAXN];
int tre[MAXN<<2],M;
void maketree(int n) {
M=1; while(M<n+2) M<<=1;
}
void addseg(int l,int r,int y) {
for(int s=M+l-1,t=M+r+1;(s>>1)^(t>>1);s >>= 1,t >>= 1) {
if(!(s&1)) tre[s^1] ^= y;
if(t & 1) tre[t^1] ^= y;
} return ;
}
int findp(int x) {
int as=0,s=M+x;
while(s)as^=tre[s],s>>=1;
return as;
}
int dfn[MAXN],rr[MAXN],tim;
void dfs2(int x,int ff) {
fa[x] = ff;
dp2[x].a = {
0,x};
if(ff) {
dp2[x] = merg(dp2[ff],merg(pr[x],sf[x]));
dp2[x].a.FI ++; dp2[x].a.SE = ff;
dp2[x].b = {
0,0};
}
dp[x] = merg(dp[x],dp2[x]);
dfn[x] = ++ tim;
for(int i = hd[x];i;i = nx[i]) {
if(v[i] != ff) {
dfs2(v[i],x);
}
}
rr[x] = tim;
return ;
}
int tri[MAXN*25][2],ct[MAXN*25];
stack<int> tra; int cnt = 1;
int newp() {
if(tra.empty()) tra.push(++ cnt);
int x = tra.top(); tra.pop();
tri[x][0]=tri[x][1]=ct[x]=0;return x;
}
void ins(int p,int x,int y) {
static int st[55],tp;
st[tp = 0] = p;
for(int i = 20;i >= 0;i --) {
int d = (x>>i)&1;
if(!tri[p][d]) tri[p][d] = newp();
p = tri[p][d]; ct[p] += y;
st[++ tp] = p;
}
while(tp > 0 && ct[st[tp]] == 0) {
int t = st[tp --];
int ff = st[tp];
if(tri[ff][0] == t) tri[ff][0] = 0;
if(tri[ff][1] == t) tri[ff][1] = 0;
tra.push(t);
} return ;
}
int cont(int p,int x,int y) {
int as = 0;
for(int i = 20;i >= 0;i --) {
int d = (x>>i)&1,d2 = (y>>i)&1;
if(!d2) as += ct[tri[p][d^1]];
p = tri[p][d^d2];
} return as;
}
int sm[MAXN],mxd[MAXN],hv[MAXN],rt[MAXN];
void xorp(int x,int y) {
if(!x) return ;
int ff = fa[x];
if(ff && x != hv[ff]) {
int nm = sm[x] ^ findp(dfn[x]) ^ findp(dfn[ff]);
ins(rt[ff],nm,-1);
ins(rt[ff],nm^y,1);
}
sm[x] ^= y;
return ;
}
void xortree(int x,int y) {
if(!x) return ;
int ff = fa[x];
if(ff && x != hv[ff]) {
int nm = sm[x] ^ findp(dfn[x]) ^ findp(dfn[ff]);
ins(rt[ff],nm,-1);
ins(rt[ff],nm^y,1);
}
addseg(dfn[x],rr[x],y);
return ;
}
void addpoint(int x) {
if(hv[x] == fa[x]) {
xortree(1,dp[x].b.FI);
xortree(x,mxd[x]^dp[x].b.FI);
}
else {
xortree(1,mxd[x]);
xortree(hv[x],mxd[x]^dp[x].b.FI);
} return ;
}
bool checkp(int x) {
int nm = sm[x] ^ findp(dfn[x]);
return nm > mxd[x];
}
int main() {
freopen("classic.in","r",stdin);// “典”
freopen("classic.out","w",stdout);
int pts = read();
n = read(); m = read();
for(int i = 1;i < n;i ++) {
s = read();o = read();
ins(s,o); ins(o,s);
}
for(int i = 1;i <= n;i ++) {
a[i] = read()&1;
}
dfs(1,0); dfs2(1,0);
maketree(n);
for(int i = 1;i <= n;i ++) mxd[i] = dp[i].a.FI,hv[i] = dp[i].a.SE,rt[i] = newp();
for(int i = 1;i <= n;i ++) {
if(fa[i] && i != hv[fa[i]]) {
ins(rt[fa[i]],0,1);
}
}
for(int i = 1;i <= n;i ++) {
if(a[i]) {
addpoint(i);
}
}
for(int i = 1;i <= m;i ++) {
s = read();o = read();
addpoint(s);
int ans = 0,nm = findp(dfn[o]);
if((sm[o]^nm) > mxd[o]) ans ++;
ans += cont(rt[o],nm,mxd[o]+1);
if(hv[o]) ans += checkp(hv[o]);
if(fa[o] && fa[o] != hv[o]) ans += checkp(fa[o]);
AIput(ans,'\n');
}
return 0;
}
边栏推荐
猜你喜欢
全国职业院校技能大赛网络安全竞赛之应急响应

沃尔玛、阿里国际该如何做测评自养号?
小程序如何使用订阅消息(PHP代码+小程序js代码)

此时已莺飞草长,愿世间美好与你环环相扣
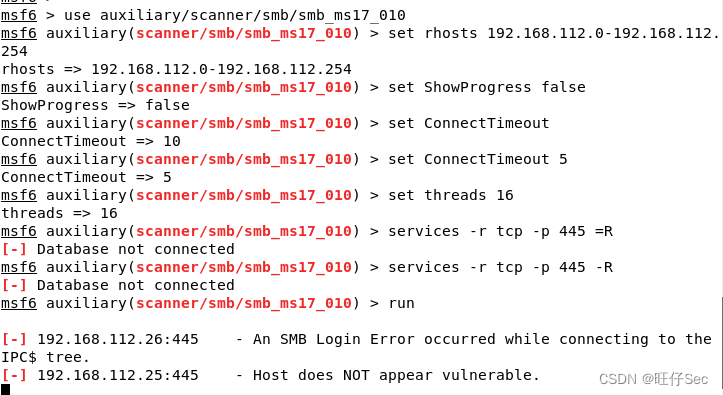
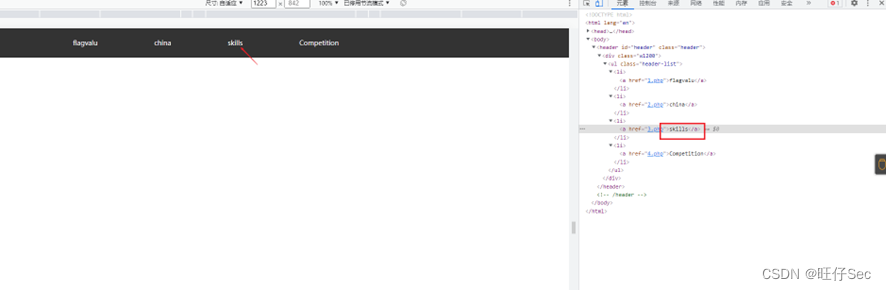
Secondary network security competition C module MS17-010 batch scanning

两日总结五

dalle:zero-shot text-to-image generation

The national vocational skills contest competition of network security emergency response
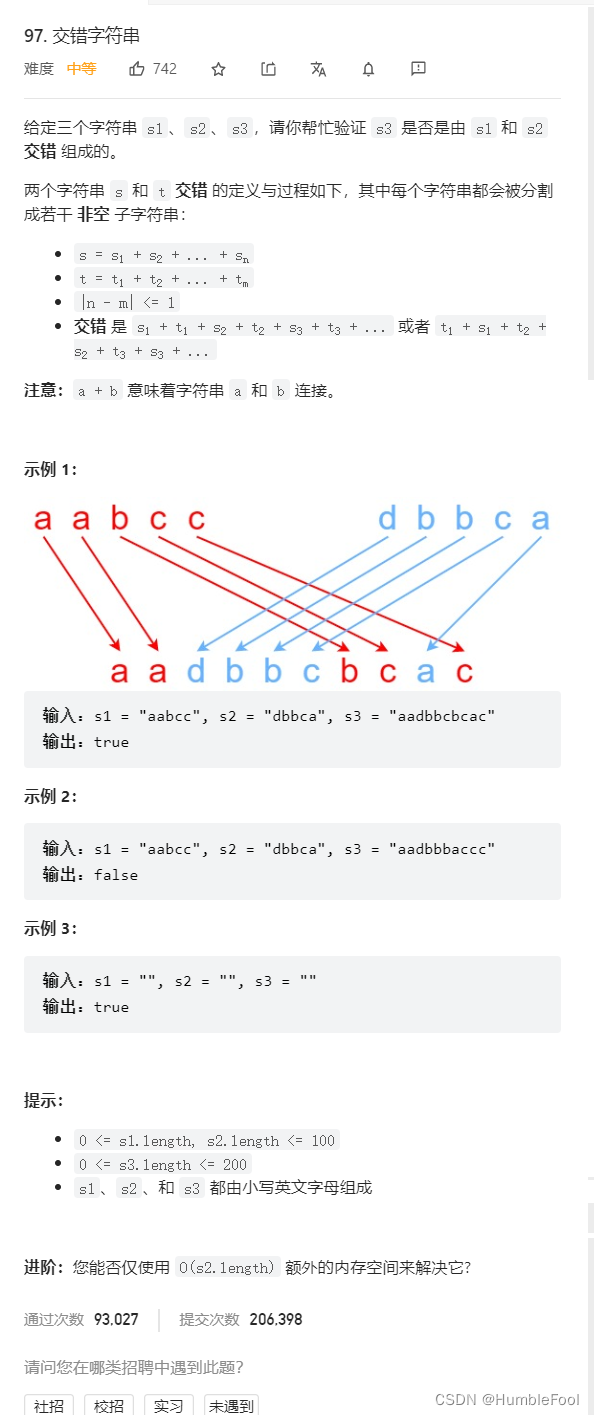
LeetCode 97. 交错字符串
![玩转TypeScript对象、对象作为参数进行函数传递、接口和内置对象[无敌态]](/img/23/3405b488d11a4700a9b47758214574.png)
玩转TypeScript对象、对象作为参数进行函数传递、接口和内置对象[无敌态]
随机推荐
dalle:zero-shot text-to-image generation
实现加载驱动、得到数据库对象、关闭资源的代码复用,将代码提取到相应的工具包里边。优化程序
[Paper Notes] - Low Illumination Image Enhancement - Supervised - RetinexNet - 2018-BMVC
MotionLayout的使用
JNI学习1.环境配置与简单函数实现
【UE虚幻引擎】UE5三步骤实现AI漫游与对话行为
金仓数据库KingbaseES客户端编程接口指南-JDBC(8. JDBC 元数据处理)
千万级别的表分页查询非常慢,怎么办?
字节跳动岗位薪酬体系曝光,看完我真的酸了...
给Unity Behavior Designer(Unity行为树) 的Can See Object 画圆锥辅助图
Cross-species regulatory sequence activity prediction
powershell和cmd对比
中职网络安全竞赛B模块新题
卷积神经网络CNN
开发小技巧 navicate如何点击单元格显示全部的文本内容或通过图像查看内容
七牛云上传图片和本地上传
轻量化Backbone VGNetG成就“不做选择,全都要”轻量化主干网络
IntelliJ新建一个类或者包的快捷键是什么?
登录拦截实现过程
【字符串】最小表示法