Solution and analysis of Hanoi Tower problem

One 、 Introduction of recursive algorithm

         This article is about an ancient and classic Hanoi Tower problem , It is a good application example of recursive algorithm . Introduction to recursive functions , stay Use recursive functions to solve the inverse problem of strings The article introduces . The idea of recursion is to solve computable problems , His fundamental feature is the gradual calculation and decomposition of this calculation , By decomposing a big problem into logically identical small problems , Then solve the small problem and get the final answer . Programs that use recursive algorithms are often concise in form , This is where his value lies .（ Better reading experience , Please visit Programmers are on the road ）
　　 Computers use stack memory structures to physically implement recursive algorithms , Every recursive call , The system should return the return address of this call 、 local variable 、 Formal parameters are pressed into the stack equivalently , At the end of the call , Then take the saved information from the top of the stack and return it to the corresponding variable and exit the stack , Then continue to execute the recursive upper function . Because the stack space allocated by the computer system to each program is limited , therefore , When using recursion to solve problems , Be sure to pay attention to the depth of recursion , If the number of recursion is too many , Stack overflow is likely to occur , Cause problem solving failure .

Two 、 The hanotta problem

2.1 Origin of the problem

It's said that in the ancient temple of India , There is one called the Hanoi Tower (Hanoi) The game of . The game is on a copper device , There are three rods ( Number A、B、C), stay A From the bottom up 、 Place in order from large to small 64 A gold plate . The goal of the game ： hold A All the gold plates on the pole are moved to C On the pole , And still keep the original order . Operating rules ： Only one plate can be moved at a time , And keep the big plate down all the time during the moving process , Small in , The plate can be placed during the operation A、B、C On any pole .

2.2 Problem analysis

         The tower of Hanoi problem is a multi branch recursive solution , Relative to the recursive solution of single branch （ Such as ： Recursive solution of factorial ） Come on , It's not easy to understand , But as long as we grasp the core of recursion, we can understand the logic of this program . There are three steps in the solution of Hanoi Tower ：

1） hold N-1 null Move to the transfer column
2） The first N The plates move to Target column
3） Put the above of the transfer column N-1 With the help of the currently free pillars Move to Target column .

         Be careful , The upper transfer column , Starting column , It will change . The logic of recursion at every level is , With the help of " Target pillars ", take n-1 individual The plate moves to “ Transfer column ”, Then move the last plate to " Target pillars ", Then move the plates on the transfer column to " Target pillars ".
　　 No matter how many plates there are , In the process of moving , Follow the above three steps . On mobile page N When it's a plate , We have to find a way to put the front N-1 Move the plates to the transfer column , Only then can the N Move a plate to the target column . On mobile page N-1 When it's a plate , It's also necessary to put the front N-2 Move the plates to the transfer column , Then we can put the N-1 Move a plate to the target column . therefore , You can see , Move N、N-1、N-2··· The idea from plate No. 1 to the target column is the same , therefore , We can solve this problem with recursion .

2.3 Program realization

#include<stdio.h>

void hnt(int n, char a,  char b, char c){
    

   if(n == 1){
       //  Recursive out of bounds condition 
   
   	printf("%c -- > %c \n", a,c); 
   }else{
    
   	/*  The logic of recursion at every level is , With the help of " Target pillars ", take n-1 individual   The plate moves to  " Transfer column ", Then move the last plate to " Target pillars ".  Be careful , The transfer column here will change . */
   	hnt(n-1,a,c,b); // ①  With the help of  c  Pillar will a On the pillar n-1 null   Move to  b  On the pillars 

   	printf("%c -- > %c \n", a,c); // ②  take  a The first one on the post n null   Move to  c On the pillars 

   	hnt(n-1, b,a,c);  // ③  Will be in b On the pillar n-1 null , With the help of  a  column （ here a Free ）  Move to  c  On the pillars 
   }
}

int main(){
    
   int n;
   scanf("%d", &n);
   hnt(n,'a','b','c');
   return 0;
}

2.4 Program analysis

         Through the analysis of the tower of Hanoi , You may understand , The above program is the answer to the problem , But you may have some doubts , Why the above program , You can record the moving process of each step ？ For this multi branch recursive algorithm , If you understand single branch recursion , List the moving process of each step in your mind as much as possible , Sometimes it's very difficult , This is also inconsistent with the principle of using recursion to solve problems . But if we really want to understand the specific process of each step , What shall I do? ？ The following is a summary , To list N∈[1,4] The moving process of , Analyze his movement law .
　　 When N =1 when ：

　　 When N =2 when ：

　　 When N =3 when ：
　　 adopt N=1,N=2 The solution of , We can infer that ,N =3 When , There will be 3 + 1 + 3 = 7 Secondary mobility .3 A plate , We have to move the first two plates to B, Then move the third plate to C, Finally, put B Two plates on top , With the help of A Move to C. Two plates on top , First move to B, Then move to C, These two processes , The number of moves required is the same , The same goes for mobile logic .

　　 When N =4 when ：
　　 Or the previous logic ,N=4 When , There will be 7 + 1 + 7 = 15 Secondary mobility . The idea is the same as before , The former 3 null , With the help of C Move to B, Then move the fourth plate to C.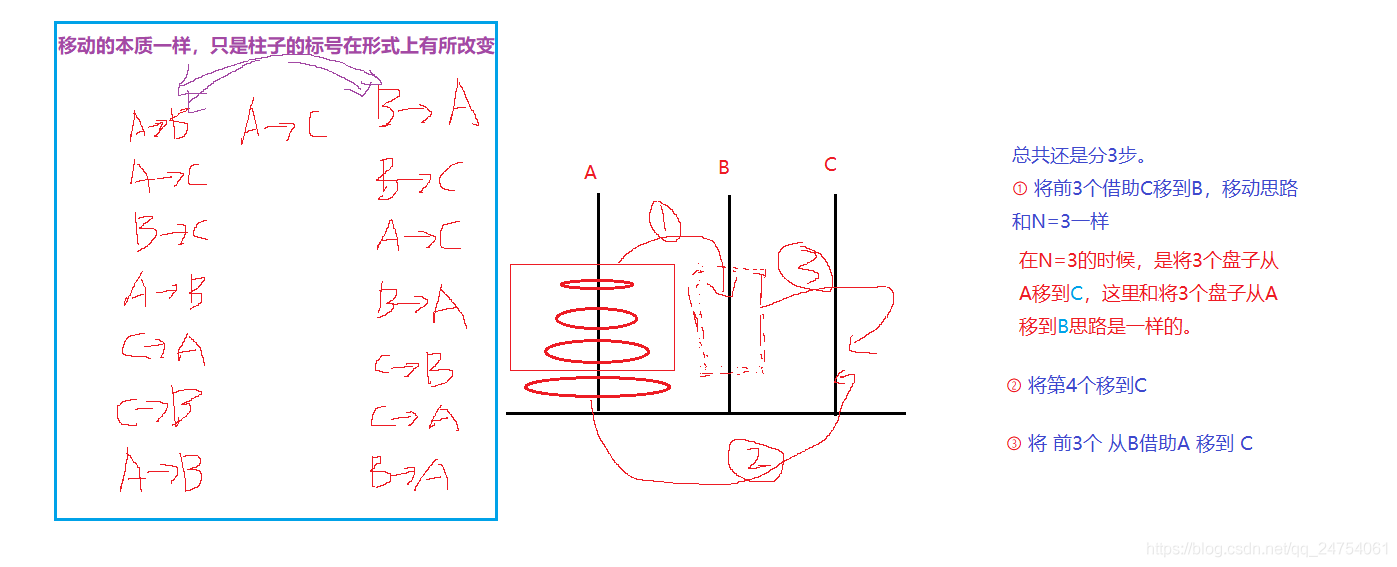

         We can see from the previous demonstrations , solve N And solve N-1 Their ideas are exactly the same , This is the core to ensure that recursive algorithms can be used .
　　A、B、C Just a formal annotation , In essence, the above meaning is , start 、 transit 、 The goal is . In the process of moving , If you want to ensure that the small one is on , Big next , We have to rely on transit , To achieve , As for who is the transit , This sum （N-1） This pile of plates is related to the location .
　　 When writing recursive programs , The points needing attention are shown in the following figure ：

3、 ... and 、 summary

         The core of recursive algorithm is recursive logic , therefore , Use recursive algorithm to solve the problem , We don't have to worry about the specific operation of each layer of function , And put the core on logic , If the solution of the problem is inductive , There is a recursive relationship in it , And it is computable , Then there is no logical problem , Generally, recursive algorithm can be used to solve .
　　 Recursion includes single branch recursion and multi branch recursion , Single branch is relatively simple to understand , For example, the following recursive program

int f(int n) // seek n The factorial
{
　　int fac;
　　if (n == 0 || n == 1)
　　　　fac = 1;
　　else
　　　　fac = f(n - 1) * n;
　　return fac;
}

         Multi branched, such as tower of Hanoi 、 Binary tree traversal, etc , It's more difficult to understand , But the mind is the same .
　　 When a computer executes a recursive program , Calls to functions at each level , Stack data structure is used for on-site protection , So when writing recursive programs , Pay attention to the depth of recursion , Prevent emergence Stack Overflow abnormal .