当前位置:网站首页>【动态规划】—— 背包问题
【动态规划】—— 背包问题
2022-06-27 12:36:00 【玄澈_】

背包问题的分类

01背包问题
输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
8
在求选 第 i 个物品的状态转移方程的时候,我们可以取出 ![\small f[i-1,j-v[i]]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_14.gif) 的最大值再加上 w[i]
的最大值再加上 w[i]
不选第 i 个物品的话,状态转移方程就是 ![\small f[i][j] = f[i - 1,j]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_11.gif)
![\small f[i,j]=max\begin{cases}f[i-1,j] & \\ f[i-1, j -V_i] +w_i &if(j\geqslant V_i) \end{cases}](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_6.gif)
![\small f[i]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_21.gif)

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ )
for(int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}从二维优化到一维
通过 DP 的状态转移方程,我们发现,每一阶段的 i 的状态只与上一阶段的 i-1 的状态有关。在这种情况下,可以使用称为“滚动数组”的优化方法,降低时间开销。
因为 ![\small f[j] = max(f[j], f[j - v[i]] + w[i])](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_19.gif) 这里的
这里的 ![\small f[j - v[i]]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_31.gif) 一定比
一定比 ![\small f[j]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_39.gif) 更早计算出来,所以
更早计算出来,所以 ![\small f[j - v[i]]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_31.gif) 计算得到的是第 i 层的,而在我们上述的 DP 方程中,所用的是第 i - 1 层的数据,所以如果是从小到大遍历体积的话,会出现“数据污染” 的情况。所以体积的枚举要从大到小来枚举。
计算得到的是第 i 层的,而在我们上述的 DP 方程中,所用的是第 i - 1 层的数据,所以如果是从小到大遍历体积的话,会出现“数据污染” 的情况。所以体积的枚举要从大到小来枚举。
一维优化代码实现
#include <iostream> #include <cstring> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N]; int main() { cin >> n >> m; for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i]; for(int i = 1; i <= n; i ++ ) for(int j = m; j >= v[i]; j -- ) { f[j] = max(f[j], f[j - v[i]] + w[i]); } cout << f[m] << endl; return 0; }
完全背包问题
输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
10
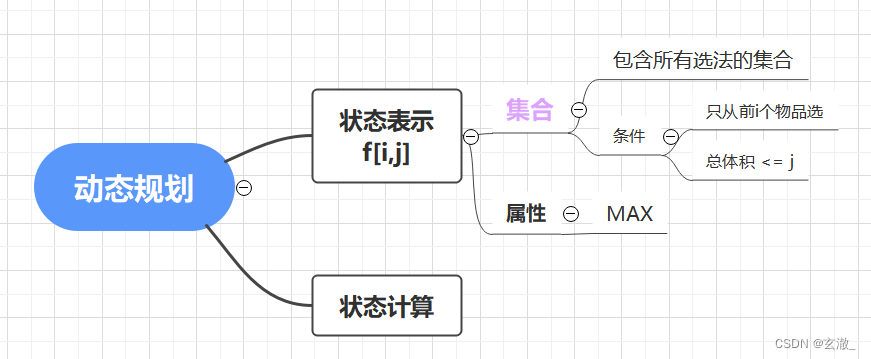
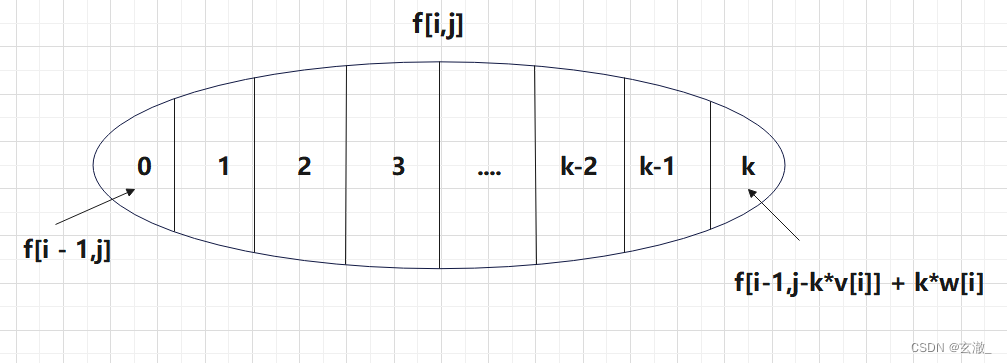
对于朴素做法有: ![\small f[i,j]=f[i,j-k*v[i]]+k*w[i]](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_24.gif) 类比01背包问题
类比01背包问题
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ )
for(int j = 0; j <= m; j ++ )
for(int k = 0; k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[n][m] << endl;
return 0;
}通过比较下列等式可以发现:
得到:
![\large {\color{Red} f[i,j] = max(f[i - 1,j], f[i, j - v] + w)}](//img.inotgo.com/imagesLocal/202206/27/202206271235354600_22.gif)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ )
for(int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}一维优化
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N]; int main() { cin >> n >> m; for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i]; for(int i = 1; i <= n; i ++ ) for(int j = v[i]; j <= m; j ++ ) { f[j] = max(f[j], f[j - v[i]] + w[i]); } cout << f[m] << endl; return 0; }
对比01背包和完全背包问题,有以下差异 :
01背包:![f[i,j] = max(f[i,j], f[i - 1][j-v[i]] + w[i])](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_40.gif)
完全背包:![f[i,j]=max(f[i,j],f[i][j - v[i]+ w[i])](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_15.gif)
对于完全背包来说,体积的枚举可以从 v[i] 枚举到 m,因为它每 i 层的更新使用的是第 i 层的数据,不存在“数据污染”的问题。
多重背包问题
输入样例
4 5 1 2 3 2 4 1 3 4 3 4 5 2输出样例:
10
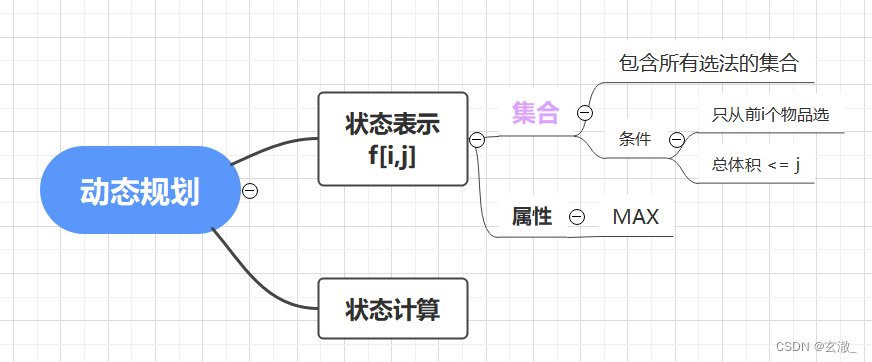

![f[i,j]=max(f[i-1][j-v[i] * k] + w[i] * k)](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_29.gif)
朴素写法
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];
for(int i = 1; i <= n; i ++ )
for(int j = 0; j <= m; j ++ )
for(int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}多重背包的二进制优化
众所周知,从  这 k 个2的整数次幂中选出若干个相加,可以表示出
这 k 个2的整数次幂中选出若干个相加,可以表示出  之间的任意整数。进一步的,我们求出满足
之间的任意整数。进一步的,我们求出满足  的最大整数 p,设
的最大整数 p,设 那么:
那么:
- 根据 p 的最大性,有
 ,可推出
,可推出  ,因此
,因此  选出若干个相加可以表示出
选出若干个相加可以表示出  之间的任意整数;
之间的任意整数; - 从
 中选出若干个相加,可以表示出
中选出若干个相加,可以表示出  之间的任何整数,而根据 Ri 的定义,
之间的任何整数,而根据 Ri 的定义,  ,因此,
,因此, 选出若干个可以表示出
选出若干个可以表示出 之间的任意整数。
之间的任意整数。
综上所述,我们可以把数量为  的第 i 个物品拆成 p + 2个物品,他们的体积分别为:
的第 i 个物品拆成 p + 2个物品,他们的体积分别为:

这 p + 2 个物品可以凑成  之间所有能被Vi整除的数,并且不能凑成大于 Ci * Vi 的数。这等价于原问题中体积为 Vi 的物品可以使用 0~Ci 次。该方法仅将每种物品拆分成了
之间所有能被Vi整除的数,并且不能凑成大于 Ci * Vi 的数。这等价于原问题中体积为 Vi 的物品可以使用 0~Ci 次。该方法仅将每种物品拆分成了  个,效率较高。
个,效率较高。
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 25000, M = 2010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
int cnt = 0;
for(int i = 1; i <= n; i ++ )
{
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while(k <= s)
{
cnt ++ ;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if(s > 0)
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for(int i = 1; i <= n; i ++ )
for(int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}分组背包问题
输入样例
3 5 2 1 2 2 4 1 3 4 1 4 5输出样例:
8


AC代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
{
cin >> s[i];
for(int j = 0; j < s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for(int i = 1; i <= n; i ++ )
for(int j = m; j >= 0; j -- )
for(int k = 0; k < s[i]; k ++ )
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}边栏推荐
猜你喜欢

ACL 2022 | TAMT proposed by Chinese Academy of Sciences: TAMT: search for a portable Bert subnet through downstream task independent mask training

Sword finger offer 04 Find in 2D array

让学指针变得更简单(一)

Industry insight - how should brand e-commerce reshape growth under the new retail format?

今晚战码先锋润和赛道第2期直播丨如何参与OpenHarmony代码贡献

DM8:达梦数据库-锁超时

【医学分割】unet3+

An interesting experiment of netmask
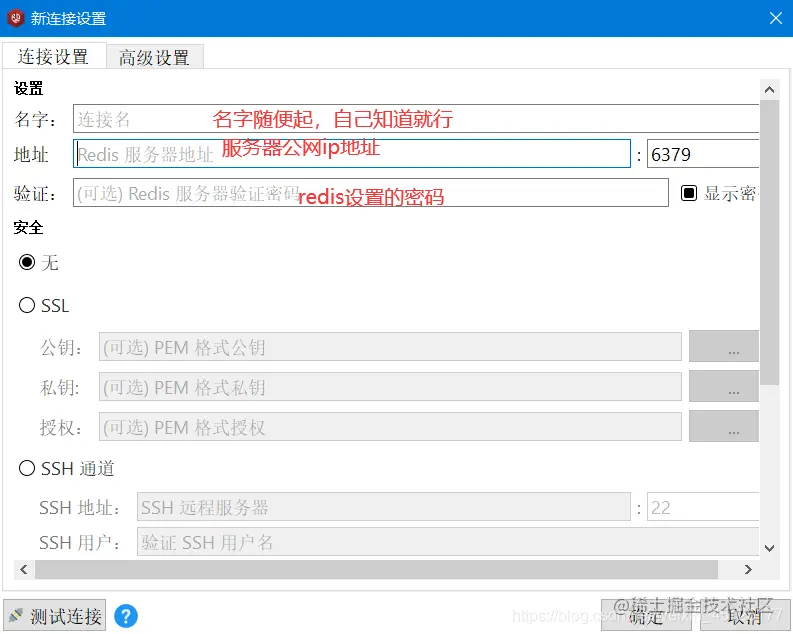
Local visualization tool connects to redis of Alibaba cloud CentOS server

微服务拆分
随机推荐
让学指针变得更简单(二)
Interview shock 60: what will cause MySQL index invalidation?
数据库的复习总结
Microservice splitting
数据库系列:MySQL索引优化与性能提升总结(综合版)
OpenFeign服务接口调用
First encounter with dynamic programming
An interesting experiment of netmask
How to close windows defender Security Center
Minimum editing distance (linear DP writing method)
Review summary of database
Object serialization
Snipaste, the world's strongest screenshot software
ssh服务器配置文件sshd_config 及操作
浏览器输入url地址,到页面渲染发生了什么
Pyqt, pyside slot functions are executed twice
【粉丝福利】今天给大家介绍一个白捡钱的方法-可转债,本人亲自验证,每年每人能获利1500元
GCC compiling dynamic and static libraries
推荐系统的下一步?阿里时空聚合GNN,效果吊打LightGCN!
gcc编译动态库和静态库


![\small f[i,j] = max(f[i -1,j],f[i-1,j-v]+w,f[i-1,j-2v]+2w\cdots )](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_38.gif)
![\small f[i,j-v]=max( f[i-1,j-v],f[i-1],f[i-1,j-2v]+w,f[i-2,j-3v]+2w\cdots )](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_3.gif)
![\large {\color{Red} f[i,j] = max(f[i - 1,j], f[i, j - v] + w)}](http://img.inotgo.com/imagesLocal/202206/27/202206271235354600_22.gif)

 ,可推出
,可推出  ,因此
,因此  选出若干个相加可以表示出
选出若干个相加可以表示出  之间的任意整数;
之间的任意整数; 中选出若干个相加,可以表示出
中选出若干个相加,可以表示出  之间的任何整数,而根据 Ri 的定义,
之间的任何整数,而根据 Ri 的定义,  ,因此,
,因此, 选出若干个可以表示出
选出若干个可以表示出 之间的任意整数。
之间的任意整数。