Connectivity basis of Graphs

One   Connectivity of undirected graphs

In the undirected graph , If from node vi To the node vj There is a path , Then it is called node vi And nodes vj It's connected . If any two nodes in the graph are connected , A graph is called a connected graph . The following figure is a connected graph .

Undirected graph G The polar Dalian Tong subgraph of becomes a graph G The connected component of . Polar Dalian tongsubgraph is a graph G Connected subgraphs , If you add another node , Then the subgraph is not connected . The connected component of a connected graph is itself ; An unconnected graph has more than two connected components .

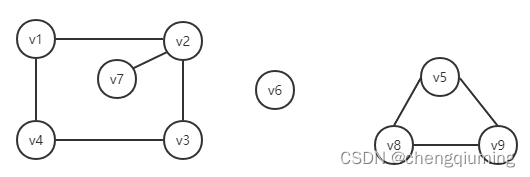
for example , Below is a picture of 3 Connected components

Two   Connectivity of directed graphs

In a directed graph , If any two nodes in the graph start from vi To vj All have paths , And from vj To vi There are also paths , It's called a picture G It's a strongly connected graph .

Directed graph G The polar Dalian Tongzi graph of is called G The strong connected component of . A maximal strongly connected subgraph is a graph G Strong connected subgraphs of , If you add another node to the graph , Then the subgraph is no longer strongly connected 、

The following figure ,a Graph is strongly connected ,b It's not a strongly connected graph ,c yes b The strong connected component of .

3、 ... and   Bridges and cut points of undirected graphs

The bridge is the traffic artery connecting the two banks of the river , The bridge is broken , Then the two banks of the river are no longer connected . In the picture , Bridges have the same meaning , As shown in the figure below , Get rid of 5-8  after , The graph is split into two disconnected subgraphs , edge 5-8  Figure  G  The bridge of , Again , edge 5-7  Also figure  G  The bridge of .

If we remove the undirected connected graph G One of the sides e after , chart G Split into two disjointed subgraphs , that e Figure G A bridge or cut edge .

In the daily network, there are many routers to connect the network , It doesn't matter if some routers are broken , The network is still connected , But if critical router breaks down , Then the network will no longer be connected . As shown in the figure below , If node 5 Your router is broken , chart G Will no longer be connected , Will split into 3 Disjoint subgraphs , The node 5 It's called graph G The cutting point of .

If we remove the undirected connected graph G A point in v And v After all associated edges , chart G Splitting into two or more disjointed subgraphs , that v Figure G The cutting point of .

Be careful ： When deleting an edge , Just delete the edge , Do not delete points associated with edges ; When deleting a cut point , To delete this point and all its associated edges .

The relationship between the cut point and the bridge ： A cut point does not necessarily have a bridge , There must be a cutting point if there is a bridge , The bridge must be the edge to which the cutting point is attached .

Four   The biconnected components of an undirected graph

If there is no bridge in an undirected graph , It is called edge biconnected graph . In edge biconnected graphs , There are two or more paths between any two points , And the edges on the path do not repeat each other .

If there is no cut point in an undirected graph , It is called a dot biconnected graph . In a vertex biconnected graph , If the number of nodes is greater than 2, Then there are two or more paths between any two points , And the points on the path do not repeat each other .

The maximal biconnected subgraphs of an undirected graph are called edge biconnected components . The maximal vertex biconnected subgraph of an undirected graph is called vertex biconnected . Both are collectively referred to as doubly connected components .

5、 ... and   Contraction point of doubly connected components

Treat each edge biconnected component as a point , Think of the bridge as an undirected edge connecting two contraction points , You can get a tree , This method is called e-DCC Shrinkage point .

for example , In the figure below, there are two bridges ：5-7 and 5-8, Keep the edges of each bridge , Keep the edges of each bridge , The edge biconnected components at both ends of the bridge are reduced to a point , Make a tree .

Be careful ： Edge biconnected components are the connected blocks left after deleting the bridge , But the point double connected component is not the connected block left after deleting the cut point .

In the figure G There are two cut points in （5 and 8） And 4 Point connected components , As shown in the figure below .

Make every point doubly connected v-DCC All as a point , Regard the cut point as a point , Each cut point contains its v-DCC Connect an edge , Get a tree , This method is called v-DCC Shrinkage point .

for example , In the figure  G  There are two cut points in 5 and 8, front 3 The two dot biconnected components all contain 5, So from 5 Lead an edge to them , The last two point biconnected components contain 8, So from 8 Lead an edge to them .