当前位置:网站首页>Some coding tips
Some coding tips
2022-06-10 13:14:00 【51CTO】
recursion control
How to prove the correct execution of recursive functions ?
- Mathematics in mathematical induction / Natural language <--> Programming language
Recursive writing method
- Strictly define the function of recursive function , Including the parameters , Return value ,Side-effct
- First commonly , after special
- Each call must narrow The scale of the problem
- The scale of each problem must be reduced to 1
Linked list creation
Head -->1-->2-->3-->4-->5-->null
Why do you like to ask a linked list in an interview ( A one-way )
- Easy to understand
- The code is hard to write
- Examine the code's ability through the linked list itself
List reversal
List all combinations (side effect)
- combinations([1, 2, 3, 4], 2):
- [1, 2]、[1、3]、[1、4]、[2、3]、[2、4]、[3、4]
Recursive disadvantage :
- Function call overhead
- stack overflow
- The scale of the problem :n million Stack size
Cycle control
recursive --> Non recursive
- The generalized approach still requires the use of stacks
- Complex code , Don't solve the problem fundamentally
Loop invariants (loop invariant)
- Is an assertion that defines the conditions that each variable satisfies
-
Var a, b; -
While(){
}
Circular writing method
- Define loop invariants , And keep the loop invariant after each end of the loop body
- First general , Post special
- Each time you must advance the value of the variable involved in the loop invariant
- The scale of each push must be 1
List reversal
In the list delete_if
- duplicate removal
- The header node has no previous What do I do ?
- Special treatment
- Add virtual head node
Boundary control
for example : Two points search Find elements in a binary array k, return k The subscript binarySearch([1, 2, 10, 15, 100], 15) == 3
Binary search ideas :
- Specify the value to find k Possible array in arr Inner subscript interval a, b
- Calculation interval a,b In the middle m
- if k<arr[m], Reduce the interval to a, m. Go ahead with the binary search
- if k>arr[m], Reduce the interval to m, b. Go ahead with the binary search
data structure
Trees -- Key points and difficulties
Write a program on the whiteboard : Whiteboard 、 paper and pen 、Word file 、 Notepad Inconvenient to modify ; Indenting is inconvenient ; Alignment difficulties
There is no conflict in my heart ;
Think before you write ;
Don't be afraid to revise / rewrite
review
list :
- Array -- Random access
- Linked list
- queue 、 Stack -- Pay attention to the interview
Trees :
- Binary tree
- Search tree
- Pile up / Priority queue
Stack / queue / Priority queue
Map<K, V> / Set<K>
- HashMap / HashSet --> K.hashCode()
- TreeMap / TreeSet -- > K implements Comparable
chart :
- Undirected graph
- Directed graph
- Directed acyclic graph
- Graph algorithm -- complex , Generally, no algorithm questions are given in the interview
- Depth-first traversal
- Breadth first traversal
- A topological sort
- Shortest path / Minimum spanning tree
Mathematical induction -- Used in coding
Used to prove that assertions hold true for all natural numbers
- To prove to N=1 establish
- prove N>1 when : If for N-1 establish , So for N establish
The law of mathematical induction : verification :1+2+3+4+...+n=n(n+1)/2
- 1 = 1*2/2
- If 1+2+3+...+(n-1) = (n-1)n/2
- that 1+2+3+...+n = 1+2+3+...+(n-1)+n=(n-1)n/2+n = (n(n-1)+2n)/2=n(n+1)/2
边栏推荐
- Development trend of Web Development
- Timeline and logistics information. You don't need stepview at all
- 【FAQ】运动健康服务REST API接口使用过程中常见问题和解决方法总结
- CMakeLists. Txt how to write
- JS prohibit copying page content
- 【FLinlk】Flink小坑之kerberos动态认证
- Tidb elementary course experience 8 (cluster management and maintenance, adding a tikv node)
- CMakeLists.txt 如何编写
- Shi Yigong and other teams posted on the cover of Science: AI and freeze electron microscope revealed the structure of "atomic level" NPC, a breakthrough in life science
- QT database application 22 file coding format recognition
猜你喜欢
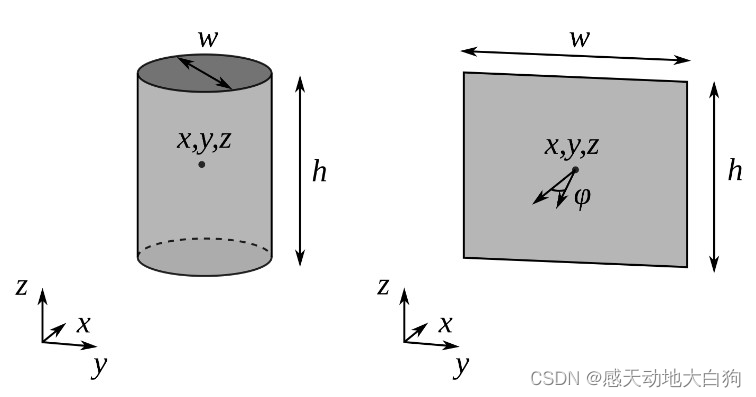
Automatic Mapping of Tailored Landmark Representations for Automated Driving and Map Learning 论文阅读

Google proposed the super pre training model coca, and the accuracy of fine-tuning top-1 on Imagenet reached 91%! SOTA on multiple downstream tasks!

Final exam - Principles of compilation

IQR box diagram

Alibaba cloud ECS server builds MySQL database
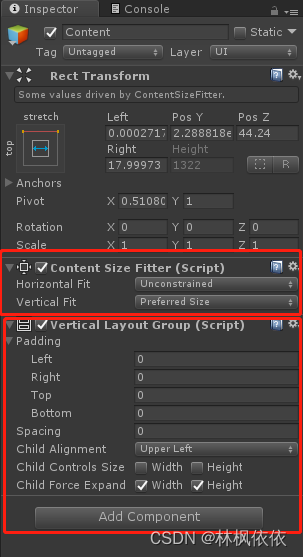
Unity typewriter to automatically roll text to the bottom of the text box

Count the number and average value of natural numbers whose sum of bits within 100 is 7

Qt数据库应用22-文件编码格式识别

蔚来:“拿捏”了数据,“扭捏”着未来

DynaSLAM II: Tightly-Coupled Multi-Object Tracking and SLAM 论文阅读
随机推荐
How to write code that is not easy to overflow memory
TIDB 初级课程体验 8 (集群的管理维护, 添加一个TIKV节点)
Qt数据库应用22-文件编码格式识别
Can qiniu open an account? Is it safe to open an account in qiniu
由文件图形丢失,说明自己都不用自己开发的OFFICE
Source of concurrent bugs (I) - visibility
Wei Lai: "pinches" the data and "pinches" the future
Mr developed by unity3d realizes model occlusion and transparent ground receiving shadow
Software project management 6.10 Cost budget
Tidb Primary course experience 8 (Management Maintenance of Clusters, add a tikv Node)
Ant financial services Yang Jun: evolution of ant data analysis platform and application of data analysis methods
Simple integration of client go gin six list watch two (about the improvement of RS, pod and deployment)
JS click the button to slide to the left
Leetcode 96. Different binary search trees
SparkStreaming实时数仓 问题&回答
CMakeLists.txt 如何编写
VDMA commissioning summary
Start with interpreting the code automatically generated by BDC, and explain the trial version of the program components of sapgui
[raise bar C #] how to call the base of the interface
[deep learning] the credit card fraud anomaly detection based on the deep learning autoencoder is very effective