当前位置:网站首页>图论(最近公共祖先LCA)
图论(最近公共祖先LCA)
2022-06-23 22:12:00 【Dαīsч】
一、基础
1、定义:在一棵有根树上,对于一个结点z,既是x的祖先,也是y的祖先,那么z是x,y的公共祖先,如果z在x,y的所有公共祖先中深度最大的,我们称之为最近公共祖先,记z = LCA(x,y)
2、暴力寻找(最坏时间复杂度O(n)):
(1)、从x向上走到根节点,并且标记经过的结点,然后令y向上走到根节点,当第一次遇到已标记的点时,就找到了LCA(x,y)
(2)、令x,y中较深的点先向上走到x,y等深处,然后同时向上访问,直到访问到同一结点,该结点就是LCA(x,y)
二、树上倍增法求LCA(在线)
倍增法求LCA=树上倍增法+暴力寻找第二种方法
1、树上倍增部分的dp表:
①设dp[x][k]表示x的2^k辈祖先,即向根节点走2^k步到达的结点
②如果这样的结点不存在则dp[x][k] = 0,那么dp[x][0]就代表x的父节点
③除此之外,对于k∈[1, log n],有dp[x][k] = dp[dp[x][k - 1]][k - 1],代表x的2^k辈祖先等同于x的2^(k - 1)辈祖先的2^(k - 1)辈祖先
我们可以对树进行遍历,一次计算每个点对应的dp数组中的值,顺便求出结点在树中的深度
2、利用dp数组求LCA
①令deep[x]>=deep[y],用二进制拆分思想,把x向上调整到与y同一深度。具体来说,就是x尝试向上走k=2^log n、……、2^1、2^0步,检查到达的结点是否比y深,则令x=dp[x][k],如果此时x = y,则LCA(x,y)=x
②利用二进制拆分思想,把x,y同时向上调整,保持同一深度,且二者不相会。具体来说,就是尝试向上走k = 2^log n、……、2^1、2^0步,如果dp[x][k] ≠ dp[y][k],则令x = dp[x][k],y = dp[y][k]此时x,y必定之差一步就相会了,他们的父节点dp[x][0]就是LCA(x,y)
3、代码实现
int to[maxn << 1], nex[maxn << 1], head[maxn];
int dp[maxn][32], deep[maxn], dis[maxn];
int cnt, nn, n, m, r;
void add(int u, int v)
{
to[++cnt] = v;
nex[cnt] = head[u];
head[u] = cnt;
}
void bfs(int root)
{
queue<int>q;
q.push(root);
deep[root] = 1;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = head[u]; i; i = nex[i])
{
int v = to[i];
if (deep[v])
continue;
deep[v] = deep[u] + 1;
dp[v][0] = u;
for (int j = 1; j <= nn; j++)
dp[v][j] = dp[dp[v][j - 1]][j - 1];
q.push(v);
}
}
}
void dfs(int x)
{
for (int i = 1; i <= nn; i++)
dp[x][i] = dp[dp[x][i - 1]][i - 1];
for (int i = head[x]; i; i = nex[i])
{
int y = to[i];
if (deep[y])
continue;
deep[y] = deep[x] + 1;
dp[y][0] = x;
dfs(y);
}
return;
}
int lca(int u, int v)
{
if (deep[u] > deep[v])
swap(u, v);
for (int i = nn; i >= 0; i--)
{
if (deep[dp[v][i]] >= deep[u])
v = dp[v][i];
}
if (u == v)
return u;
for (int i = nn; i >= 0; i--)
{
if (dp[u][i] != dp[v][i])
{
u = dp[u][i];
v = dp[v][i];
}
}
return dp[u][0];
}
void solve()
{
cin >> n >> m >> r;
nn = (int)(log(n) / log(2)) + 1;
for (int i = 1; i <= n; i++)
head[i] = deep[i] = 0;
cnt = 0;
for (int i = 0; i < n - 1; i++)
{
int u, v, w;
cin >> u >> v;
add(u, v);
add(v, u);
}
deep[r] = 1;
dfs(r);
//bfs(r);
for (int i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
cout << lca(u, v) << '\n';
}
}三、Tarjan求LCA(离线)
1、在深度优先遍历的任意时刻,一共有三种点:
①已经访问完毕并且回溯的结点,即子节点全部访问完毕,这些节点标记为2
②已经开始递归但是尚未回溯的结点,这些结点就是正在访问的结点x以及x的父节点,这些结点标记为1
③尚未访问的结点,标记为0
2、对于正在访问的结点x,它到根节点的路径已经标记为1,若此时y是已经访问并回溯的结点(表标记为2),则从y向上走到根,遇到的第一个标记为1的点就是LCA(x,y)
3、并查集优化:
当一个结点获得整数2的标记时,把它所在的集合合并到它的父节点所在的集合中,此时它的父节点一定标记为1,且单独构成一个集合。
这相当于每个完成回溯的结点都有一个指针指向它的父节点,只需查询y所在集合的代表元素,即find操作,就等价于从y向上一直走到一个开始递归但未完成回溯的结点,即LCA(x,y)
4、此时扫描与x相关的所有询问,若询问当中的一个点y的标记为2,那么LCA(x,y)就是find(y)
5、代码实现
int to[maxn << 1], nex[maxn << 1], head[maxn];
int fa[maxn], vis[maxn], ans[maxn];
vector<int>query[maxn], queryid[maxn];
int cnt, n, m, r;
void add(int u, int v)
{
to[++cnt] = v;
nex[cnt] = head[u];
head[u] = cnt;
}
void addquery(int u, int v, int id)
{
query[u].push_back(v);
query[v].push_back(u);
queryid[u].push_back(id);
queryid[v].push_back(id);
}
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void tarjan(int u)
{
vis[u] = 1;
for (int i = head[u]; i; i = nex[i])
{
int v = to[i];
if (vis[v])
continue;
tarjan(v);
fa[v] = u;
}
for (int i = 0; i < query[u].size(); i++)
{
int v = query[u][i], id = queryid[u][i];
if (vis[v] == 2)
ans[id] = find(v);
}
vis[u] = 2;
}
void solve()
{
cin >> n >> m >> r;
for (int i = 1; i <= n; i++)
{
fa[i] = i;
}
for (int i = 0; i < n - 1; i++)
{
int u, v;
cin >> u >> v;
add(u, v);
add(v, u);
}
for (int i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
if (u == v)
ans[i] = u;
else
addquery(u, v, i);
}
tarjan(r);
for (int i = 0; i < m; i++)
{
cout << ans[i] << '\n';
}
}边栏推荐
- 项目中常用到的 19 条 MySQL 优化
- Cs5213 HDMI to VGA with audio signal output scheme
- MySQL事務隔離
- Stm32 - - - - interruption externe
- PLC数据操作系列之构造不同应用场景的缓存栈FIFO(算法详解)
- 嵌入式接口之TIM定时器与NVIC的STM32模板库函数的一些解释
- 【Try to Hack】masscan
- 2022 cloud consulting technology series storage & CDN special sharing meeting
- Unknown character set index for field ‘255‘ received from server.
- 迪赛智慧数——柱状图(基本柱状图):2022年父亲节过节的方式
猜你喜欢

ORB_SLAM3环境搭建及demo演示

根据先序遍历和中序遍历生成后序遍历

【HackTheBox】Fawn
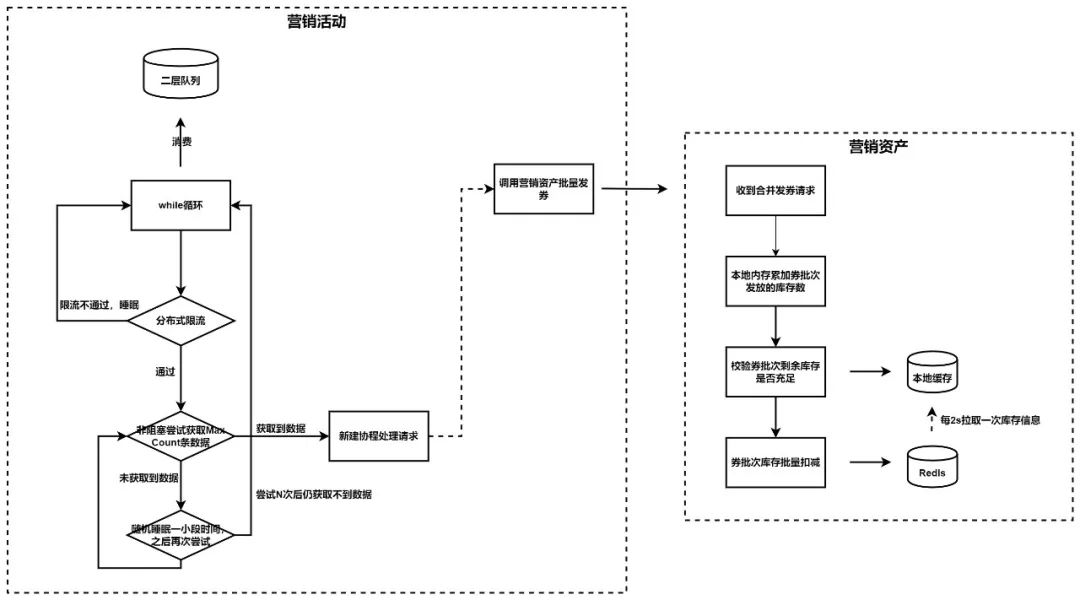
抖音支付十万级 TPS 流量发券实践
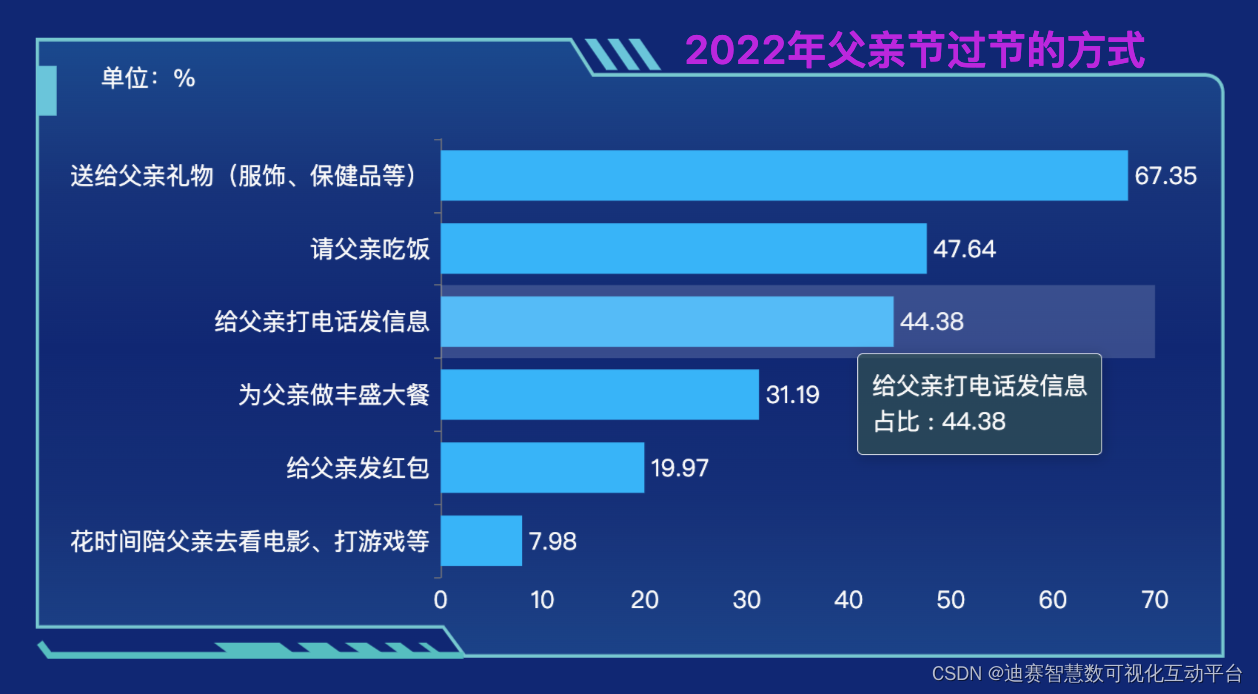
Desai wisdom number - histogram (basic histogram): the way to celebrate father's day in 2022

《阿里云天池大赛赛题解析》——O2O优惠卷预测

Ambire Guide: the arbitrum odyssey begins! Week 1 - Cross Chain Bridge
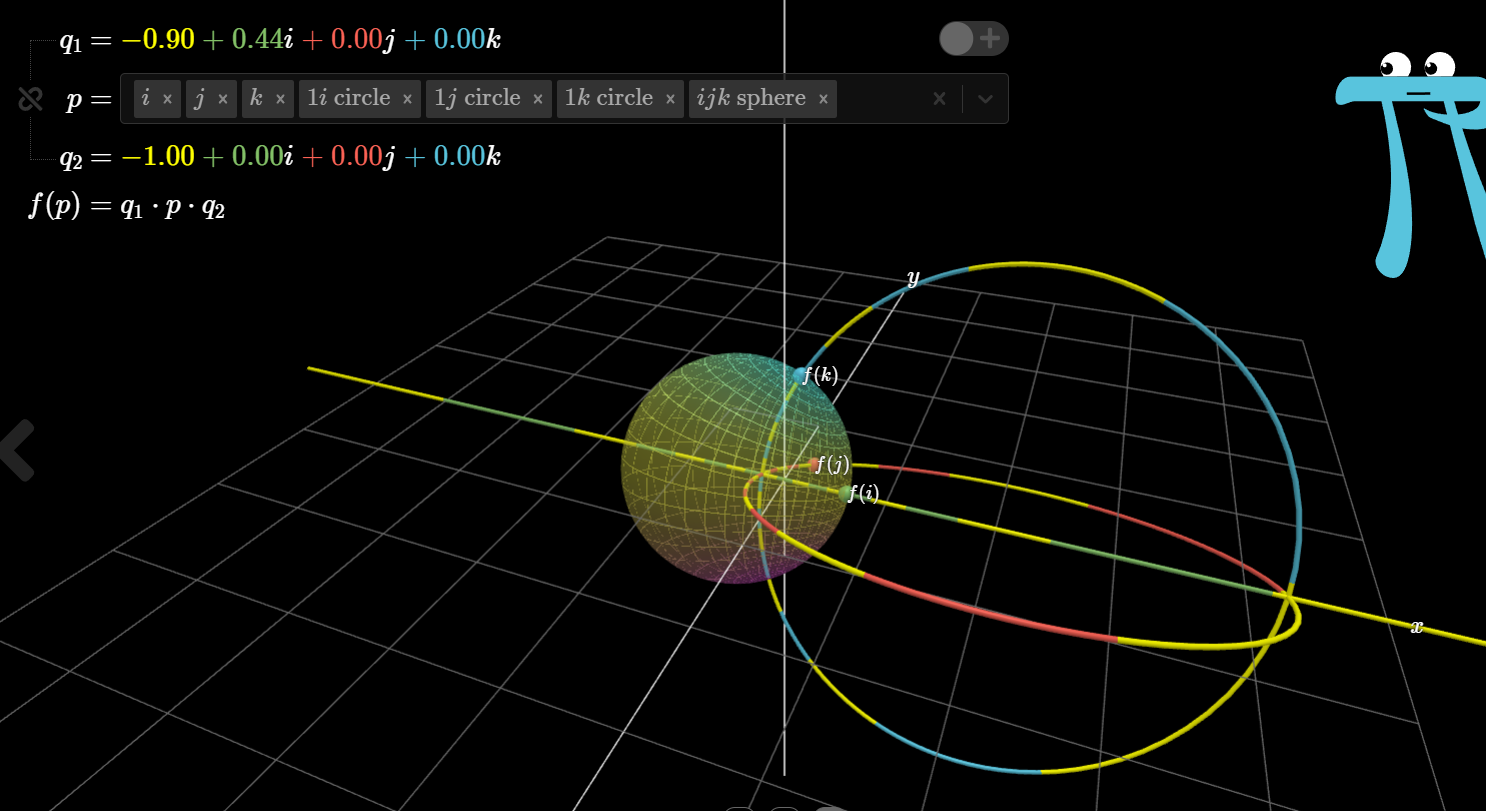
Detailed quaternion

Bilibili×蓝桥云课|线上编程实战赛全新上新!
云原生流水线工具汇总
随机推荐
Graph theory (tree diameter)
STM32-------定时器
百万消息量IM系统技术要点分享
Kotlin coroutine asynchronous flow
《阿里云天池大赛赛题解析》——O2O优惠卷预测
MySQL索引底层为什么用B+树?看完这篇文章,轻松应对面试。
【Xilinx AX7103 MicroBalze学习笔记6】MicroBlaze 自定义 IP 核封装实验
PHP的curl功能扩展基本用法
Autofac details
[design] 1359- how umi3 implements plug-in architecture
WebService client request failed can not create a secure xmlinputfactory
How to write and read ASM file system data
How does the fortress connection key server associate with the server host?
Avoid confusion when switching between arouter components
CTF go topic recurrence
How to handle the IP inconsistency in the contact when easygbs is cascaded with the upper level
STM32------ADC(电压检测)
【Try to Hack】masscan
迪赛智慧数——柱状图(基本柱状图):2022年父亲节过节的方式
Short video enters the hinterland of online music
