当前位置:网站首页>信息安全数学基础 Chapter 4——二次剩余与方根
信息安全数学基础 Chapter 4——二次剩余与方根
2022-06-11 17:13:00 【L3H_CoLin】
定义4.1 设m为正整数,若同余式 x 2 ≡ a ( m o d m ) , ( a , m ) = 1 x^2\equiv a(\mod m),(a,m)=1 x2≡a(modm),(a,m)=1,有解,则a称为模m的二次剩余,否则称为模m的二次非剩余
定义4.2 勒让德符号: ( a p ) (\frac{a}{p}) (pa),当a为模p的二次剩余时,值为1;非2次剩余时值为-1,若 p ∣ a p|a p∣a则值为0
定理4.1 p为素数,若 a ≡ b ( m o d p ) a\equiv b(\mod p) a≡b(modp),则 ( a p ) = ( b p ) (\frac{a}{p})=(\frac{b}{p}) (pa)=(pb)
求同余式 x 2 ≡ a ( m o d p ) x^2\equiv a(\mod p) x2≡a(modp)的解可以看成是在有限域 Z p \mathbb Z_p Zp中求多项式 x 2 − a x^2-a x2−a的根。
定理4.2 欧拉判别法则:p为奇素数,则对于任意整数a, ( a p ) ≡ a p − 1 2 ( m o d p ) (\frac{a}{p})\equiv a^{\frac{p-1}{2}}(\mod p) (pa)≡a2p−1(modp)
证明:
设 g g g是 Z p \mathbb Z_p Zp的本原元,则 Z p ∗ = { g 0 , g 1 , . . . , g p − 2 } \mathbb Z_p^*=\{g^0,g^1,...,g^{p-2}\} Zp∗={ g0,g1,...,gp−2}
对于所有 0 ≤ i ≤ p − 1 2 0\le i\le \frac{p-1}{2} 0≤i≤2p−1, ( g 2 i ) p − 1 2 = ( g p − 1 ) i = 1 , ( g 2 i + 1 ) p − 1 2 = ( g p − 1 ) i g p − 1 2 , g p − 1 2 = − 1 (g^{2i})^{\frac{p-1}{2}}=(g^{p-1})^i=1,(g^{2i+1})^{\frac{p-1}{2}}=(g^{p-1})^ig^{\frac{p-1}{2}},g^{\frac{p-1}{2}}=-1 (g2i)2p−1=(gp−1)i=1,(g2i+1)2p−1=(gp−1)ig2p−1,g2p−1=−1(由g为本原元可知 g p − 1 2 ≠ 1 g^{\frac{p-1}{2}}\ne 1 g2p−1=1,但 ( g p − 1 2 ) 2 = 1 (g^{\frac{p-1}{2}})^2= 1 (g2p−1)2=1,故其只能为-1),故 ( g p − 1 2 ) 2 i + 1 = − 1 (g^{\frac{p-1}{2}})^{2i+1}=-1 (g2p−1)2i+1=−1
由于考虑模p的二次同余式,因此a可以看做是 Z p \mathbb Z_p Zp中与之同余等价的元素
当 a ≡ g 2 i ( m o d p ) , 0 ≤ i < p − 1 2 a\equiv g^{2i}(\mod p),0\le i<\frac{p-1}{2} a≡g2i(modp),0≤i<2p−1,多项式 x 2 − a = x 2 − g 2 i x^2-a=x^2-g^{2i} x2−a=x2−g2i有根±gi,故 ( a p ) = 1 ≡ a p − 1 2 ( m o d p ) (\frac{a}{p})=1\equiv a^{\frac{p-1}{2}}(\mod p) (pa)=1≡a2p−1(modp)
当 a ≡ g 2 i + 1 ( m o d p ) , 0 ≤ i < p − 1 2 a\equiv g^{2i+1}(\mod p),0\le i<\frac{p-1}{2} a≡g2i+1(modp),0≤i<2p−1,多项式 x 2 − a = x 2 − g 2 i + 1 x^2-a=x^2-g^{2i+1} x2−a=x2−g2i+1一定没有根。否则若 x 0 2 = g 2 i + 1 x_0^2=g^{2i+1} x02=g2i+1,那么 1 = ( x 0 2 ) p − 1 2 = ( g 2 i + 1 ) p − 1 2 = − 1 1=(x_0^2)^{\frac{p-1}{2}}=(g^{2i+1})^{\frac{p-1}{2}}=-1 1=(x02)2p−1=(g2i+1)2p−1=−1矛盾。故 ( a p ) = − 1 ≡ a p − 1 2 ( m o d p ) (\frac{a}{p})=-1\equiv a^{\frac{p-1}{2}}(\mod p) (pa)=−1≡a2p−1(modp)
由上述定理可知,模p的二次剩余有 p − 1 2 \frac{p-1}{2} 2p−1个(本原元的所有偶数次幂)
推论 设p为奇素数,则
( 1 p ) = 1 (\frac{1}{p})=1 (p1)=1
( − 1 p ) = ( − 1 ) p − 1 2 (\frac{-1}{p})=(-1)^\frac{p-1}{2} (p−1)=(−1)2p−1
( a b p ) = ( a p ) ( b p ) (\frac{ab}{p})=(\frac{a}{p})(\frac{b}{p}) (pab)=(pa)(pb)
( a n p ) = ( a p ) n , n > 0 (\frac{a^n}{p})=(\frac{a}{p})^n,n>0 (pan)=(pa)n,n>0
定理4.3 设p为奇素数,则 ( 2 p ) = ( − 1 ) p 2 − 1 8 (\frac{2}{p})=(-1)^{\frac{p^2-1}{8}} (p2)=(−1)8p2−1
证明:构造证明
( p − 1 ) ! ≡ 1 ⋅ 3 ⋅ 5 ⋅ . . . ⋅ ( p − 2 ) ⋅ 2 ⋅ 4 ⋅ . . . ⋅ ( p − 1 ) (p-1)!\equiv 1\cdot 3\cdot 5\cdot ... \cdot (p-2)\cdot 2\cdot 4\cdot ... \cdot (p-1) (p−1)!≡1⋅3⋅5⋅...⋅(p−2)⋅2⋅4⋅...⋅(p−1)
对于4k+1型的p有
≡ 1 ⋅ ( p − 2 ) ⋅ 3 ⋅ ( p − 4 ) ⋅ 5 ⋅ . . . ⋅ p − 3 2 ⋅ ( p − p − 1 2 ) ⋅ 2 p − 1 2 ⋅ ( p − 1 2 ! ) ( m o d p ) \equiv 1\cdot (p-2)\cdot 3\cdot (p-4)\cdot 5\cdot ...\cdot \frac{p-3}{2}\cdot (p-\frac{p-1}{2})\cdot 2^{\frac{p-1}{2}}\cdot (\frac{p-1}{2}!)(\mod p) ≡1⋅(p−2)⋅3⋅(p−4)⋅5⋅...⋅2p−3⋅(p−2p−1)⋅22p−1⋅(2p−1!)(modp)(后面一半所有偶数提个2出来,前半部分可以交替提一个-1)
≡ ( − 1 ) p − 1 4 ⋅ 2 p − 1 2 ⋅ ( p − 1 2 ! ) 2 ( m o d p ) \equiv (-1)^{\frac{p-1}{4}}\cdot 2^{\frac{p-1}{2}}\cdot(\frac{p-1}{2}!)^2(\mod p) ≡(−1)4p−1⋅22p−1⋅(2p−1!)2(modp)
对于4k+3型的p有
≡ 1 ⋅ ( p − 2 ) ⋅ 3 ⋅ ( p − 4 ) ⋅ 5 ⋅ . . . ⋅ ( p − p − 3 2 ) ⋅ p − 1 2 ⋅ 2 p − 1 2 ⋅ ( p − 1 2 ! ) ( m o d p ) \equiv 1\cdot (p-2)\cdot 3\cdot (p-4)\cdot 5\cdot ...\cdot(p-\frac{p-3}{2})\cdot\frac{p-1}{2}\cdot 2^{\frac{p-1}{2}}\cdot (\frac{p-1}{2}!)(\mod p) ≡1⋅(p−2)⋅3⋅(p−4)⋅5⋅...⋅(p−2p−3)⋅2p−1⋅22p−1⋅(2p−1!)(modp)
≡ ( − 1 ) p − 3 4 ⋅ 2 p − 1 2 ⋅ ( p − 1 2 ! ) 2 ( m o d p ) \equiv (-1)^{\frac{p-3}{4}}\cdot 2^{\frac{p-1}{2}}\cdot(\frac{p-1}{2}!)^2(\mod p) ≡(−1)4p−3⋅22p−1⋅(2p−1!)2(modp)
Wilson定理知 ( p − 1 ) ! ≡ − 1 ( m o d p ) (p-1)!\equiv -1(\mod p) (p−1)!≡−1(modp),及 ( p − 1 2 ! ) 2 ≡ ( − 1 ) p + 1 2 ( m o d p ) (\frac{p-1}{2}!)^2\equiv(-1)^{\frac{p+1}{2}}(\mod p) (2p−1!)2≡(−1)2p+1(modp)(转化为 ( − 1 ) p − 1 2 ( p − 1 ) ! (-1)^{\frac{p-1}{2}}(p-1)! (−1)2p−1(p−1)!) 可知当 p ≡ ± 1 ( m o d 8 ) p\equiv ±1(\mod 8) p≡±1(mod8)时, 2 p − 1 2 ≡ 1 ( m o d p ) 2^{\frac{p-1}{2}}\equiv 1(\mod p) 22p−1≡1(modp),当 p ≡ ± 3 ( m o d 8 ) p\equiv ±3(\mod 8) p≡±3(mod8)时, 2 p − 1 2 ≡ − 1 ( m o d p ) 2^{\frac{p-1}{2}}\equiv -1(\mod p) 22p−1≡−1(modp),综合验证得 2 p − 1 2 ≡ ( − 1 ) p 2 − 1 8 ( m o d p ) 2^{\frac{p-1}{2}}\equiv(-1)^{\frac{p^2-1}{8}}(\mod p) 22p−1≡(−1)8p2−1(modp),由欧拉判别法则 ( 2 p ) = ( − 1 ) p 2 − 1 8 (\frac{2}{p})=(-1)^{\frac{p^2-1}{8}} (p2)=(−1)8p2−1
定理4.4 二次互反律:p,q是互素奇素数,则 ( q p ) = ( − 1 ) p − 1 2 q − 1 2 ( p q ) (\frac{q}{p})=(-1)^{\frac{p-1}{2}\frac{q-1}{2}}(\frac{p}{q}) (pq)=(−1)2p−12q−1(qp)
证明:太复杂了,不要求掌握
定义4.3 雅可比符号: m = ∏ i = 1 n p i , p i m=\prod_{i=1}^np_i,p_i m=∏i=1npi,pi是奇素数,对于任意整数a定义a模m的雅可比符号为 ( a m ) = ∏ i = 1 n ( a p i ) (\frac{a}{m})=\prod_{i=1}^n(\frac{a}{p_i}) (ma)=∏i=1n(pia),m为奇素数时,其雅克比符号就是勒让德符号。
定理4.5 设m为正奇数, a ≡ b ( m o d m ) ⇒ ( a m ) = ( b m ) a\equiv b(\mod m)\Rightarrow (\frac{a}{m})=(\frac{b}{m}) a≡b(modm)⇒(ma)=(mb)
定理4.6 设m为正奇数,则
(1) ( 1 m ) = 1 (\frac{1}{m})=1 (m1)=1
(2) ( a b m ) = ( a m ) ( b m ) (\frac{ab}{ m})=(\frac{a}{m})(\frac{b}{m}) (mab)=(ma)(mb)
(3) ( a n m ) = ( a m ) n (\frac{a^n}{m})=(\frac{a}{m})^n (man)=(ma)n
(4) ( − 1 m ) = ( − 1 ) m − 1 2 (\frac{-1}{m})=(-1)^{\frac{m-1}{2}} (m−1)=(−1)2m−1
(5) ( 2 m ) = ( − 1 ) m 2 − 1 8 (\frac{2}{m})=(-1)^{\frac{m^2-1}{8}} (m2)=(−1)8m2−1
定理4.7 设m,n为正奇数,则 ( n m ) = ( − 1 ) m − 1 2 n − 1 2 ( m n ) (\frac{n}{m})=(-1)^{\frac{m-1}{2}\frac{n-1}{2}}(\frac{m}{n}) (mn)=(−1)2m−12n−1(nm)
定义4.4 二次剩余问题:未知n的分解式的情况下,一般性地判断一个整数a是否是模n的二次剩余是一个难解的问题,称为二次剩余问题。
加密算法1——Rabin加密算法
Alice选择两个4k+3型的素数(称为Blum素数)p,q,计算n=pq,将p,q作为私钥公开n。
加密:明文为整数m,密文c=m2(mod n)
解密:解同余方程c=x2(mod n)可以得到4个解,选择其中有意义的解作为明文m。
计算方法——a=x2(mod p),p=4k+3的解法
若上式有解,则在[0,p-1]中一定有解,因此数字不大时可以对a一直加p直到找到一个完全平方数即可(这种方法对p无4k+3的限制,但是p很大时不方便)
由 ( a p ) = 1 (\frac{a}{p})=1 (pa)=1由欧拉判别法则 a p − 1 2 ≡ 1 ( m o d p ) a^{\frac{p-1}{2}}\equiv 1(\mod p) a2p−1≡1(modp),故有 ( a p − 1 4 ) 2 ≡ a ( m o d p ) (a^{\frac{p-1}{4}})^2\equiv a(\mod p) (a4p−1)2≡a(modp),故解为 x ≡ ± a p − 1 4 ( m o d p ) x\equiv ±a^{\frac{p-1}{4}}(\mod p) x≡±a4p−1(modp)
加密算法2——Goldwasser-Micali加密算法
Alice选择两个不同的素数p,q,和整数y满足 ( y p ) = ( y q ) = − 1 (\frac{y}{p})=(\frac{y}{q})=-1 (py)=(qy)=−1。计算n=pq,p和q座位私钥公开n,y
加密:将二进制整数m作为明文,第i位记为bi,对于每一位,随机选择0<xi<n,若该位为0计算ci=xi2(mod n),否则计算ci=yxi2(mod n),密文为所有的c
解密:若ci为模n的二次剩余,则判断bi=0,否则bi=1
定义4.5 设<g>是一个由元素g生成的一个n元循环群,则对于任意a∈<g>,存在0≤i<n,a=gi,称i为以g为底a的指标,记作indga。求指标的问题,在密码学中通常称为离散对数问题。n充分大的整数时求解离散对数问题为一个难解问题。
定理4.8 设<g>是一个n元循环群,a∈<g>,如果对于正整数m有:
(1) am=e
(2) 对于任意素因子p|m, a m p ≠ e a^{\frac{m}{p}}\ne e apm=e,则ord(a)=m,且m|n
定义4.8 原根:设m为正整数,整数a满足(a,m)=1,a模m的阶ordm(a)是指a(mod m)在 Z m ∗ \mathbb Z_m^* Zm∗中的阶;如果 Z m ∗ \mathbb Z_m^* Zm∗为循环群,整数a称为模m的原根是指a(mod m)为 Z m ∗ \mathbb Z_m^* Zm∗的生成元
根据上述定义,a所在模m剩余类中所有整数的模m阶均为ordm(a)
根据原根定义:当m=2,4时,模m原根分别为1,3
一般地,当且仅当m=2,4,pa,2pa(p为奇素数,a≥1),模m有原根
定理4.9 设<g>是一个n元循环群,a,b∈<g>,则indgab ≡ \equiv ≡indga+indgb(mod n)
证明:indga=x,indgb=y,则gx+y=ab= g i n d g a b g^{ind_gab} gindgab
即 g x + y − i n d g a b = e g^{x+y-ind_gab}=e gx+y−indgab=e,又ord(g)=n,故n|x+y-indgab,故结论成立
定义4.9 设m是大于1的正整数,如果n次同余式xn=a(mod m), (a,m)=1有解,则a称作模m的n次剩余,否则为模m的n次非剩余。
定理4.14 (高次剩余)设m为大于1的正整数,g为模m的一个原根,(a,m)=1,d=(n, φ \varphi φ(m)),那么xn=a(mod m)有解的充要条件为 a φ ( m ) d ≡ 1 ( m o d m ) a^{\frac{\varphi(m)}{d}}\equiv 1(\mod m) adφ(m)≡1(modm)
证明:g为模m的一个原根,所以 Z m ∗ = < g > , x n ≡ a ( m o d m ) \mathbb Z_m^*=<g>,x^n\equiv a(\mod m) Zm∗=<g>,xn≡a(modm)有解的充要条件是 i n d g x n = i n d g a ⇒ n i n d g x ≡ i n d g a ( m o d φ ( m ) ) ind_gx^n=ind_ga\Rightarrow nind_gx\equiv ind_ga(\mod \varphi(m)) indgxn=indga⇒nindgx≡indga(modφ(m))(注意模m的循环群一共只有 φ ( m ) \varphi(m) φ(m)个元素,因此要模 φ ( m ) \varphi(m) φ(m)!),令X=indgx,则有 n X ≡ i n d g a ( m o d φ ( m ) ) nX\equiv ind_ga(\mod \varphi(m)) nX≡indga(modφ(m))
该一次同余式有解的充要条件为(n,φ(m))|indga,即d|indga,等价于indga ≡ \equiv ≡ 0(mod d)
由定理2.4(4)有 φ ( m ) d i n d g a ≡ 0 ( m o d φ ( m ) ) \frac{\varphi(m)}{d}ind_ga\equiv 0(\mod \varphi(m)) dφ(m)indga≡0(modφ(m))。两边取“指数”得 a φ ( m ) d ≡ 1 ( m o d m ) a^{\frac{\varphi(m)}{d}}\equiv 1(\mod m) adφ(m)≡1(modm),故原命题成立。
注:该定理还能帮助求解高次同余式的解数。对于同余式 a x ≡ b ( m o d m ) ax\equiv b(\mod m) ax≡b(modm),其有解的充要条件为 ( a , m ) ∣ b (a,m)|b (a,m)∣b,且通解可以写成 x = x 0 + m ( a , m ) t , t = 0 , 1 , . . . , ( a , m ) − 1 x=x_0+\frac{m}{(a,m)}t,t=0,1,...,(a,m)-1 x=x0+(a,m)mt,t=0,1,...,(a,m)−1的形式,因此解的数量为 ( a , m ) (a,m) (a,m)。那么 n X ≡ i n d g a ( m o d φ ( m ) ) nX\equiv ind_ga(\mod \varphi(m)) nX≡indga(modφ(m))的解数应该有 ( n , φ ( m ) ) (n,\varphi(m)) (n,φ(m))个
边栏推荐
- Database backup (MySQL)
- Authing Share|理解 SAML2 协议
- SQL injection attack under seed emulator (including SQL environment configuration)
- LeetCode-1005. K 次取反后最大化的数组和
- C language: use H and C. summary of problems encountered in documents
- Oracle generates non duplicate string sys_ Guid() and MySQL generate unique values
- Tornado environment construction and basic framework construction -- familiar Hello World
- 定制 or 订阅?未来中国 SaaS 行业发展趋势是什么?
- Exception handling and exception usage in golang
- 搜狐全員遭詐騙,暴露哪些問題?
猜你喜欢

Environment configuration and pymysql installation
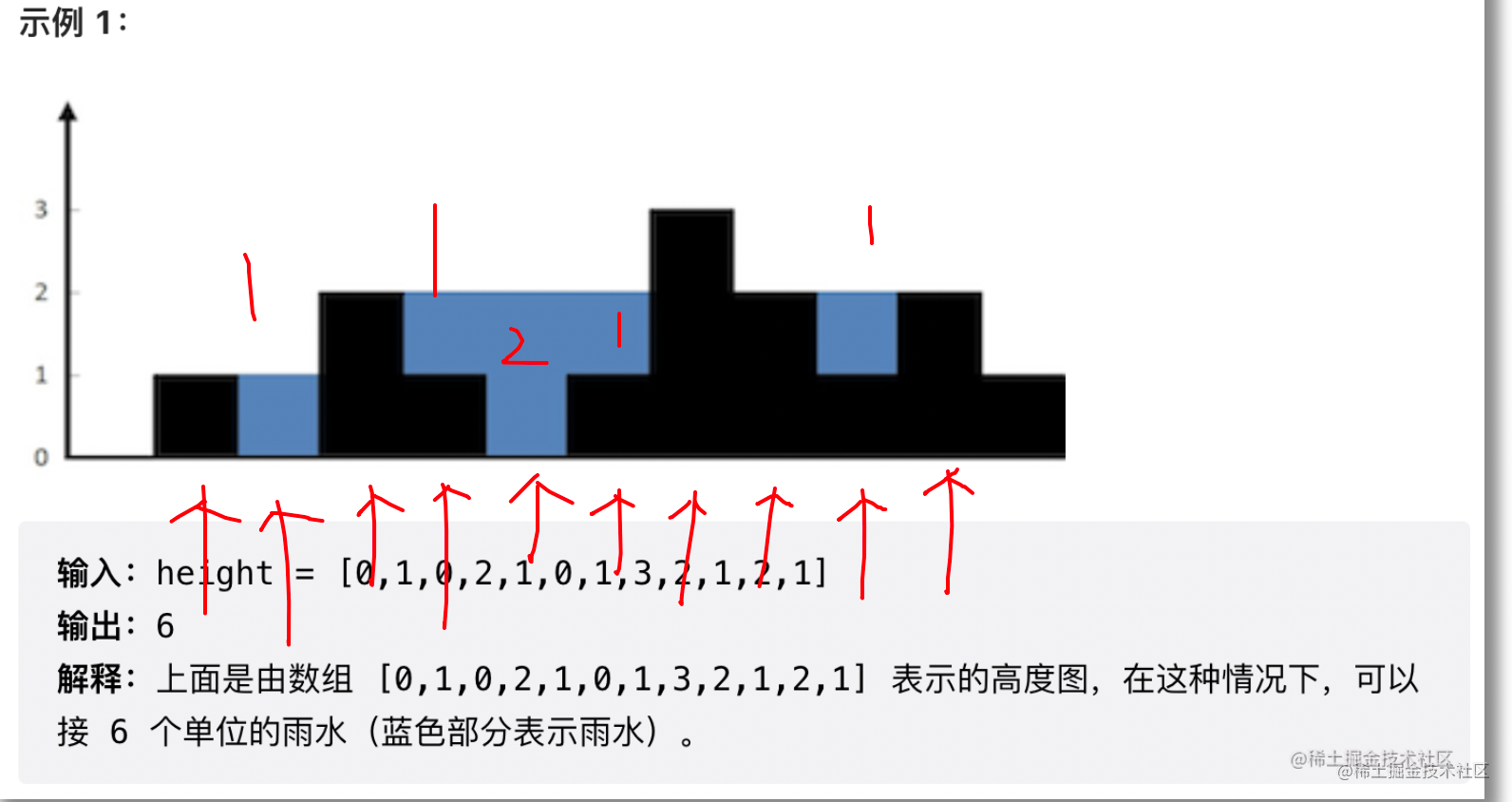
LeetCode——42. Connected to rainwater (double pointer)

Analysis report on future development trend and investment suggestions of global and Chinese soybean protein industry 2022-2028

搜狐全員遭詐騙,暴露哪些問題?

vscode保存代碼時自動eslint格式化
Authing CEO 谢扬入选福布斯 2021 年 30 Under 30 亚洲榜单

Axi protocol Basics

论文阅读 dyngraph2vec: Capturing Network Dynamics using Dynamic Graph Representation Learning

A set of ThinkPHP wechat applet mall source code with background management

JINTE NET基金会将通过线上直播参与维度链全球战略发布会
随机推荐
Global and Chinese molten carbonate fuel cell industry outlook and market panoramic Research Report 2022-2028
seed-emulator下进行sql注入攻击(含sql环境配置)
Global and China Mobile Network Optimization (MnO) industry development panoramic survey and Investment Strategy Research Report 2022-2028
Is the second-class cost engineer worth the exam? What is the development prospect?
Analysis report on the "fourteenth five year plan" proposal and innovation environment of global and Chinese sodium pyrophosphate industry (2022-2028)
Recyclerview cache reuse analysis, source code interpretation
LeetCode——24. Exchange the nodes in the linked list in pairs (three pointers)
Katalon Studio Enterprise
Difference between select into from and insert into select
用实际案例分析PMP与ACP应该考哪个?哪个更有用?
Haas, which integrates relevant technologies of Alibaba cloud, Dharma Institute and pingtouge, has officially announced the book
我的CのERROR们
^31原型面试题
Research Report on operation mode and investment opportunities of China's aluminum industry 2022-2028
Docker安装mysql5.7(开启binlog功能、修改字符)
04_特征工程—特征选择
ASP.NET教育OA系统源码 教育行业OA系统源码带文档
Database backup (MySQL)
^31 prototype interview questions
The use of histogram function in MATLAB