当前位置:网站首页>Principle of finding combinatorial number and template code
Principle of finding combinatorial number and template code
2022-07-02 01:06:00 【Alkali!】
Type 1 : Put C Array preprocessing ( Recurrence )
Background

Ideas



According to the combination number recurrence formula , First The number of combinations to be used in the range is pre processed and tabulated
C a b = C a − 1 b + C a − 1 b − 1 C_{a}^{b}=C_{a-1}^{b}+C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1
prove :
stay a Take from one ball b A ball , How many ways are there ?
Yes C a b C_{a}^{b} Cab Kind of
You can think of a ball c Very special , Then take b There are two ways to get a ball : Fetch c Still don't get it c
Fetch c: C a − 1 b − 1 C_{a-1}^{b-1} Ca−1b−1( In addition a-1 Take from one ball b-1 individual )
Can't get c: C a − 1 b C_{a-1}^{b} Ca−1b( stay a-1 Take... From a ball b individual )
// Background :AcWing 885
#include<iostream>
using namespace std;
const int N=2010,mod=1e9+7;
int c[N][N];
void init()
{
for(int i=0;i<N;i++) //N Is the upper limit of the subscript of the combinatorial number
for(int j=0;j<=i;j++)
if(!j) c[i][j]=1; // If the superscript is 0, That means not taking any , There is only one case , Note that this is not 0, It is 1
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; // Take the mold when calculating
}
Template code
// Background :AcWing 885
#include<iostream>
using namespace std;
const int N=2010,mod=1e9+7;
int c[N][N];
void init()
{
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(!j) c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
int main()
{
init();
int n,a,b;
scanf("%d",&n);
while(n--)
{
scanf("%d%d",&a,&b);
printf("%d\n",c[a][b]);
}
return 0;
}
Type 2 : Preprocessing out factorials
Background

Ideas


- Why does this problem require an inverse element , Can't you just divide by the corresponding factorial ?


Template code
// Background AcWing 886
#include<iostream>
using namespace std;
const int N=100010,mod=1e9+7;
typedef long long LL;
int fact[N],infact[N];
int n,a,b;
int qmi(int a,int b,int p) // Fast power algorithm
{
int res=1;
while(b)
{
if(b&1) res=(LL)res*a%p;
a=(LL)a*a%p;
b=b>>1;
}
return res;
}
int main()
{
fact[0]=1,infact[0]=1;
for(int i=1;i<N;i++) // Preprocess factorials and inverse elements of factorials
{
fact[i]=(LL)fact[i-1]*i%mod;
infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;
}
scanf("%d",&n);
while(n--)
{
scanf("%d%d",&a,&b);
printf("%d\n",(LL)fact[a]*infact[b]%mod*infact[a-b]%mod);
}
return 0;
}
(LL) On the left are int value , Explain to confirm The end result is a int Values in range , Because in the end, it's all molded mod Yes ! But in the specific calculation process, multiplication first may explode int, If you use int Saving may lead to data errors , So here (LL) The function of should be Temporarily store the data in LL Within the range of , To ensure correctness , Finally get another int Result .
Type 3 : Use Lucas theorem to recursively narrow the scope
Background

The upper and lower limits of the combination number are particularly large
Ideas

utilize lucas Theorem to simplify calculation
lucas Theorem content :
Use Lucas theorem to recurse downward , hold a、b Reduce to scale p Small number , Then calculate the factorial directly .
Time complexity :
Template code
// Background :AcWing 887
#include<iostream>
using namespace std;
typedef long long LL;
int n,p;
LL a,b;
int qmi(int a,int b,int p) // Fast power algorithm
{
int res=1;
while(b)
{
if(b&1) res=(LL)res*a%p;
a=(LL)a*a%p;
b=b>>1;
}
return res;
}
int C(int a,int b,int p) // Directly calculate the number of combinations
{
if(b>a) return 0;
int res=1;
for(int i=1,j=a;i<=b;i++,j--)
{
res=(LL)res*j%p;
res=(LL)res*qmi(i,p-2,p)%p;
}
return res;
}
int lucas(LL a,LL b,int p) // Lucas theorem
{
if(a<p&&b<p) return C(a,b,p);
else return (LL)C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main()
{
scanf("%d",&n);
while(n--)
{
scanf("%lld%lld%d",&a,&b,&p);
printf("%d\n",lucas(a,b,p));
}
return 0;
}
Type four : Calculate the number accurately , No more mold taking ( High precision multiplication )
Background

Ideas
First, we decompose the prime factor , Then use high-precision multiplication to calculate this combined number .
Specific steps :
- 1. hold 1 − a 1-a 1−a Sift out all primes between ( Linear sieve method )
void get_primes(int n)
{
for(int i=2;i<=n;i++)
{
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]*i<=n;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0)break;//==0 Every leak
}
}
}
- To calculate the C a b C_{a}^{b} Cab in 1 − a 1-a 1−a How many primes do they contain
principle :
int get(int n,int p)
{
int res =0;
while(n)
{
res+=n/p;
n/=p;
}
return res;
}
// In the main function
for(int i=0;i<cnt;i++)
{
int p = primes[i];
sum[i] = get(a,p)-get(a-b,p)-get(b,p);
}
- Multiply all prime factors with high precision
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
// In the main function
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )//primes[i] The number of times
res = mul(res, primes[i]);
- Output the answer
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
Template code
#include<iostream>
#include<vector>
using namespace std;
int a,b;
const int N=5010;
int primes[N],cnt,sum[N];
bool st[N];
void get_primes(int n) // Linear sieve method
{
for(int i=2;i<=n;i++)
{
if(!st[i]) primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;
if(i%primes[j]==0) break;
}
}
}
int get(int n,int p) // Calculate the number of times the prime number appears
{
int res=0;
while(n)
{
res+=n/p;
n/=p;
}
return res;
}
vector<int> mul(vector<int> a,int b) // High precision multiplication
{
// here b Definitely not for 0
vector<int> c;
int t=0;
for(int i=0;i<a.size()||t;i++)
{
if(i<a.size()) t+=a[i]*b;
c.push_back(t%10);
t/=10;
}
return c;
}
int main()
{
scanf("%d%d",&a,&b);
get_primes(a); // Sieve prime number
for(int i=0;i<cnt;i++) // Calculate the number of prime occurrences
{
int p=primes[i];
sum[i]=get(a,p)-get(b,p)-get(a-b,p);
}
vector<int> res;
res.push_back(1); // The initial value of the assignment is 1
// Decomposing prime factor , The prime factor is obtained , We also get the number of times of each prime factor , At this time, multiply them repeatedly , Use high-precision multiplication to calculate
for(int i=0;i<cnt;i++)
for(int j=0;j<sum[i];j++)
res=mul(res,primes[i]);
for(int i=res.size()-1;i>=0;i--) printf("%d",res[i]);
return 0;
}
边栏推荐
- [leetcode] number of maximum consecutive ones
- Leetcode skimming: stack and queue 05 (inverse Polish expression evaluation)
- Global and Chinese markets for maritime services 2022-2028: Research Report on technology, participants, trends, market size and share
- 工作中非常重要的测试策略,你大概没注意过吧
- Han Zhichao: real time risk control practice of eBay based on graph neural network
- 2022 low voltage electrician examination questions and answers
- 测试人进阶技能:单元测试报告应用指南
- Schrodinger's Japanese learning applet source code
- [JS download files through url]
- Entrepreneurship is a little risky. Read the data and do a business analysis
猜你喜欢
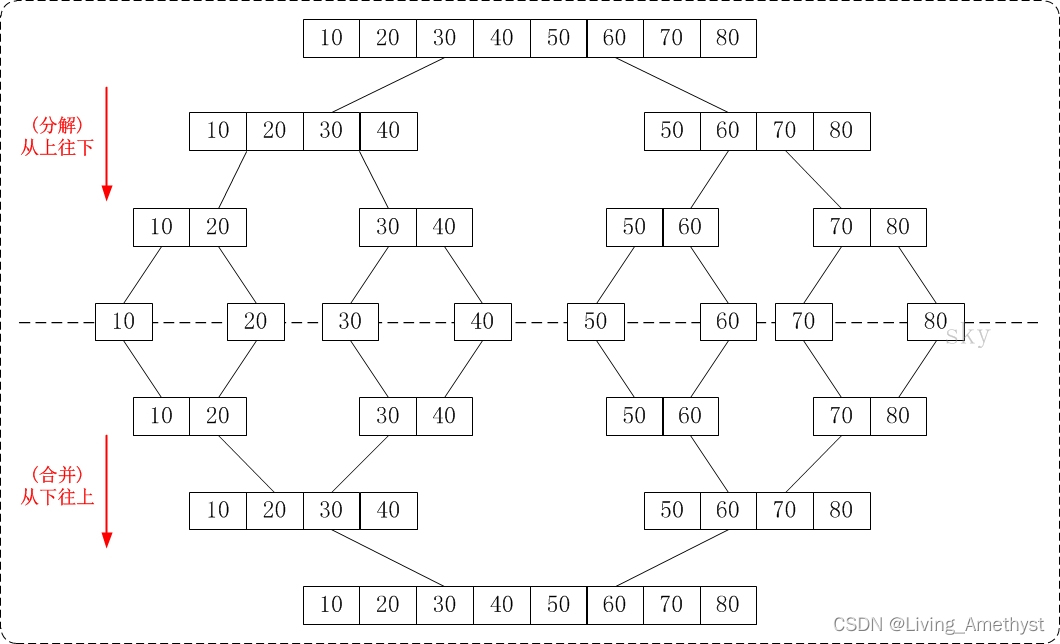
【八大排序④】归并排序、不基于比较的排序(计数排序、基数排序、桶排序)

sso单点登录的实现。

Output results of convolution operation with multiple tensors and multiple convolution kernels
![[leetcode] number of maximum consecutive ones](/img/70/7f3d1c8e0ab2698d98220cca911209.png)
[leetcode] number of maximum consecutive ones

Datawhale 社区黑板报(第1期)
Leetcode skimming: stack and queue 02 (realizing stack with queue)
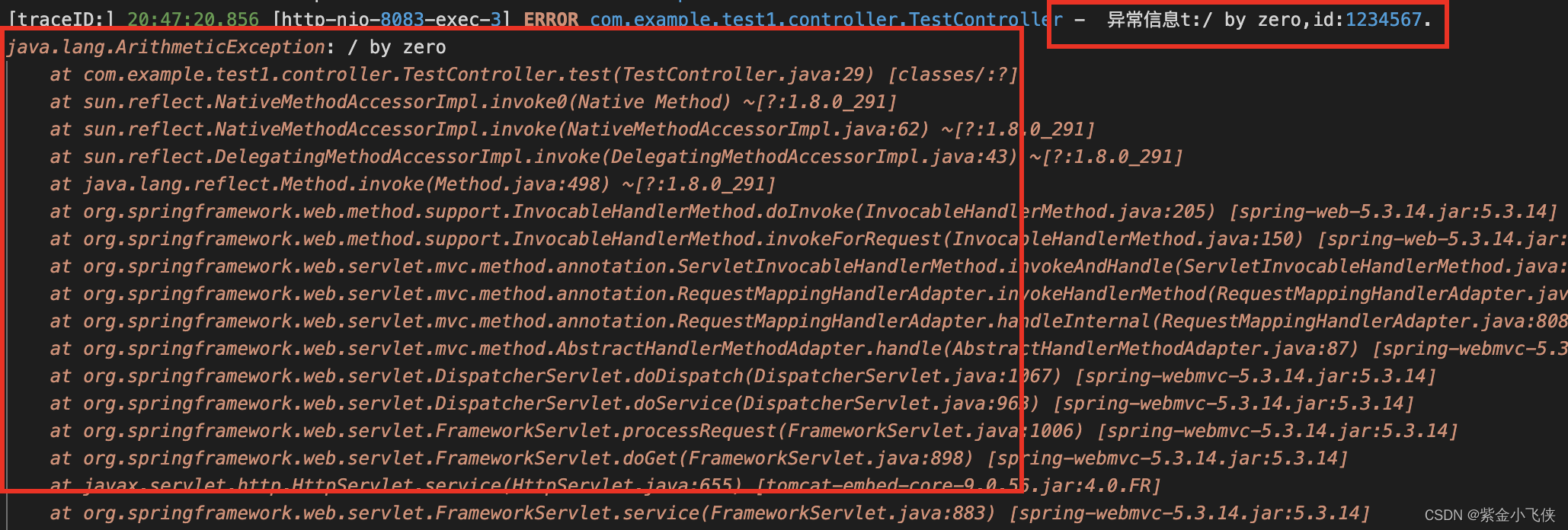
Slf4j print abnormal stack information
Leetcode skimming: stack and queue 03 (valid parentheses)
Promise和模块块化编程

excel查找与引用函数
随机推荐
From 20s to 500ms, I used these three methods
工作中非常重要的测试策略,你大概没注意过吧
[WesternCTF2018]shrine writeup
[bottom pop-up selector] uniapp picker component - scroll selector popped up at the bottom
Slf4j print abnormal stack information
Friends circle community program source code sharing
Node -- add compressed file
Picture puzzle wechat applet source code_ Support multi template production and traffic master
2022 pinduoduo details / pinduoduo product details / pinduoduo SKU details
[JS download files through url]
UDS bootloader of s32kxxx bootloader
[leetcode] number of maximum consecutive ones
Global and Chinese markets for maritime services 2022-2028: Research Report on technology, participants, trends, market size and share
Leetcode skimming: stack and queue 06 (top k high-frequency elements)
Global and Chinese market of aircraft MRO software 2022-2028: Research Report on technology, participants, trends, market size and share
Otaku wallpaper Daquan wechat applet source code - with dynamic wallpaper to support a variety of traffic owners
AIX存储管理之逻辑卷的创建及属性的查看和修改
Bilstm CRF code implementation
What are the differences between software testers with a monthly salary of 7K and 25K? Leaders look up to you when they master it
RFID makes the inventory of fixed assets faster and more accurate