当前位置:网站首页>leetcode518,377
leetcode518,377
2022-07-05 00:23:00 【The left wheel of fate】
List of articles
518. Change for II
Give you an array of integers coins Coins of different denominations , Give another integer amount Represents the total amount .
Please calculate and return the number of coin combinations that can be rounded up to the total amount . If no combination of coins can make up the total amount , return 0 .
Suppose that there are infinite coins of each denomination .
The subject data ensure that the results meet 32 Bit signed integer .
Example 1:
Input :amount = 5, coins = [1, 2, 5]
Output :4
explain : There are four ways to make up the total amount :
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
Example 2:
Input :amount = 3, coins = [2]
Output :0
explain : Use only face value 2 We can't make up the total amount of 3 .
Example 3:
Input :amount = 10, coins = [10]
Output :1
Tips :
1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins All the values in Different from each other
0 <= amount <= 5000
analysis
- If you want to calculate every possible set , You need a backtracking algorithm , If only counting , Dynamic planning .
- Abstract problem : Completely backpack ( Because a number can be taken many times )
- Find the total number : Combination question ,
dp[j] = dp[j-nums[i]] - initialization :
dp[0] = 1 - traversal order , Double forward , Order doesn't matter
- dp[j] Express : Capacity of j My backpack has dp[j] A way to fill your backpack
Code
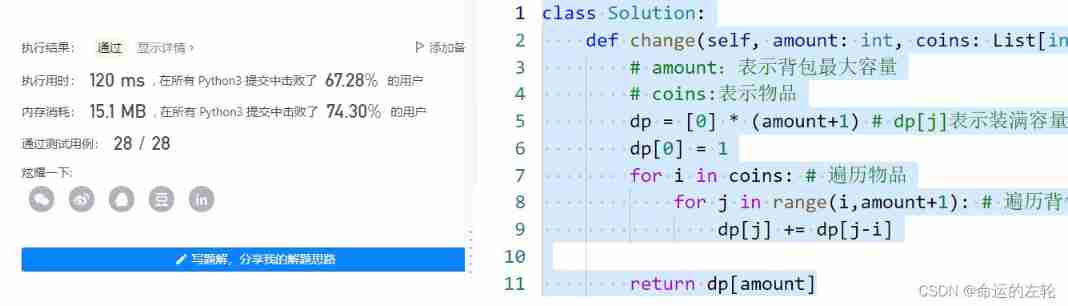
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
# amount: Indicates the maximum capacity of the backpack
# coins: Indicates an item
dp = [0] * (amount+1) # dp[j] Indicates that the full capacity is j The possibility of backpacking
dp[0] = 1
for i in coins: # Traverse the items
for j in range(i,amount+1): # Traverse the backpack
dp[j] += dp[j-i]
return dp[amount]
Through screenshots
377. Combinatorial summation Ⅳ
Here you are Different An array of integers nums , And a target integer target . Please start from nums Find and return the sum of target The number of element combinations of .
The data of the questions ensure that the answers are in line with 32 Bit integer range .
Example 1:
Input :nums = [1,2,3], target = 4
Output :7
explain :
All possible combinations are :
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Please note that , Different sequences are considered as different combinations .
Example 2:
Input :nums = [9], target = 3
Output :0
Tips :
1 <= nums.length <= 200
1 <= nums[i] <= 1000
nums All elements in Different from each other
1 <= target <= 1000
analysis
- Abstract problem : Completely backpack ( Because a number can be taken many times )
- Find the total number : Here is the case output , Knowing is a permutation problem
- initialization :
dp[0] = 1 - traversal order , We said that the complete knapsack problem is generally double positive order , There is no difference between the inner and outer layers of items and backpacks . however , In this question , The backpack must be on the outer layer , Items are inside . Think about it a little bit , Arrangement is the case of different order , If you put the object on the outer layer , Anyway, the order of items is fixed . So put the items on the inner layer , The item is traversed many times , In a different order .
- dp[j] Express : Capacity of j My backpack has dp[j] A way to fill your backpack .
- Because it is a forward traversal , Pay attention to the starting position , But since we started with backpacks , So I can't determine which position is more suitable at the beginning , So after the double cycle, we must judge the relationship between the size of the item and the backpack .
Code
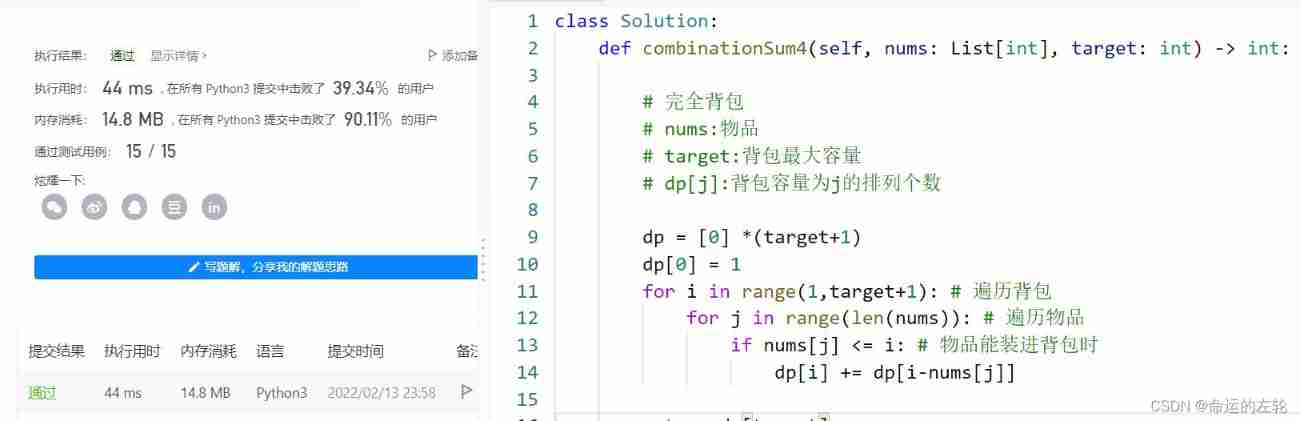
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
# Completely backpack
# nums: goods
# target: The maximum capacity of the backpack
# dp[j]: The capacity of the backpack is j Number of permutations of
dp = [0] *(target+1)
dp[0] = 1
for i in range(1,target+1): # Traverse the backpack
for j in range(len(nums)): # Traverse the items
if nums[j] <= i: # When items can be put into backpacks
dp[i] += dp[i-nums[j]]
return dp[target]
Through screenshots
If there is a mistake , Please correct me , Welcome to exchange , thank you *(・ω・)ノ
边栏推荐
- Face recognition 5- insight face padding code practice notes
- What is the difference between port mapping and port forwarding
- 如果炒股开华泰证券的户,在网上开户安全吗?
- JS how to realize array to tree
- 【selenium自动化】常用注解
- PermissionError: [Errno 13] Permission denied: ‘data. csv‘
- 同事的接口文档我每次看着就头大,毛病多多。。。
- [selenium automation] common notes
- A new method for analyzing the trend chart of London Silver
- 华为200万年薪聘请数据治理专家!背后的千亿市场值得关注
猜你喜欢
Date time type and format in MySQL
兩個數相互替換
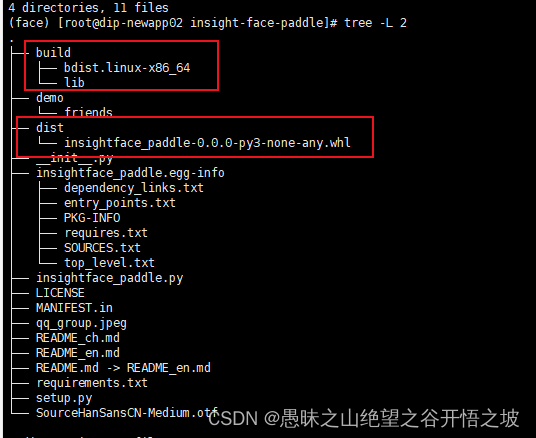
人脸识别5- insight-face-paddle-代码实战笔记
如何避免电弧产生?—— AAFD故障电弧探测器为您解决

如何有效对直流列头柜进行监测
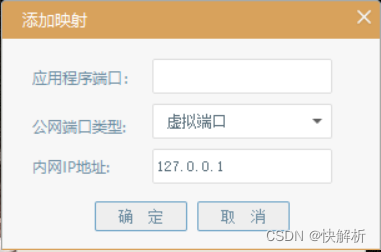
如何用快解析自制IoT云平台

abc 258 G - Triangle(bitset)
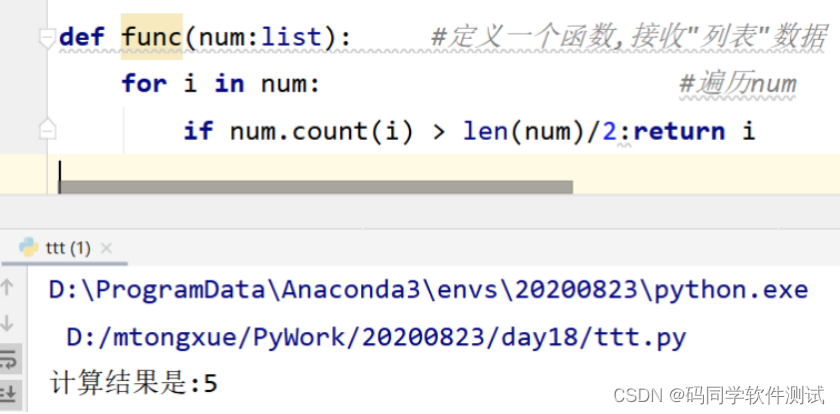
Tester's algorithm interview question - find mode
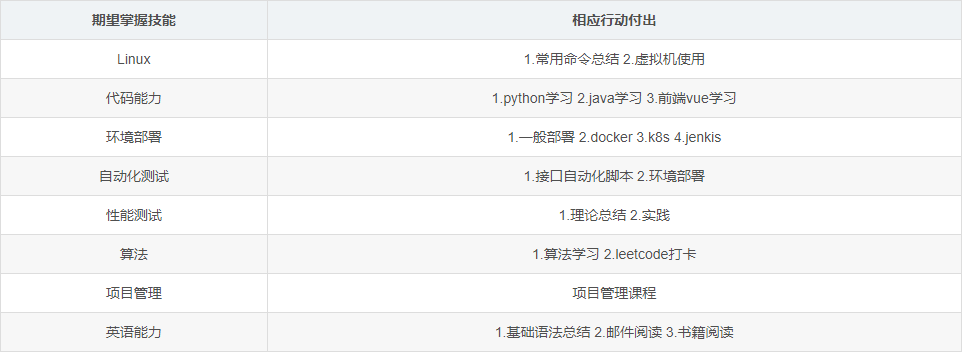
IT转测试岗,从迷茫到坚定我究竟付出了什么?
![[论文阅读] CarveMix: A Simple Data Augmentation Method for Brain Lesion Segmentation](/img/41/eb790e7419a158e985fa503bd7dc17.png)
[论文阅读] CarveMix: A Simple Data Augmentation Method for Brain Lesion Segmentation
随机推荐
[paper reading] Tun det: a novel network for meridian ultra sound nodule detection
C语言中sizeof操作符的坑
Fs8b711s14 electric wine bottle opener MCU IC scheme development special integrated IC
两个数相互替换
lambda表达式
JS convert pseudo array to array
Learning of basic amplification circuit
Illustrated network: what is gateway load balancing protocol GLBP?
IELTS examination process, what to pay attention to and how to review?
Go pit - no required module provides Package: go. Mod file not found in current directory or any parent
电力运维云平台:开启电力系统“无人值班、少人值守”新模式
Life is changeable, and the large intestine covers the small intestine. This time, I can really go home to see my daughter-in-law...
Summer challenge brings you to play harmoniyos multi terminal piano performance
Is it safe to open an account in the College of Finance and economics? How to open an account?
【C】(笔试题)指针与数组,指针
Continuous modification of business scenario functions
Detailed explanation of openharmony resource management
How to do the project of computer remote company in foreign Internet?
GDB common commands
Date time type and format in MySQL