当前位置:网站首页>AcWing 271. 杨老师的照相排列【多维DP】
AcWing 271. 杨老师的照相排列【多维DP】
2022-07-03 17:48:00 【Codiplay】
271. 杨老师的照相排列 - AcWing题库
题意:
在合影时要求每一排从左到右身高递减,每一列从后到前身高也递减。
问一共有多少种安排合影位置的方案
思路:

精华:
- 模拟操作,只有模拟出来操作,才知道对于当前这一步,应该由哪些步更新而来,你可以特殊化你的“每一步”,f也可以特殊化,因为你发现特殊化之后,找到代表的一些特性之后,缩减了原来的状态空间,但是答案所代表的空间还是在你特殊化后的状态空间里面,这样就能特殊化问题,通过大胆猜测和实践试错,抓住问题的本质。
- 集合:以数量这个性质来定义这个集合。为什么?因为在模拟的时候发现放当前这个数肯定是放在同一行的最左边,且上方不能有空格。
首先,1必须先放在左上角,其他数无法担任此重任。随后2必须在这两个位置,其他位置要么左侧有空格,要么上方有空格,不符合规定。所以,我们发现在放数的时候,甚至并不像最长上升子序列一样关心tail的值,因为题目本身就具有“单调性”,也就是说你只需要按照题目的意思模拟即可。
我们关心的是:当你要放当前这个数的时候,该集合的“形状”,即每一行的数量
- 题目给了特殊的k的范围,k最大是五层,特殊很小的范围和多维dp相关
- 初始化、循环拓扑更新的顺序问题。
f[0][0][0][0][0] = 1;对于这个题而言,任意一维取0,任意几维取0,哪一维取哪一维不取情况很多考虑起来非常麻烦,并且这些f都有实际意义,对应着实际情况,这个题就是从都为0一步步更新而来的,所以初始化只用初始化全为0的f即可。对于这种要从0开始的基本把0初始化为1,其他不用初始化。
既然从0开始下面的拓扑序也得对应相等。
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 31;
ll f[N][N][N][N][N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int n;
while(cin >> n, n) {
int s[5] = {0};
for (int i = 0; i < n; i ++ ) cin >> s[i];
memset(f, 0, sizeof f);
f[0][0][0][0][0] = 1;
//
for (int a = 0; a <= s[0]; a ++ ) {
for (int b = 0; b <= min(s[1], a); b ++ ) {
for (int c = 0; c <= min(s[2], b); c ++ ) {
for (int d = 0; d <= min(s[3], c); d ++ ) {
for (int e = 0; e <= min(s[4], d); e ++ ) {
ll &x = f[a][b][c][d][e];
if(a && a - 1 >= b) x += f[a - 1][b][c][d][e];
if(b && b - 1 >= c) x += f[a][b - 1][c][d][e];
if(c && c - 1 >= d) x += f[a][b][c - 1][d][e];
if(d && d - 1 >= e) x += f[a][b][c][d - 1][e];
if(e) x += f[a][b][c][d][e - 1];
}
}
}
}
}
cout << f[s[0]][s[1]][s[2]][s[3]][s[4]] << '\n';
}
return 0;
}边栏推荐
- Servlet specification Part II
- Where is the monitoring page of RDS database?
- 互联网医院HIS管理平台源码,在线问诊,预约挂号 智慧医院小程序源码
- What is the difference between cloud server and cloud virtual machine
- The difference between i++ and ++i: tell their differences easily
- Managing multiple selections with MVVM - managing multiple selections with MVVM
- 毕业总结
- Web-ui automated testing - the most complete element positioning method
- 自动渗透测试工具核心功能简述
- Golang单元测试、Mock测试以及基准测试
猜你喜欢

1146_ SiCp learning notes_ exponentiation
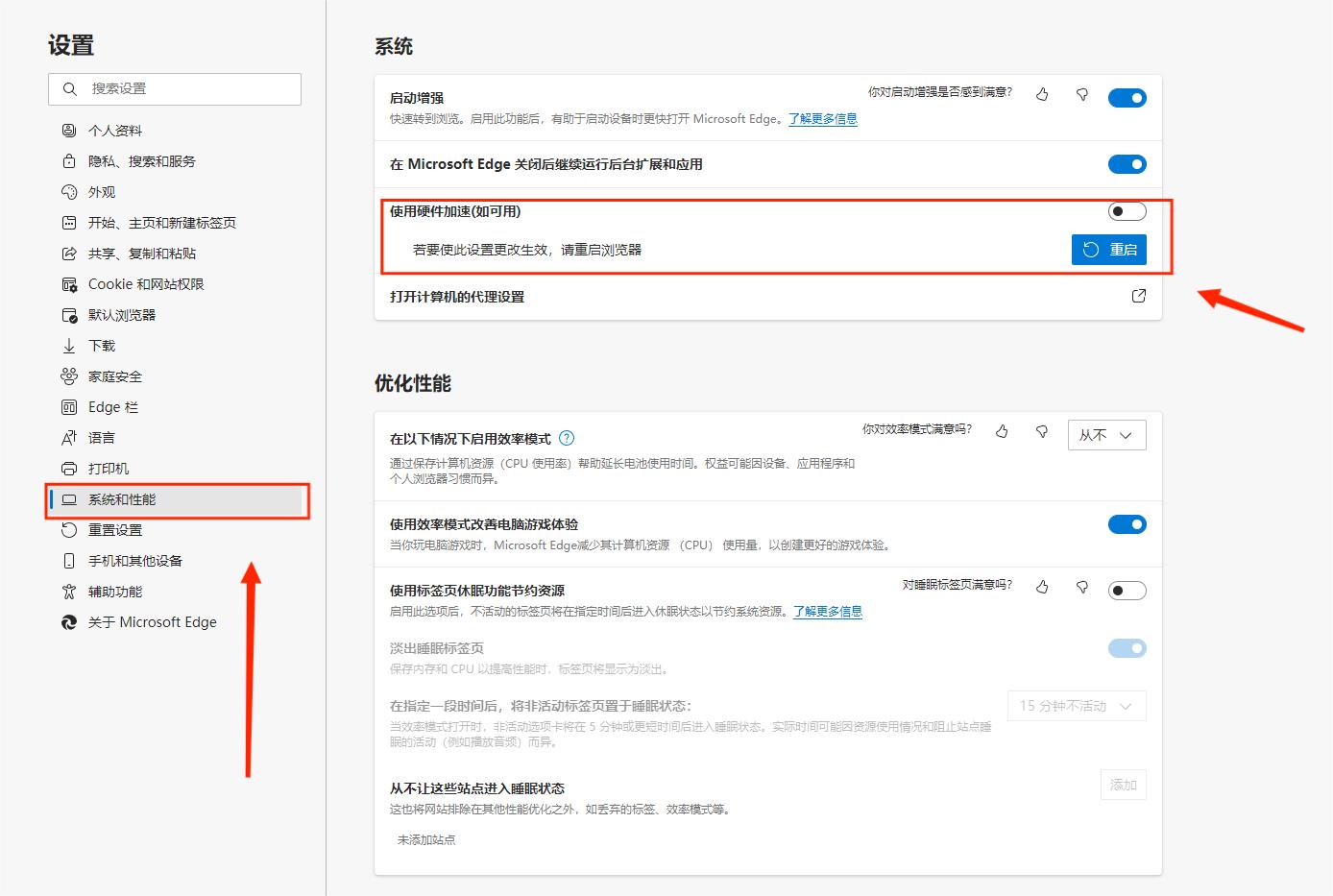
Notes on problems -- watching videos on edge will make the screen green

Select 3 fcpx plug-ins. Come and see if you like them

Global and Chinese health care OEM and ODM market status survey and investment planning recommendations report 2022-2028
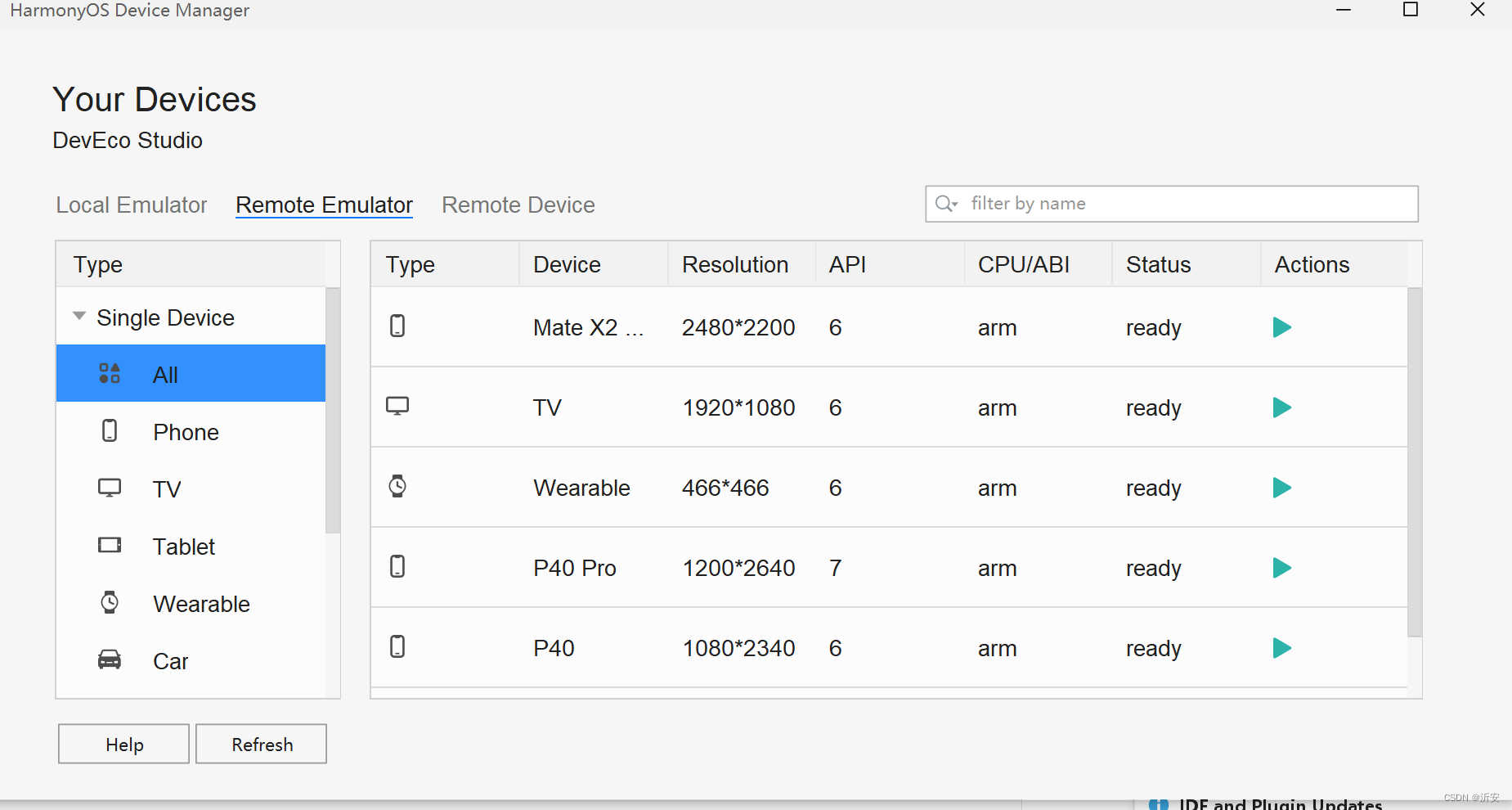
Hongmeng fourth training
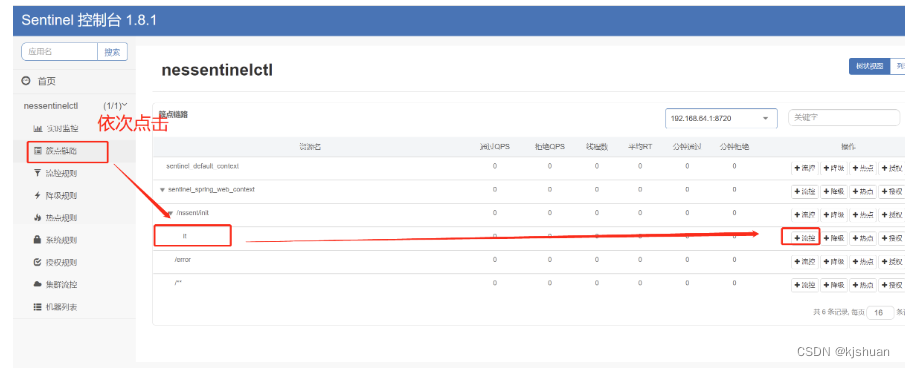
微服务组件Sentinel控制台调用
Qt调节Win屏幕亮度和声音大小
MySQL has been stopped in the configuration interface during installation

Implementation of Tetris in C language

How to deploy applications on kubernetes cluster
随机推荐
聊聊支付流程的设计与实现逻辑
小程序 多tab 多swiper + 每个tab分页
BFS - topology sort
毕业总结
Applet with multiple tabs and Swipers + paging of each tab
Micro service component sentinel console call
The third day of writing C language by Yabo people
List的stream中Long对象与long判等问题记录
WEB-UI自动化测试-最全元素定位方法
分布式的任务分发框架-Gearman
企业级自定义表单引擎解决方案(十一)--表单规则引擎1
Remote office tools sharing | community essay solicitation
Five problems of database operation in commodity supermarket system
i++与++i的区别:通俗易懂的讲述他们的区别
PHP processing - watermark images (text, etc.)
Life perception 1
The difference between i++ and ++i: tell their differences easily
PUT vs. POST for Uploading Files - RESTful API to be Built Using Zend Framework
[combinatorics] recursive equation (summary of the solution process of recursive equation | homogeneous | double root | non-homogeneous | characteristic root is 1 | exponential form | the bottom is th
Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028