[set theory] order relation (hastu example | divisive relation hastu | inclusive relation hastu | refinement relation hastu)

One 、 Hastu example ( Division relations )

---

aggregate

A

=

{

1

,

2

,

3

,

4

,

5

,

6

,

9

,

10

,

15

}

A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}

A={ 1,2,3,4,5,6,9,10,15} ,

aggregate

A

A

A On the division relationship “

∣

|

∣” It's a partial order relationship ,

Poset is

<

A

,

∣

>

<A, |>

<A,∣>

x

x

x to be divisible by

y

y

y ,

x

x

x It's a divisor ( The denominator ) ,

y

y

y It's a dividend ( molecular ) ;

y

x

\dfrac{y}{x}

xy​

y

y

y Can be

x

x

x to be divisible by ,

x

x

x It's a divisor ( The denominator ) ,

y

y

y It's a dividend ( molecular ) ;

y

x

\dfrac{y}{x}

xy​

Draw the above partially ordered set of hastu :

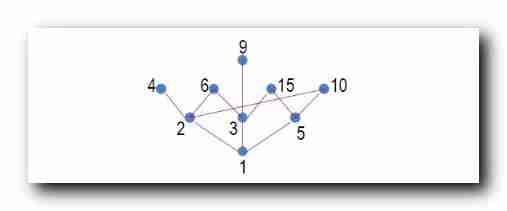
1

1

1 The smallest is the smallest ,

1

1

1 Can divide all numbers ;

1

1

1 The upper layer is prime , Prime numbers can only be

1

1

1 Divide by itself ; Primes must be covering

1

1

1 Of ; That is, prime numbers and

1

1

1 There are no elements between ;

Number above prime , Composed of numbers multiplied by prime numbers ;

6

6

6 It can be divisible

2

2

2 , It can also be divided

3

3

3 , Therefore, it covers

2

2

2 , And cover

3

3

3 ;

10

10

10 It can be divisible

2

2

2 , It can also be divided

5

5

5 , Therefore, it covers

2

2

2 , And cover

5

5

5 ;

15

15

15 It can be divisible

3

3

3 , It can also be divided

5

5

5 , Therefore, it covers

3

3

3 , And cover

5

5

5 ;

4

4

4 Divisibility

2

2

2 , therefore

4

4

4 Cover

2

2

2 ;

9

9

9 Divisibility

3

3

3 , therefore

9

9

9 Cover

3

3

3 ;

Two 、 Hastu example ( Inclusion relation )

---

aggregate

A

=

{

a

,

b

,

c

}

A = \{ a, b , c \}

A={ a,b,c} ,

Set family

A

\mathscr{A}

A Included in

A

A

A The power set of a set ,

A

⊆

P

(

A

)

\mathscr{A} \subseteq P(A)

A⊆P(A) ,

Set family

A

=

{

∅

,

{

a

}

,

{

b

}

,

{

c

}

,

{

a

,

b

}

,

{

b

,

c

}

,

{

a

,

c

}

}

\mathscr{A} = \{ \varnothing , \{ a \} , \{ b \} , \{ c \} , \{ a , b \} , \{ b,c \} , \{ a, c \} \}

A={ ∅,{ a},{ b},{ c},{ a,b},{ b,c},{ a,c}}

Set family

A

\mathscr{A}

A Upper Inclusion relation “

⊆

\subseteq

⊆” It's a partial order relationship ,

Poset is

<

A

,

⊆

>

<\mathscr{A} , \subseteq >

<A,⊆>

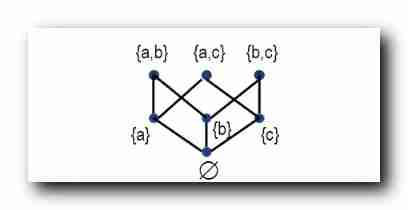
An empty set Included in All sets , The smallest is the smallest , At the bottom of hasstu ;

An empty set Above is the unit set , Unit set Cover An empty set , There is no third element between them ;

There is no inclusive relationship between the three unit sets , Is incomparable ;

Unit set Above all Binary set , Every Binary set Below is the corresponding unit set it contains ;

3、 ... and 、 Hastu example ( Refinement relation )

---

Refinement relation yes Ordered pair set , Each of them Elements of ordered pairs yes Set family ;

aggregate

A

A

A Non empty ,

π

\pi

π yes

A

A

A Set divided into sets , Every partition is a set family ;

Divide reference : 【 Set theory 】 Divide ( Divide | Partition example | Partition and equivalence )

There is a relationship between sets , Refinement relation , Using symbols

≼

Add

fine

\preccurlyeq_{ Refine }

≼ Add fine ​ Express ;

Refinement relation

≼

Add

fine

\preccurlyeq_{ Refine }

≼ Add fine ​ Symbolize :

≼

Add

fine

=

{

<

x

,

y

>

∣

x

,

y

∈

π

∧

x

yes

y

Of

Add

fine

}

\preccurlyeq_{ Refine } = \{ <x, y> | x, y \in \pi \land x yes y The refinement of \}

≼ Add fine ​={ <x,y>∣x,y∈π∧x yes y Of Add fine }

Premise :

• aggregate

  A

  =

  {

  a

  ,

  b

  ,

  c

  ,

  d

  }

  A = \{ a, b , c , d \}

  A={ a,b,c,d}

• Set family

  A

  1

  =

  {

  {

  a

  }

  ,

  {

  b

  }

  ,

  {

  c

  }

  ,

  {

  d

  }

  }

  \mathscr{A}_1= \{ \{ a \} , \{ b \} , \{ c \} , \{ d \} \}

  A1​={ { a},{ b},{ c},{ d}}

• Set family

  A

  2

  =

  {

  {

  a

  ,

  b

  }

  ,

  {

  c

  ,

  d

  }

  }

  \mathscr{A}_2 = \{ \{ a , b \} , \{ c , d \} \}

  A2​={ { a,b},{ c,d}}

• Set family

  A

  3

  =

  {

  {

  a

  ,

  c

  }

  ,

  {

  b

  ,

  d

  }

  }

  \mathscr{A}_3= \{ \{ a,c \} , \{ b,d\} \}

  A3​={ { a,c},{ b,d}}

• Set family

  A

  4

  =

  {

  {

  a

  }

  ,

  {

  b

  ,

  c

  ,

  d

  }

  }

  \mathscr{A}_4= \{ \{ a \} , \{ b, c , d \} \}

  A4​={ { a},{ b,c,d}}

• Set family

  A

  5

  =

  {

  {

  a

  }

  ,

  {

  b

  }

  ,

  {

  c

  ,

  d

  }

  }

  \mathscr{A}_5= \{ \{ a \} , \{ b \} , \{ c , d \} \}

  A5​={ { a},{ b},{ c,d}}

• Set family

  A

  6

  =

  {

  {

  a

  ,

  b

  ,

  c

  ,

  d

  }

  }

  \mathscr{A}_6 = \{ \{ a , b , c , d\} \}

  A6​={ { a,b,c,d}}

The above families are

A

A

A Partition of sets ;

Hassu who divides the relationship :

A

1

\mathscr{A}_1

A1​ It is the refinement of all divisions , Is the most detailed division , At the bottom of hasstu ;

All the divisions are

A

6

\mathscr{A}_6

A6​ The refinement of , It is the coarsest division , At the top of hasstu ;

A

5

\mathscr{A}_5

A5​ both

A

2

\mathscr{A}_2

A2​ The refinement of , again

A

4

\mathscr{A}_4

A4​ The refinement of ;

A

3

\mathscr{A}_3

A3​ And

A

4

\mathscr{A}_4

A4​ Each other is not each other's refinement , There is no comparison ;

A

2

\mathscr{A}_2

A2​ And

A

4

\mathscr{A}_4

A4​ Each other is not each other's refinement , There is no comparison ;

A

2

\mathscr{A}_2

A2​ And

A

3

\mathscr{A}_3

A3​ Each other is not each other's refinement , There is no comparison ;

A

3

\mathscr{A}_3

A3​ And

A

5

\mathscr{A}_5

A5​ Each other is not each other's refinement , There is no comparison ;