当前位置:网站首页>蓝桥杯2022初赛——扫雷
蓝桥杯2022初赛——扫雷
2022-06-29 02:46:00 【疯疯癫癫才自由】
4407. 扫雷
小明最近迷上了一款名为《扫雷》的游戏。
其中有一个关卡的任务如下:
在一个二维平面上放置着 n
个炸雷,第 i 个炸雷 (xi,yi,ri) 表示在坐标 (xi,yi) 处存在一个炸雷,它的爆炸范围是以半径为 ri
的一个圆。
为了顺利通过这片土地,需要玩家进行排雷。
玩家可以发射 m
个排雷火箭,小明已经规划好了每个排雷火箭的发射方向,第 j 个排雷火箭 (xj,yj,rj) 表示这个排雷火箭将会在 (xj,yj) 处爆炸,它的爆炸范围是以半径为 rj
的一个圆,在其爆炸范围内的炸雷会被引爆。
同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆。
现在小明想知道他这次共引爆了几颗炸雷?
你可以把炸雷和排雷火箭都视为平面上的一个点。
一个点处可以存在多个炸雷和排雷火箭。
当炸雷位于爆炸范围的边界上时也会被引爆。
输入格式
输入的第一行包含两个整数 n、m
。
接下来的 n
行,每行三个整数 xi,yi,ri
,表示一个炸雷的信息。
再接下来的 m
行,每行三个整数 xj,yj,rj
,表示一个排雷火箭的信息。
输出格式
输出一个整数表示答案。
数据范围
对于 40%
的评测用例:0≤x,y≤109,0≤n,m≤103,1≤r≤10,
对于 100% 的评测用例:0≤x,y≤109,0≤n,m≤5×104,1≤r≤10
。
输入样例:
2 1
2 2 4
4 4 2
0 0 5
输出样例:
2
样例解释
示例图如下,排雷火箭 1
覆盖了炸雷 1,所以炸雷 1 被排除;炸雷 1 又覆盖了炸雷 2,所以炸雷 2
也被排除。

排雷火箭可以排掉地雷,地雷又可以排掉它能排掉范围内的地雷,所以显然是图的遍历问题。
可是,如果不对原始数据进行处理,直接用邻接表或者临界矩阵来建图,明显会超时。因为点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9。但是先把坐标按x轴从小到大排序,再按y轴从小到大排序,时间复杂度是O(nlgn),再加上建图的时间复杂度O(n*r),查询的时间复杂度O(m*lgn+n)。可以AC。
这道题我花了数日,研究了数种方法,有map解决,unordered_map解决,有手写hash表解决,能AC的BFS和DFS我都写出来了,不是y总讲的方法,便是在acwing上看到大佬写的代码,自己动手写了一遍。不言而喻,效率比较:手写hash > unordered_map > map,
不过话说回来,在这道题中让我学到的知识蛮不少的。
代码中我有一些调试的代码,我没删除,那一部分到也没必要看,我都注释掉了的。
一共十一种代码,能AC的倒没几种,不过在写的过程中,是满满的收获啊。学到了如何手写hash表,map和unorded_map的效率差别,知道了当自己写的结构体或者pair作为unordered_map的key值的时候,需要自己写一个函数来对他们排序,因为编译器无法知道他们的关系。当然这个函数要用类来封装。想必以后也能用上lower_bound()和upper_bound了吧。虽然都知道这些函数,但是不知道什么时候用,还是自己写的题目太少了。同志,革命尚未成功,吾得急需努力。
其实算法笔记讲解BFS的时候就已经强调了inq表示结点是否入队,而不是是否访问,否则就会存在多个点进行入队,这和DFS的vis数组是有区别的,当时还不以为然,觉得自己都理解了,现在想想,亦是惭愧!书你倒是看了,但你是否真正的吸收了呢?每学到一个算法,就要去找相应的题目来做,不然你也只是白白浪费时间,多了不说,算法笔记上的树状数组以及lowbit数组你现在是否还能知道它们的意思,KMP算法是否还有印象,快速排序是否还能写出来,组合数的知识还知道多少。。。等等,不光是低头做题,还得总结自己学到的东西,以后遇到能够用自己学过的算法解决的题目的时候,别两眼一蹬,我不会,毫无思路?那就从此处开始,把之前写的算法发成博客吧,也能再温习一遍。
万丈高楼平地起,莫在浮沙筑高台!
第一种,图的深度优先遍历,邻接表实现, 由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9, 明显会超时。
/**
图的深度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
明显会超时
*/
/**
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
using namespace std;
const int maxn=1010;
struct Node
{
int x,y,r;
}cir[maxn];
vector<int> adj[maxn];
bool vis[maxn]={false};
int n,m;
int dfs_Trave(int x,int y,int r);
int dfs(int index);
void add(int index);
int main()
{
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
}
for(int i=0;i<n;++i)
{
add(i);
}
// cout << "调试:\n";
// for(int i=0;i<n;++i)
// {
// for(auto b:adj[i])
// cout << b << ' ';
// cout << endl;
// }
// cout << "jk\n";
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
// cout << "r:" << r << endl;
//printf("r:%d\n",r);
res+=dfs_Trave(x,y,r);
}
printf("%d\n",res);
return 0;
}
void add(int index)
{
for(int i=0;i<n;++i)
if(i!=index)
{
if(cir[index].r>(sqrt(pow(cir[i].x-cir[index].x,2)+pow(cir[i].y-cir[index].y,2))))
adj[index].push_back(i);
}
}
int dfs(int index)
{
//cout << "jinbulai?\n";
int sum=1;
vis[index]=true;
for(int i=0;i<adj[index].size();++i)
{
int v=adj[index][i];
if(vis[v]==false)
sum+=dfs(v);
}
return sum;
}
int dfs_Trave(int x,int y,int r)
{
// cout << "r:" << r << endl;
int sum=0;
for(int i=0;i<n;++i)
{
double L=sqrt(pow(x-cir[i].x,2)+pow(y-cir[i].y,2));
// cout << "length:" << L << endl;
if(r>L)
{
// cout << "error: \n";
if(vis[i]==false)
sum+=dfs(i);
}
}
return sum;
}第二种, 图的深度优先遍历,邻接表实现,由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,先把坐标按x轴从小到大排序,再按y轴从小到大排序, acwing 最后一组数据通不过,最开始的时候始终找不出原因,现在想想,也能理解,
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
下一个代码我给出了AC的代码;
*/
/**
图的深度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
acwing 最后一组数据通不过,最开始的时候始终找不出原因,现在想想,也能理解,
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
下一个代码我给出了AC的代码;
*/
/**
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
#include <unordered_map>
using namespace std;
const int maxn=50010;
struct Node
{
int x,y,r;
int cnt;
Node (int _x,int _y) : x(_x),y(_y){}
Node (int _x,int _y,int _r) : x(_x),y(_y),r(_r){}
Node (int _x,int _y,int _r,int _cnt) :x(_x),y(_y),r(_r),cnt(_cnt){}
Node()=default;
bool operator < (Node const & a) const
{
if(x!=a.x)
return x<a.x;
return y<a.y;
}
}cir[maxn];
struct comp
{
int operator()(const std::pair<int, int>& p) const {
return p.first ^ p.second; //返回值为bool,比较符为&,|都比这一个慢,
}
};
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
vector<int> adj[maxn];
unordered_map<pair<int,int> ,int,comp> ump;
bool vis[maxn]={false};
int n,m;
int dfs_Trave(int x,int y,int r);
int dfs(int index);
void add(int index);
int main()
{
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=1;i<=n;++i)
{
scanf("%d%d%d",&x,&y,&r);
auto temp=ump[{x,y}];
if(temp!=0)
{
cir[temp].r=max(cir[temp].r,r);
cir[temp].cnt++;
}
else
{
cir[i]={x,y,r,1}; //应当用一个全局变量来表示不重复点的下标
ump[{x,y}]=i; //
}
}
sort(cir+1,cir+n+1);
// Node temp={2,3,9};
// auto it=lower_bound(cir+1,cir+n+1,temp);
// cout << "tiaoshi: " << it->x << ' ' << it->y << ' ' << it->r << endl;
// Node temp2={2,50,9};
// it=lower_bound(cir+1,cir+n+1,temp2);
// cout << "tiaoshi: " << it->x << ' ' << it->y << ' ' << it->r << endl;
// cout << "调试:\n";
// for(int i=1;i<=n;++i)
// cout << cir[i].x << ' ' << cir[i].y << ' ' << cir[i].r << endl;
// cout << "ok\n";
for(int i=1;i<=n;++i)
{
add(i);
}
// cout << "调试:\n";
// for(int i=0;i<n;++i)
// {
// for(auto b:adj[i])
// cout << b << ' ';
// cout << endl;
// }
// cout << "jk\n";
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
// cout << "r:" << r << endl;
//printf("r:%d\n",r);
res+=dfs_Trave(x,y,r);
}
printf("%d\n",res);
return 0;
}
void add(int index)
{
for(int i=index-1;i>0;--i)
{
if(squ(cir[index].r)<squ(cir[i].x-cir[index].x))
break;
if(squ(cir[index].r)>=squ(cir[i].x-cir[index].x)+squ(cir[i].y-cir[index].y))
adj[index].push_back(i);
}
for(int i=index+1;i<=n;++i)
{
if(squ(cir[index].r) < squ(cir[i].x-cir[index].x))
break;
if(squ(cir[index].r) >= squ(cir[i].x-cir[index].x)+squ(cir[i].y-cir[index].y))
adj[index].push_back(i);
}
}
int dfs(int index)
{
int sum=cir[index].cnt;
vis[index]=1;
for(int i=0;i<adj[index].size();++i)
{
int v=adj[index][i];
if(vis[v]==0)
sum+=dfs(v);
}
return sum;
}
int dfs_Trave(int x,int y,int r)
{
Node e1={x-r,y,r},e2={x+r,y,r};
int l=lower_bound(cir+1,cir+n+1,e1)-cir;
int ri=lower_bound(cir+1,cir+n+1,e2)-cir;
l=min(l,n),ri=min(ri,n);
int sum=0;
for(int i=l;i<=ri;++i)
{
if(i==0)
continue;
if((squ(r)>=squ(cir[i].x-x)+squ(cir[i].y-y))&&vis[i]==0)
sum+=dfs(i);
}
return sum;
}第三个,/**
图的深度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
能AC
/**
图的深度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
能AC
*/
/**
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
#include <unordered_map>
using namespace std;
const int maxn=50010;
struct Node
{
int x,y,r;
int cnt;
Node (int _x,int _y) : x(_x),y(_y){}
Node (int _x,int _y,int _r) : x(_x),y(_y),r(_r){}
Node (int _x,int _y,int _r,int _cnt) :x(_x),y(_y),r(_r),cnt(_cnt){}
Node()=default;
bool operator < (Node const & a) const
{
if(x!=a.x)
return x<a.x;
return y<a.y;
}
}cir[maxn];
struct comp
{
int operator()(const std::pair<int, int>& p) const {
return p.first ^ p.second; //返回值为bool,比较符为&,|都比这一个慢,
}
};
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
vector<int> adj[maxn];
unordered_map<pair<int,int> ,int,comp> ump; //实践上机证明将坐标转化为long long 比这种方式快上一点
bool vis[maxn]={false};
int n,m,n1=0;
int dfs_Trave(int x,int y,int r);
int dfs(int index);
void add(int index);
int main()
{
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=1;i<=n;++i)
{
scanf("%d%d%d",&x,&y,&r);
auto temp=ump[{x,y}];
if(temp!=0)
{
cir[temp].r=max(cir[temp].r,r);
cir[temp].cnt++;
}
else
{
cir[++n1]={x,y,r,1};
ump[{x,y}]=n1;
// cir[i].cnt=1;
}
}
sort(cir+1,cir+n1+1);
// Node temp={2,3,9};
// auto it=lower_bound(cir+1,cir+n+1,temp);
// cout << "tiaoshi: " << it->x << ' ' << it->y << ' ' << it->r << endl;
// Node temp2={2,50,9};
// it=lower_bound(cir+1,cir+n+1,temp2);
// cout << "tiaoshi: " << it->x << ' ' << it->y << ' ' << it->r << endl;
// cout << "调试:\n";
// for(int i=1;i<=n;++i)
// cout << cir[i].x << ' ' << cir[i].y << ' ' << cir[i].r << endl;
// cout << "ok\n";
for(int i=1;i<=n1;++i)
{
add(i);
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
res+=dfs_Trave(x,y,r);
}
printf("%d\n",res);
return 0;
}
void add(int index)
{
for(int i=index-1;i>0;--i)
{
if(squ(cir[index].r)<squ(cir[i].x-cir[index].x))
break;
if(squ(cir[index].r)>=squ(cir[i].x-cir[index].x)+squ(cir[i].y-cir[index].y))
adj[index].push_back(i);
}
for(int i=index+1;i<=n1;++i)
{
if(squ(cir[index].r) < squ(cir[i].x-cir[index].x))
break;
if(squ(cir[index].r) >= squ(cir[i].x-cir[index].x)+squ(cir[i].y-cir[index].y))
adj[index].push_back(i);
}
}
int dfs(int index)
{
int sum=cir[index].cnt;
vis[index]=1;
for(int i=0;i<adj[index].size();++i)
{
int v=adj[index][i];
if(vis[v]==0)
sum+=dfs(v);
}
return sum;
}
int dfs_Trave(int x,int y,int r)
{
Node e1={x-r,y,r},e2={x+r,y,r};
int l=lower_bound(cir+1,cir+n1+1,e1)-cir;
int ri=lower_bound(cir+1,cir+n1+1,e2)-cir;
l=min(l,n1),ri=min(ri,n1);
int sum=0;
for(int i=l;i<=ri;++i)
{
if(i==0)
continue;
if((squ(r)>=squ(cir[i].x-x)+squ(cir[i].y-y))&&vis[i]==0)
sum+=dfs(i);
}
return sum;
}第四个, 图的广度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
能AC
/**
图的广度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
能AC
*/
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
const int maxn=50010;
struct Node
{
int x,y,r;
int cnt;
Node (int _x,int _y) : x(_x),y(_y){}
Node (int _x,int _y,int _r) : x(_x),y(_y),r(_r){}
Node (int _x,int _y,int _r,int _cnt) :x(_x),y(_y),r(_r),cnt(_cnt){}
Node()=default;
bool operator < (Node const & a) const
{
if(x!=a.x)
return x<a.x;
return y<a.y;
}
}cir[maxn];
struct comp
{
int operator()(const std::pair<int, int>& p) const {
return p.first ^ p.second; //返回值为bool,比较符为&,|都比这一个慢,
}
};
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
vector<int> adj[maxn];
unordered_map<pair<int,int> ,int,comp> ump; //实践上机证明将坐标转化为long long 比这种方式快上一点
bool vis[maxn]={false};
int n,m,n1=0;
int bfs_Trave(int x,int y,int r);
int bfs(int index);
void add(int index);
int main()
{
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=1;i<=n;++i)
{
scanf("%d%d%d",&x,&y,&r);
auto temp=ump[{x,y}];
if(temp!=0)
{
cir[temp].r=max(cir[temp].r,r);
cir[temp].cnt++;
}
else
{
cir[++n1]={x,y,r,1};
ump[{x,y}]=n1;
// cir[i].cnt=1;
}
}
sort(cir+1,cir+n1+1);
// Node temp={2,3,9};
// auto it=lower_bound(cir+1,cir+n+1,temp);
// cout << "tiaoshi: " << it->x << ' ' << it->y << ' ' << it->r << endl;
// Node temp2={2,50,9};
// it=lower_bound(cir+1,cir+n+1,temp2);
// cout << "tiaoshi: " << it->x << ' ' << it->y << ' ' << it->r << endl;
// cout << "调试:\n";
// for(int i=1;i<=n;++i)
// cout << cir[i].x << ' ' << cir[i].y << ' ' << cir[i].r << endl;
// cout << "ok\n";
for(int i=1;i<=n1;++i)
{
add(i);
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
res+=bfs_Trave(x,y,r);
}
printf("%d\n",res);
return 0;
}
void add(int index)
{
for(int i=index-1;i>0;--i)
{
if(squ(cir[index].r)<squ(cir[i].x-cir[index].x))
break;
if(squ(cir[index].r)>=squ(cir[i].x-cir[index].x)+squ(cir[i].y-cir[index].y))
adj[index].push_back(i);
}
for(int i=index+1;i<=n1;++i)
{
if(squ(cir[index].r) < squ(cir[i].x-cir[index].x))
break;
if(squ(cir[index].r) >= squ(cir[i].x-cir[index].x)+squ(cir[i].y-cir[index].y))
adj[index].push_back(i);
}
}
int bfs(int index)
{
queue<int> q;
q.push(index);
int sum=cir[index].cnt;
while(!q.empty())
{
int top=q.front();
q.pop();
for(int i=0;i<adj[top].size();++i)
{
int v=adj[top][i];
if(vis[v]==0)
{
vis[v]=1;
sum+=cir[v].cnt;
q.push(v);
}
}
}
return sum;
}
int bfs_Trave(int x,int y,int r)
{
Node e1={x-r,y,r},e2={x+r,y,r};
int l=lower_bound(cir+1,cir+n1+1,e1)-cir;
int ri=lower_bound(cir+1,cir+n1+1,e2)-cir;
l=min(l,n1),ri=min(ri,n1);
int sum=0;
for(int i=l;i<=ri;++i)
{
if(i==0)
continue;
if((squ(r)>=squ(cir[i].x-x)+squ(cir[i].y-y))&&vis[i]==0)
{
vis[i]=1;
sum+=bfs(i);
}
}
return sum;
}第五个,/**
map,将坐标用pair<int,int>存在map中
*/
/**
1)每输入一个排雷火箭,就算出它排掉了多少雷,但是由于一个位置有多个雷
,所以要把这个位置的地雷数给记录下来;
acwing通过5/11
*/
/**
map,将坐标用pair<int,int>存在map中
*/
/**
1)每输入一个排雷火箭,就算出它排掉了多少雷,但是由于一个位置有多个雷
,所以要把这个位置的地雷数给记录下来;
acwing通过5/11
*/
/**
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <map>
using namespace std;
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
map<pair<int,int>,pair<int,int> > mp;
map<pair<int,int>,int > vis;
int n,m;
int dfs_Trave(int x,int y,int r);
int dfs(pair<pair<int,int>,pair<int,int> > index);
int main()
{
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
auto temp=make_pair(x,y);
auto it=mp.find(temp);
if(it==mp.end())
{
vis[temp]=0;
auto val=make_pair(r,1);
mp[temp]=val;
}
else
{
if(r>it->second.first)
{
auto val=make_pair(r,it->second.second+1);
mp[temp]=val;
}
else
{
auto val=make_pair(it->second.first,it->second.second+1);
mp[temp]=val;
}
}
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
res+=dfs_Trave(x,y,r);
}
printf("%d\n",res);
return 0;
}
int dfs(pair<pair<int,int>,pair<int,int> > index)
{
int x=index.first.first,y=index.first.second,r=index.second.first,num=index.second.second;
int sum=num;
//cout << "调试:" << sum << endl;
vis[index.first]=1;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
sum+=dfs(*it);
}
}
}
return sum;
}
int dfs_Trave(int x,int y,int r)
{
int sum=0;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
sum+=dfs(*it);
}
}
}
return sum;
}
*/
第六个,/**
2)先把排掉的雷给记录下来,最后统一计算,只记录半径,不用记录每个位置有多少雷;
当相应的就需要把所有的地雷的位置给记录下来,即使他们是相同的位置这就是cir数组的作用
acwing也是通过5/11
*/
/**
2)先把排掉的雷给记录下来,最后统一计算,只记录半径,不用记录每个位置有多少雷;
当相应的就需要把所有的地雷的位置给记录下来,即使他们是相同的位置这就是cir数组的作用
acwing也是通过5/11
*/
/**
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <map>
using namespace std;
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
const int maxn=50010;
struct Node
{
int x,y,r;
}cir[maxn];
map<pair<int,int>,int > mp;
map<pair<int,int>,int > vis;
int n,m;
void dfs_Trave(int x,int y,int r);
void dfs(pair<pair<int,int>,int > index);
int main()
{
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
auto temp=make_pair(x,y);
auto it=mp.find(temp);
if(it==mp.end())
{
vis[temp]=0;
mp[temp]=r;
}
else
{
if(r>it->second)
mp[temp]=r;
}
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
dfs_Trave(x,y,r);
}
for(int i=0;i<n;++i)
{
auto temp=make_pair(cir[i].x,cir[i].y);
if(vis[temp]!=0)
++res;
}
printf("%d\n",res);
return 0;
}
void dfs(pair<pair<int,int>,int > index)
{
int x=index.first.first,y=index.first.second,r=index.second;
vis[index.first]=1;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(*it);
}
}
}
}
void dfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(*it);
}
}
}
}
*/第七个,/**
unorder_map解决,将坐标用pair<int,int>存在unordered_map中
*/
/**
1)对于没有默认的哈希函数的类型,如自定义的 class 类型,pair 类型等,我们就必须自己
指定一个哈希函数。这也是为什么直接构建 pair 类型的 unordered_set
如 unordered_set<pair<int, int>> uset 会出现问题
acwing通过5/11
*/
/**
unorder_map解决,将坐标用pair<int,int>存在unordered_map中
*/
/**
1)对于没有默认的哈希函数的类型,如自定义的 class 类型,pair 类型等,我们就必须自己
指定一个哈希函数。这也是为什么直接构建 pair 类型的 unordered_set
如 unordered_set<pair<int, int>> uset 会出现问题
acwing通过5/11
*/
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <unordered_map>
using namespace std;
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
const int maxn=50010;
/*
struct cmp
{
bool operator()(pair<int,int> const &p) const
{
return p.first<p.second;
}
};
*/
//struct cmp
//{
// std::size_t operator()(const std::pair<int, int>& p) const {
// return p.first ^ p.second;
// }
//};
struct cmp
{
int operator()(const std::pair<int, int>& p) const {
return p.first ^ p.second; //返回值为bool,比较符为&,|都比这一个慢,
}
};
struct Node
{
int x,y,r;
}cir[maxn];
unordered_map<pair<int,int>,int ,cmp> mp;
unordered_map<pair<int,int>,int ,cmp> vis;
int n,m;
void dfs_Trave(int x,int y,int r);
void dfs(pair<pair<int,int>,int > index);
int main()
{
// int a=123456789,b=123456;
// int c=a&b;
// cout << c << endl;
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
auto temp=make_pair(x,y);
auto it=mp.find(temp);
if(it==mp.end())
{
vis[temp]=0;
mp[temp]=r;
}
else
{
if(r>it->second)
mp[temp]=r;
}
}
/*
cout << "调试:\n";
for(auto val:mp)
cout << val.first.first << ' ' << val.first.second << ' ' << val.second << endl;
*/
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
dfs_Trave(x,y,r);
}
for(int i=0;i<n;++i)
{
auto temp=make_pair(cir[i].x,cir[i].y);
if(vis[temp]!=0)
++res;
}
printf("%d\n",res);
return 0;
}
void dfs(pair<pair<int,int>,int > index)
{
int x=index.first.first,y=index.first.second,r=index.second;
vis[index.first]=1;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(*it);
}
}
}
}
void dfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=make_pair(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(*it);
}
}
}
}第八个,/**
将坐标转换为一个long long数值,存在unorder_map中;
acwing通过了6/11;
*/
/**
将坐标转换为一个long long数值,存在unorder_map中;
acwing通过了6/11;
*/
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <string>
#include <unordered_map>
using namespace std;
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
const int maxn=50010,inf=1e9;
LL hash_val(int x,int y)
{
return x*(inf+1ll)+y;
}
/*
struct cmp
{
bool operator()(pair<int,int> const &p) const
{
return p.first<p.second;
}
};
*/
//struct cmp
//{
// std::size_t operator()(const std::pair<int, int>& p) const {
// return p.first ^ p.second;
// }
//};
//struct cmp
//{
// int operator()(const LL, int>& p) const {
// return p.first < p.second;
// }
//};
//struct Node
//{
// int x,y,r;
//}cir[maxn];
vector<LL> cir;
unordered_map<LL,int> mp;
unordered_map<LL,int> vis;
int n,m;
void dfs_Trave(int x,int y,int r);
void dfs(int x,int y,int r);
int main()
{
// int a=123456789,b=123456;
// int c=a&b;
// cout << c << endl;
// int a=123456789,b=45612;
// cout << hash_val(a,b) << endl;
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
//cir[i]={x,y,r};
LL temp=hash_val(x,y);
//string temp=to_string(val);
cir.push_back(temp);
// mp[temp]=r;
// vis[temp]=0;
auto it=mp.find(temp);
if(it==mp.end())
{
vis[temp]=0;
mp[temp]=r;
}
else
{
if(r>it->second)
mp[temp]=r;
}
}
// cout << "调试:\n";
// for(auto val:mp)
// cout << val.first << ' ' << val.second << endl;
// cout << "\ntiaoshi\n";
// for(auto a:vis)
// cout << a.first << ' ' << a.second << endl;
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
dfs_Trave(x,y,r);
}
// cout << "\ntiaoshi2:\n";
// for(auto a:vis)
// cout << a.first << ' ' << a.second << endl;
for(int i=0;i<n;++i)
{
auto temp=cir[i];
if(vis[temp]!=0)
++res;
}
printf("%d\n",res);
return 0;
}
void dfs(int x,int y,int r)
{
LL val=hash_val(x,y);
// int x=index.first.first,y=index.first.second,r=index.second;
vis[val]=1;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
auto temp=hash_val(l,s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(l,s,it->second);
}
}
}
}
void dfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
LL temp=hash_val(l,s);
//string temp=to_string(val);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(l,s,it->second);
}
}
}
}
第九个,
/**
将坐标转换为string,存在unordered_map中
在acwing只能过4/11;
*/
/**
将坐标转换为string,存在unordered_map中
在acwing只能过4/11;
*/
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <string>
#include <unordered_map>
using namespace std;
typedef long long LL;
LL squ(int x)
{
return (LL) x*x;
}
const int maxn=50010,inf=1e9;
LL hash_val(int x)
{
return x*(inf+1ll);
}
/*
struct cmp
{
bool operator()(pair<int,int> const &p) const
{
return p.first<p.second;
}
};
*/
//struct cmp
//{
// std::size_t operator()(const std::pair<int, int>& p) const {
// return p.first ^ p.second;
// }
//};
//struct cmp
//{
// int operator()(const LL, int>& p) const {
// return p.first < p.second;
// }
//};
//struct Node
//{
// int x,y,r;
//}cir[maxn];
vector<string> cir;
unordered_map<string,int> mp;
unordered_map<string,int> vis;
int n,m;
void dfs_Trave(int x,int y,int r);
void dfs(int x,int y,int r);
int main()
{
// int a=123456789,b=123456;
// int c=a&b;
// cout << c << endl;
// int a=123456789,b=45612;
// cout << hash_val(a,b) << endl;
// int a=122,b=456;
// string s=to_string(a) +' ' +to_string(b);
// cout << s << endl;
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
//cir[i]={x,y,r};
LL val=hash_val(x);
string temp=to_string(val)+' ' +to_string(y);
cir.push_back(temp);
// mp[temp]=r;
// vis[temp]=0;
auto it=mp.find(temp);
if(it==mp.end())
{
vis[temp]=0;
mp[temp]=r;
}
else
{
if(r>it->second)
mp[temp]=r;
}
}
// cout << "调试:\n";
// for(auto val:mp)
// cout << val.first << ' ' << val.second << endl;
// cout << "\ntiaoshi\n";
// for(auto a:vis)
// cout << a.first << ' ' << a.second << endl;
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
dfs_Trave(x,y,r);
}
// cout << "\ntiaoshi2:\n";
// for(auto a:vis)
// cout << a.first << ' ' << a.second << endl;
for(int i=0;i<n;++i)
{
auto temp=cir[i];
if(vis[temp]!=0)
++res;
}
printf("%d\n",res);
return 0;
}
void dfs(int x,int y,int r)
{
LL val=hash_val(x);
string temp=to_string(val) +' ' + to_string(y);
// int x=index.first.first,y=index.first.second,r=index.second;
vis[temp]=1;
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
LL val=hash_val(l);
string temp=to_string(val)+' ' +to_string(s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(l,s,it->second);
}
}
}
}
void dfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l)
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
LL val=hash_val(l);
string temp=to_string(val)+' ' + to_string(s);
auto it=mp.find(temp);
if(it!=mp.end())
{
if(vis[temp]==0)
dfs(l,s,it->second);
}
}
}
}
第十个,/**
dfs实现图的遍历
手写hash表:把每个点唯一表示一个值,然后存到一个数组中,由于最大值为1e9,
所以可以把x坐标乘以一个(1e9+1)+y的坐标表示一个long long 值,也不会溢出,
即表示为一个两位的进制数,不过这个进制是1e9+1;
能AC;
*/
/**
dfs实现图的遍历
手写hash表:把每个点唯一表示一个值,然后存到一个数组中,由于最大值为1e9,
所以可以把x坐标乘以一个(1e9+1)+y的坐标表示一个long long 值,也不会溢出,
即表示为一个两位的进制数,不过这个进制是1e9+1;
能AC;
*/
#include <iostream>
#include <cstdio>
#include <vector>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=1e9,mod=7000003;
int test=999997; //测试数是否为素数
typedef long long LL;
struct Node
{
int x,y,r;
}cir[mod];
LL hs[mod]={0};
int id[mod]={0},vis[mod]={0};
int m,n;
void dfs(int x,int y,int r);
void dfs_Trave(int x,int y,int r);
LL hash_val(int x,int y) //将二维坐标转换为一个hash值
{
return (maxn+1ll)*x+y;
}
int hash_key(int x,int y)
{
LL val=hash_val(x,y);
int k=1,flag=-1;
int key=(val%mod+mod)%mod;
while(hs[key]!=-1&&hs[key]!=val) //此处需要hs[key]!=key,因为后面需要查找用到二维坐标,
{ //返回一个key值
key+=k*k*flag; //由于一个坐标最开始对应的key值也许被其他坐标占用了,这就需要查找
++k; //一个没被用到的值,但考虑到一个值一个值的加,元素容易扎堆都被使用了,
flag*=-1; //于是我们就用平方探查法来查找
key=(key%mod+mod)%mod; //防止出现负值
}
return key;
}
LL squ(int x)
{
return (LL) x*x;
}
void is_primer(int n)
{
for(int i=2;i<=sqrt(n);++i)
if(n%i==0)
{
cout << " not is primer ;\n";
return;
}
cout << "is primer\n";
return;
}
int main()
{
is_primer(test);
memset(hs,-1,sizeof(hs));
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
auto key=hash_key(x,y);
if(hs[key]==-1) //这一个if语句需不需要都行
hs[key]=hash_val(x,y);
if(!id[key]||r>id[key]) //如果id[key]第一次被使用,或者此点的半径比之前的大,
id[key]=r; //那么更新这个点的半径
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
dfs_Trave(x,y,r);
}
for(int i=0;i<n;++i)
{
auto key=hash_key(cir[i].x,cir[i].y);
if(vis[key]!=0)
++res;
}
printf("%d\n",res);
return 0;
}
void dfs(int x,int y,int r)
{
int key=hash_key(x,y);
vis[key]=1;
for(int l=x-r;l<=x+r;++l) //遍历(x,y)周围可以炸到的所有点
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
int key=hash_key(l,s);
if(hs[key]!=-1) //如果这个点处有炸弹
{
if(vis[key]==0) //如果这个点处的炸弹没被拆除掉
dfs(l,s,id[key]);
}
}
}
}
void dfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l) //遍历(x,y)周围可以炸到的所有点
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
int key=hash_key(l,s);
if(hs[key]!=-1) //如果这个点处有炸弹
{
if(vis[key]==0) //如果这个点处的炸弹没被拆除掉
dfs(l,s,id[key]);
}
}
}
}
第十一个, 用BFS实现图的遍历,
手写hash表:把每个点唯一表示一个值,然后存到一个数组中,由于最大值为1e9,
所以可以把x坐标乘以一个(1e9+1)+y的坐标表示一个long long 值,也不会溢出,
即表示为一个两位的进制数,不过这个进制是1e9+1;
true coding,能AC
值得一提的是,vis[key]应当在进入bfs的队列便更新这个值已被访问,否则取出一个坐标的时候再更新,会导致一个点多次入队,浪费许多时间,acwing上最后一组数据超时,问题便出现在这儿
其实算法笔记讲解BFS的时候就已经强调了inq表示结点是否入队,而不是是否访问,这和DFS的vis数组是有区别的,当是还不以为然,觉得自己都理解了,现在想想,亦是惭愧!书你倒是看了,但你是否真正的吸收了呢?每学到一个算法,就要去找相应的题目来做,不然你也只是白白浪费时间,多了不说,算法笔记上的树状数组以及lowbit数组你现在是否还能知道它们的意思,KMP算法是否还有印象,快速排序是否还能写出来,组合数的知识还知道多少。。。等等,不光是低头做题,还得总结自己学到的东西,以后遇到能够用自己学过的算法解决的题目的时候,别两眼一蹬,我不会?那就从此处开始,把之前写的算法发成博客吧,也能再温习一遍。
/**
用BFS实现图的遍历,
手写hash表:把每个点唯一表示一个值,然后存到一个数组中,由于最大值为1e9,
所以可以把x坐标乘以一个(1e9+1)+y的坐标表示一个long long 值,也不会溢出,
即表示为一个两位的进制数,不过这个进制是1e9+1;
true coding,能AC
*/
/**
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=1e9,mod=700001,ne=50010;
int test=700001; //测试数是否为素数
typedef long long LL;
struct Node
{
int x,y,r;
}cir[ne];
LL hs[mod]={0};
int id[mod]={0},vis[mod]={0};
int m,n;
void bfs(Node zd);
void bfs_Trave(int x,int y,int r);
LL hash_val(int x,int y) //将二维坐标转换为一个hash值
{
return (maxn+1ll)*x+y;
}
int hash_key(int x,int y)
{
LL val=hash_val(x,y);
int k=1,flag=-1;
int key=(val%mod+mod)%mod;
while(hs[key]!=-1&&hs[key]!=val) //此处需要hs[key]!=key,因为后面需要查找用到二维坐标,
{ //返回一个key值
key+=k*k*flag; //由于一个坐标最开始对应的key值也许被其他坐标占用了,这就需要查找
++k; //一个没被用到的值,但考虑到一个值一个值的加,元素容易扎堆都被使用了,
flag*=-1; //于是我们就用平方探查法来查找
key=(key%mod+mod)%mod; //防止出现负值
}
return key;
}
LL squ(int x)
{
return (LL) x*x;
}
void is_primer(int n)
{
for(int i=2;i<=sqrt(n);++i)
if(n%i==0)
{
cout << " not is primer ;\n";
return;
}
cout << "is primer\n";
return;
}
int main()
{
//is_primer(test);
memset(hs,-1,sizeof(hs));
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=0;i<n;++i)
{
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
auto key=hash_key(x,y);
if(hs[key]==-1) //这一个if语句需不需要都行
hs[key]=hash_val(x,y);
if(!id[key]||r>id[key]) //如果id[key]第一次被使用,或者此点的半径比之前的大,
id[key]=r; //那么更新这个点的半径
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
bfs_Trave(x,y,r);
}
for(int i=0;i<n;++i)
{
auto key=hash_key(cir[i].x,cir[i].y);
if(vis[key]!=0)
++res;
}
printf("%d\n",res);
return 0;
}
void bfs(Node zd)
{
queue<Node> q;
q.push(zd);
while(!q.empty())
{
Node temp=q.front();
int x=temp.x,y=temp.y,r=temp.r;
q.pop();
int key=hash_key(x,y);
// vis[key]=1;
for(int l=x-r;l<=x+r;++l) //遍历(x,y)周围可以炸到的所有点
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
int key=hash_key(l,s);
if(hs[key]!=-1) //如果这个点处有炸弹
{
if(vis[key]==0) //如果这个点处的炸弹没被拆除掉
{
q.push({l,s,id[key]});
vis[key]=1; //值得一提的是,vis[key]应当在进入bfs的队列便更新这个值已被访问
} //,否则取出一个坐标的时候再更新,会导致一个点多次入队
} //,浪费许多时间,acwing上最后一组数据超时,问题便出现在这儿
}
}
}
}
void bfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l) //遍历(x,y)周围可以炸到的所有点
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
int key=hash_key(l,s);
if(hs[key]!=-1) //如果这个点处有炸弹
{
if(vis[key]==0) //如果这个点处的炸弹没被拆除掉
{
vis[key]=1;
bfs({l,s,id[key]});
}
}
}
}
}
*/最后一个代码,是acwing上看的,因为我写的BFS始终由一组数据通不过,便对照着他的写,但还是有一组数据通不过,根本原因还是BFS入队的时候便要更新坐标已入队,否则会造成一个点多次入队,这一点必须谨记。和上一个一个代码唯一的不同便是这个id数组记录的是cir数组的下标,也就是存储在cir数组里的下标,上一个id存储的相同点的最大半径。
/**借鉴正确代码
*/
/**
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <cmath>
#include <cstring>
using namespace std;
const int maxn=1e9,mod=1e6 + 7,ne=50010;
int test=700001; //测试数是否为素数
typedef long long LL;
struct Node
{
int x,y,r;
}cir[ne];
LL hs[mod]={0};
int id[mod]={0}; //id存储的是坐标在数组cir中对应的下标
bool vis[ne]={0};
int m,n;
void bfs(int index);
void bfs_Trave(int x,int y,int r);
LL hash_val(int x,int y) //将二维坐标转换为一个hash值
{
return (maxn+1ll)*x+y;
}
int hash_key(int x,int y)
{
LL val=hash_val(x,y);
int key=(val%mod+mod)%mod;
while(hs[key]!=-1&&hs[key]!=val) //此处需要hs[key]!=key,因为后面需要查找用到二维坐标,
{ //返回一个key值
key++;
if(key == mod) key = 0; //防止出现负值
}
return key;
}
LL squ(int x)
{
return (LL) x*x;
}
int main()
{
memset(hs,-1,sizeof(hs));
scanf("%d%d",&n,&m);
int x,y,r;
for(int i=1;i<=n;++i)
{
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
auto key=hash_key(x,y);
if(hs[key]==-1) //这一个if语句需不需要都行
hs[key]=hash_val(x,y);
if(!id[key]||r>cir[id[key]].r) //如果id[key]第一次被使用,或者此点的半径比之前的大,
id[key]=i; //那么更新这个点的坐标下标
}
int res=0;
for(int i=0;i<m;++i)
{
scanf("%d%d%d",&x,&y,&r);
bfs_Trave(x,y,r);
}
for(int i=1;i<=n;++i)
{
auto key=hash_key(cir[i].x,cir[i].y);
int pos=id[key];
if(pos&&vis[pos])
++res;
}
printf("%d\n",res);
return 0;
}
void bfs(int index)
{
queue<int> q;
q.push(index);
vis[index]=1;
while(!q.empty())
{
int temp=q.front();
int x=cir[temp].x,y=cir[temp].y,r=cir[temp].r;
q.pop();
//int key=hash_key(x,y);
//vis[temp]=1; //在这儿将temp号的值赋为1便是错的,不知道原因
for(int l=x-r;l<=x+r;++l) //遍历(x,y)周围可以炸到的所有点
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
int key=hash_key(l,s);
if(id[key]&&!vis[id[key]]) //如果这个点处有炸弹
{
int pos=id[key];//如果这个点处的炸弹没被拆除掉
q.push(pos);
vis[pos]=1;
}
}
}
}
}
void bfs_Trave(int x,int y,int r)
{
for(int l=x-r;l<=x+r;++l) //遍历(x,y)周围可以炸到的所有点
for(int s=y+r;s>=y-r;--s)
{
if(squ(r) >= squ(l-x) + squ(s-y))
{
int key=hash_key(l,s);
if(id[key]&&!vis[id[key]]) //如果这个点处有炸弹
{ //如果这个点处的炸弹没被拆除掉
bfs(id[key]);
}
}
}
}边栏推荐
- leetcode 统计无向图中无法互相到达点对数
- Matrix eigenvalue and eigenvector solution - eigenvalue decomposition (EVD)
- PHP database ODBC
- PWN attack and defense world level2
- Leetcode counts the logarithm of points that cannot reach each other in an undirected graph
- PWN攻防世界guess_num
- Ctfhub web password weak password
- PHP XML expat parser
- String segment combination
- 均贫富
猜你喜欢
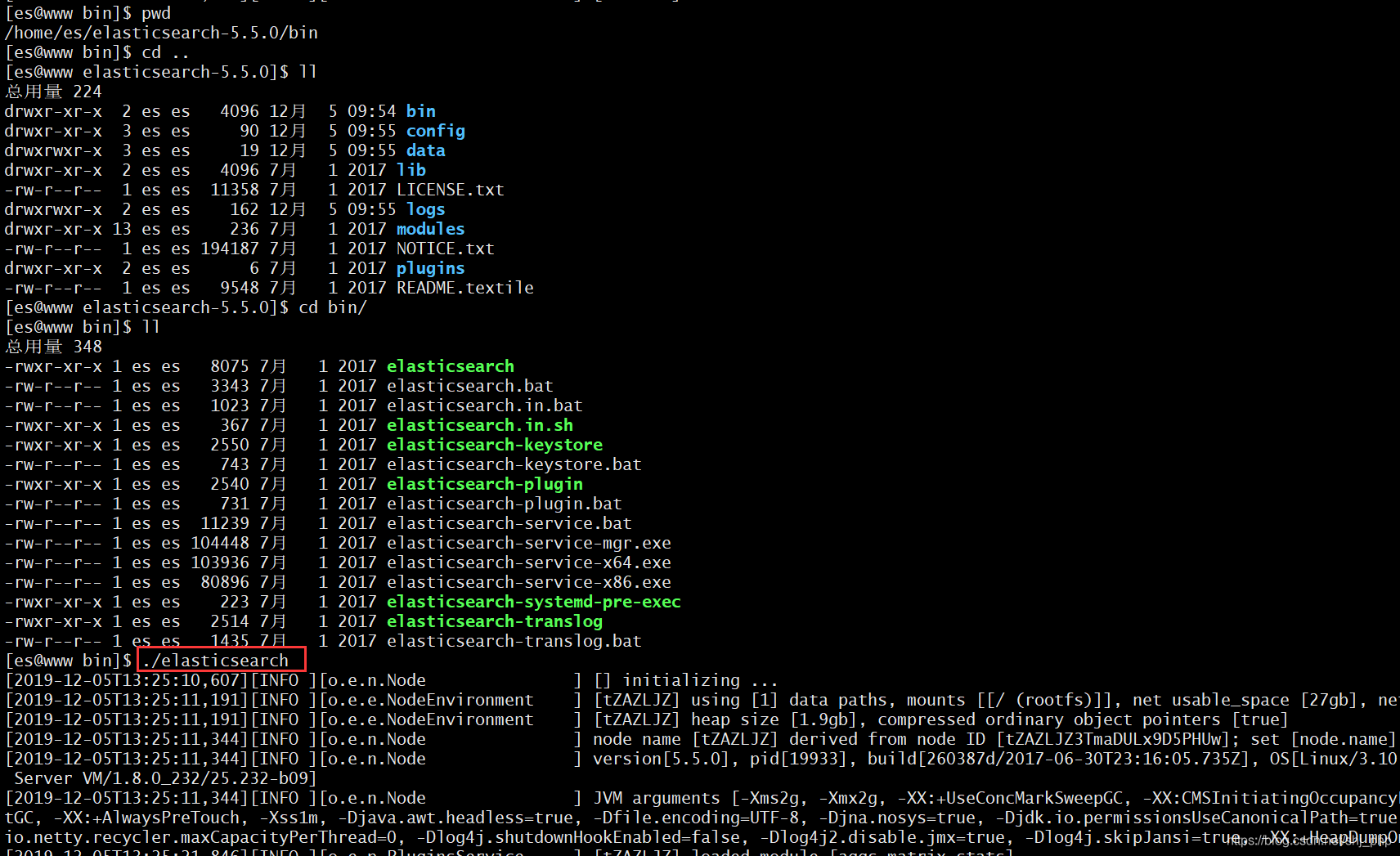
Install kibana

1110: 最近共同祖先(函数专题)
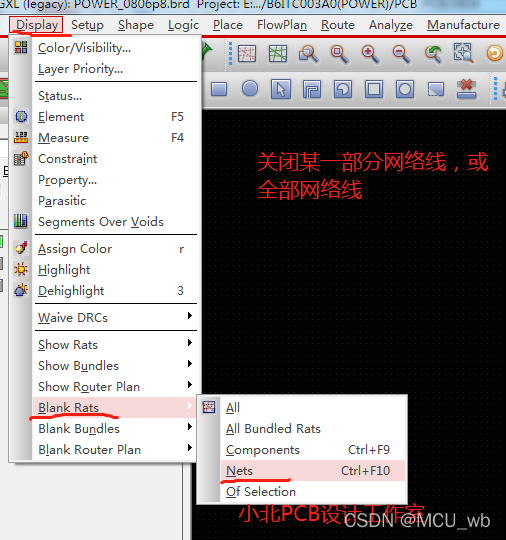
allegro 设计中显示网络飞线或关闭网络飞线的方法

What is Mipi
![[linear algebra] 1.1 second and third order determinants](/img/ea/70b59c64d3287a887e371a9181fe45.png)
[linear algebra] 1.1 second and third order determinants

allegro对走好的线取消走线的方法
If you dare to write MQ message queue middleware on your resume, you must win these questions!

18. `bs对象.节点名.next_sibling` 获取兄弟节点

双击事件与单击事件的那些事

Oracle Recovery Tools实战批量坏块修复
随机推荐
Wechat applet custom component
手机开户股票开户安全吗?开户很难么?
fsockopen函数的应用
Download and installation of MySQL
String method exercise
If you dare to write MQ message queue middleware on your resume, you must win these questions!
解决allegro中测量距离时,点击一个点后光标闪烁的问题
线程池是什么老鸡?
月薪没到30K的程序员必须要背的面试八股,我先啃为敬
均贫富
SQL training 01
18. `bs对象.节点名.next_sibling` 获取兄弟节点
Ctfhub web password default password
层次分析法(AHP)
[issue 259] uncover how count is executed in MySQL?
Tuples of combined data types
What is a thread pool?
SQL continuous login problem
Use photoshop2022 to create a wonderful gradient effect for pictures
Tortoise 没有显示绿色图标