DSP Trick：向量长度估算

最近看Richard G. Lyons的Understanding Digital Signal Processing 时学到的向量长度估算技巧，Alpha-max-plus-beta-min algorithm，还挺好用。

Motivation

考虑在[0,pi/2]区间中的一段以原点为圆心半径为1的弧，由圆心指向弧上任一点(x,y)的向量，长度为1。把x、y和向量长度的图像画出来是这样的：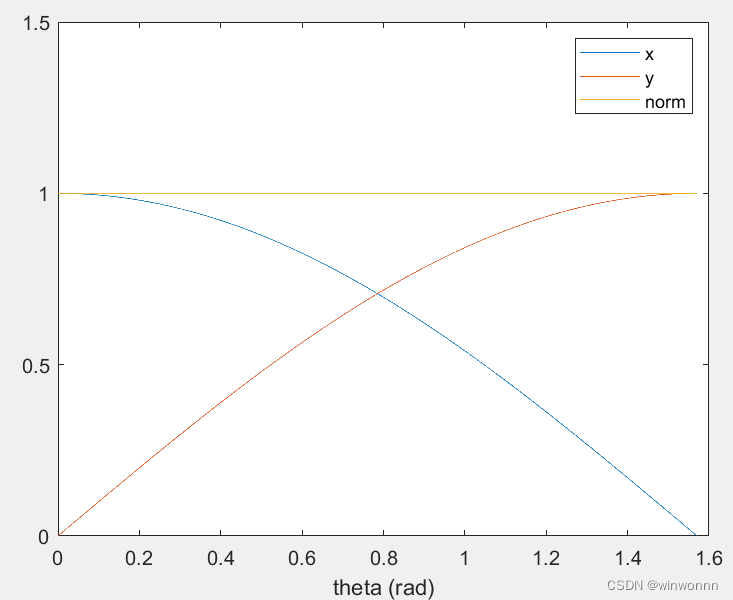
这张图给人一种直觉，是不是可以取max(x,y)来近似向量长度呢？这样做的话在0和pi/2的时候都是ok的，最大误差出现在pi/4的时候，max(x,y)约为0.707，误差30%；进一步思考，在0和pi/2的时候，min(x,y)都是0，那么如果加上一定比例的min(x,y)，是不是能够得到更好的近似效果呢？
也就是——
$$estimation=\alpha \ast max(x,y)+\beta \ast min(x,y)$$

理论推导

以下内容主要参考 Smyk R , M Czyżak. Improved magnitude estimation of complex numbers using alpha max and beta min algorithm. 2016.

方便起见，考虑[0,pi/4]区间的情况即可，其他区间的向量都可以转换到这里。

所以，现在的问题是，如何取合适的$\alpha$和$\beta$？
首先，近似误差公式可以写出来
$$e(\theta )=1-\alpha cos(\theta )-\beta sin(\theta )$$

下面是来自论文的推导——注意式(9a)的符号有点错误

最终论文给出了一个结果列表供参考——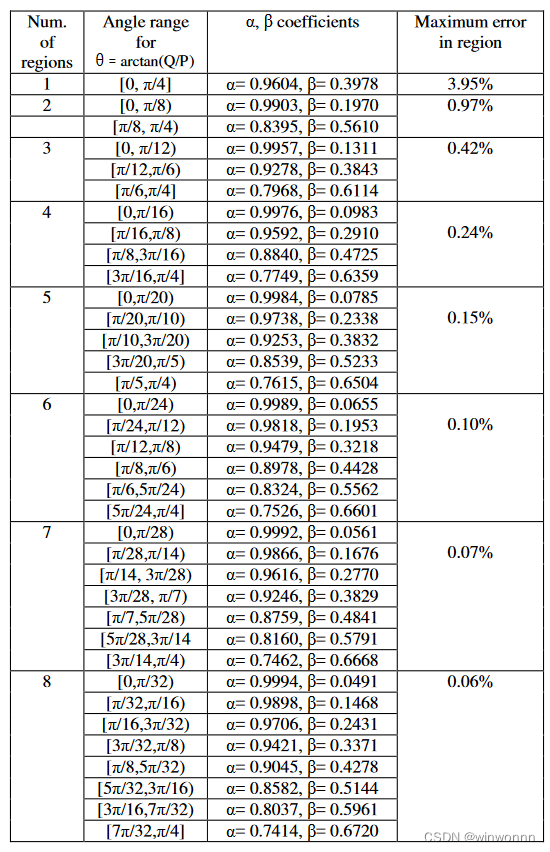

Code

取了3 regions的一个定点运算的程序，放在了My Github