当前位置:网站首页>n皇后问题(回溯法)
n皇后问题(回溯法)
2022-08-02 03:28:00 【Aiolei】
1. 问题
在有 n*n 方格的棋盘中放置 n 个皇后,使得任何两个皇后之间不能相互攻击,即在同一行同一列不能有两个以上的皇后,在与主对角线、副对角线的平行线上也不能有两个以上的皇后,试给出所有的放置方法。
2. 分析
n 皇后问题是回溯法中的经典问题
我们可以选择逐行放皇后,先给第一行放皇后,很显然我们会把它放在第一列。接下来,给第二行放皇后,那么第二行的皇后能放在哪些位置呢?这时候需要一个判断函数 judge() 来判断第二列的皇后能放在哪里。
判断的条件就是:该行的皇后与前面已放置好的皇后的列数不能相同,并且还不能在同一主副对角线上。这里使用了数组 pos[] 来记录列数,即 row 表示行数, pos[row] 表示当前该行的列数。同列好判断,即i循环列数,只要不要 p o s [ i ] = = p o s [ r o w ] pos[i]==pos[row] pos[i]==pos[row] 即可;对角线判断可以使用绝对值,如果行数相减的绝对值等于列数相减的绝对值 a b s ( r o w − i ) = = a b s ( p o s [ r o w ] − p o s [ i ] ) abs(row-i)==abs(pos[row]-pos[i]) abs(row−i)==abs(pos[row]−pos[i]),那么两个皇后就在同一对角线上,不满足。
如果第二行找到放皇后的某一列,那么就进行第三行的摆放…
在放置皇后过程中,如果该行的所有列均不可放皇后,那么便回溯到上一行,重新选择放置皇后的位置,再进行下一行的操作。
3. 代码
#include<iostream>
#include<cmath>
#include<cstdlib>
using namespace std;
int n, sum = 0; //皇后数量n
int pos[20]; //记录每个皇后应该放置的列数
//判断该位置能否放皇后
bool judge(int row)
{
for(int i = 1;i < row;i++){
//同列或同对角线上不能放皇后
if((pos[i]==pos[row]) || (abs(row-i)==abs(pos[row]-pos[i])))
return false;
}
//cout<<"行:"<<row<<",列:" <<pos[row]<<endl; //用于调试
return true;
}
//回溯法
void backtrack(int row)
{
if(row > n) //说明行数超出棋盘大小,已排好一次
sum++;
else{
for(int i = 1;i <= n;i++){
pos[row] = i; //目前是第row行第i列
if(judge(row)){
//能放置皇后则进入下一行
backtrack(row+1);
}
}
}
}
int main()
{
cout<<"输入皇后的数量 n = ";
cin>>n;
backtrack(1);
cout<<n<<"皇后有"<<sum<<"种解法!"<<endl;
return 0;
}
4. 效果
4皇后
8皇后
边栏推荐
猜你喜欢
十大实用的办公工具网站,可以解决你日常100%的问题

成本会计的概念、产品成本核算的要求、产品成本核算的对象与成本项目、产品成本的归集和分配(可能考判断)、产品成本计算方法 (三种:产品的品种(品种法),批次(分批法),步骤(分步法))

分布式消息队列平滑迁移技术实战

Microsoft Office安装全过程记录
元宇宙:为何互联网大佬纷纷涉足?元宇宙跟NFT是什么关系?

关于我的专利、软著~
库存现金、现金管理制度、现金的账务处理、银行存款、银行存款的账务处理、银行存款的核对
Debian 12 Bookworm 尝鲜记

【opencv】error: (-215:Assertion failed) ssize.empty() in function ‘cv::resize‘报错原因
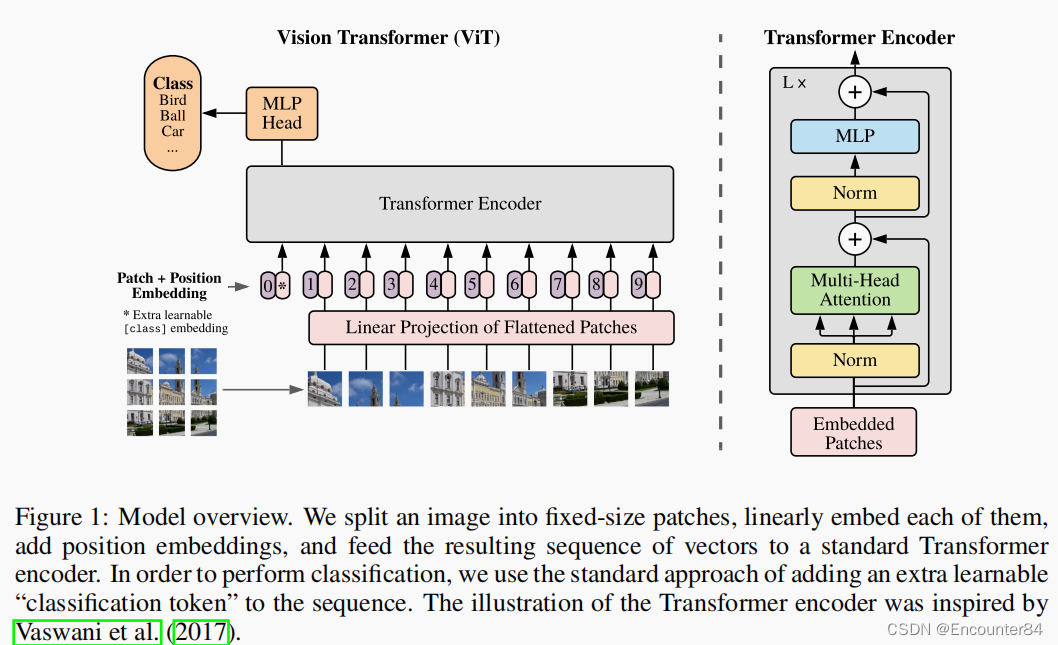
Vision Transformer(ViT)论文精读和Pytorch实现代码解析
随机推荐
3D建模作品
大厂底层必修:“应用程序与 AMS 的通讯实现”
分布式消息队列平滑迁移技术实战
Visual Studio2022创建setup项目
ReentrantLock的使用和原理详解
中国大陆开源镜像站汇总
Out of memory error on GPU 0. Cannot allocate xxxGB memory on GPU 0, available memory is only xxx
PHP hash加密与解密
Laravel 验证唯一时排除修改时的数据
聊聊MySQL的10大经典错误
深度学习理论:测试集与验证集的区别及各自用途
关于我的数学建模~
同时安装VirtualBox和VMware,虚拟机如何上网
关于我的项目-微信小程序2(uniapp->wx小程序)
Kotlin - 标准函数(with、run和apply)
php中魔术方法详解
Acwing:哈夫曼树(详解)
Dcat Admin 关闭代码生成器 登录指定地址
C# 常用方法记录
Larave 自定义公共函数以及引入使用