Detailed explanation and code example of affinity propagation clustering calculation formula based on graph

Spectral clustering and AP Clustering is two kinds of clustering based on graph , Here I introduce AP clustering .

Affinity Propagation Clustering（ abbreviation AP Algorithm ） yes 2007 Proposed , It was published in Science On 《single-exemplar-based》. Especially suitable for high dimension 、 Fast clustering of multi class data , Compared with the traditional clustering algorithm , The algorithm is relatively new , Clustering performance and efficiency have been greatly improved .

Affinity Propagation It can be translated into relevance communication , It is based on data points “ The messaging ” Clustering technology of concepts , So we call it graph based clustering .

The algorithm creates clusters by sending messages between data points until convergence . It takes the similarity between data points as input , And determine examples according to certain standards . Exchange messages between data points , Until you get a set of high-quality examples . And k-means or k-medoids And other clustering algorithms are different , Propagation does not need to determine or estimate the number of clusters before running the algorithm .

Detailed explanation of the formula

We use the following data set , To introduce the working principle of the algorithm .

Similarity matrix

Each cell in the similarity matrix is calculated by negating the sum of squares of differences between participants .

such as Alice and Bob The similarity , The sum of the squares of the differences is (3–4)² + (4–3)² + (3–5)² + (2–1)² + (1– 1)² = 7. therefore ,Alice and Bob The similarity value of is -(7).

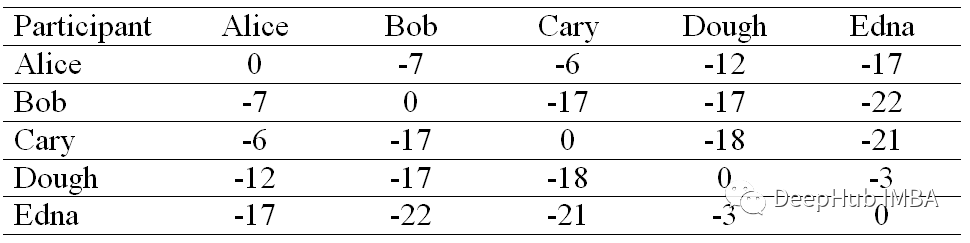
If you choose a smaller value for the diagonal , Then the algorithm will converge around a small number of clusters , vice versa . So we use -22 Fill the diagonal elements of similar matrices , This is the minimum value in our similarity matrix .

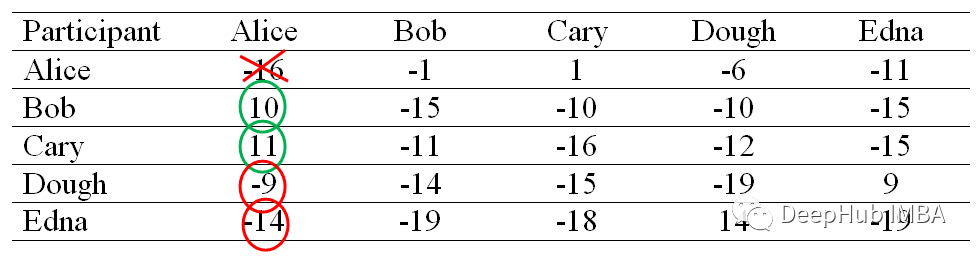
Attractiveness （Responsibility） matrix

We will first construct a structure where all elements are set to 0 Availability matrix . then , We will use the following formula to calculate each cell in the attractiveness matrix :

here i It means line ,k It refers to the column of the correlation matrix .

for example ,Bob( Column ) Yes Alice( That's ok ) The degree of attraction is -1, This is done through Bob and Alice The similarity (-7) Subtract from Alice The maximum similarity of the line (Bob and Alice The similarity (-6) With the exception of ) Calculated .

After calculating the attractiveness of other participants , We get the following matrix .

Attractiveness is used to describe points k Suitable for data points i The degree of clustering center .

Attribution degree （Availability） matrix

In order to construct a attribution matrix , Two separate equations of diagonal and off diagonal elements will be used for calculation , And apply them to our attractiveness matrix .

Diagonal elements will use the following formula .

here i It refers to the row sum of the incidence matrix k Column .

This equation tells us to calculate all values greater than... Along the column 0 The sum of the values of , Except for rows with values equal to the columns in question . for example ,Alice The element value on the diagonal of will be Alice The sum of the positive values of the columns , But does not include Alice The value of the column , be equal to 21(10 + 11 + 0 + 0).

After modification , Our attribution matrix will be as follows ：

Now for off diagonal elements , Update their values using the following equation .

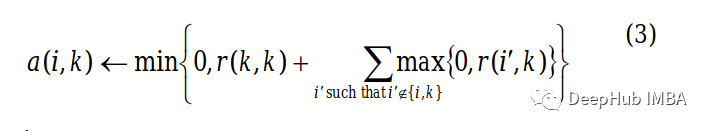
Understand the above equation through an example . Suppose we need to find Bob（ Column ） Yes Alice（ That's ok ） The degree of belonging , Then it will be Bob My self belonging （ On the diagonal ） and Bob The sum of the remaining positive attractiveness of the column , barring Bob Of Alice That's ok （-15 + 0 + 0 + 0 = -15）.

After calculating the rest , Get the following attribution matrix .

Belonging degree can be understood as describing points i Select point k The suitability as its clustering center .

Applicable （Criterion） matrix

Each cell in the applicable matrix is only the sum of the attraction matrix and the attribution matrix of the position .

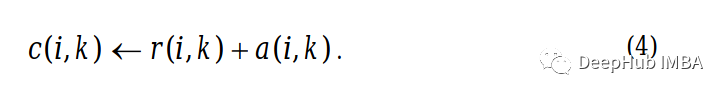
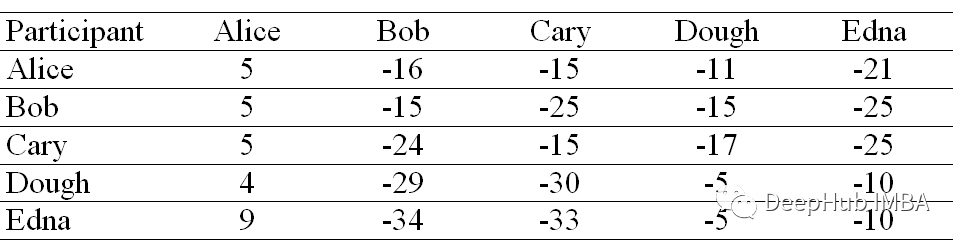
The column with the highest applicable value in each row is designated as the sample . Rows sharing the same instance are in the same cluster . In our example .Alice、Bob、Cary 、Doug and Edna All belong to the same cluster .

If this is the case ：

that Alice、Bob and Cary Form a cluster , and Doug and Edna Form the second cluster .

Criterion Translated by me, it means that this matrix is the criterion and basis for our clustering algorithm .

Code example

stay sklearn The algorithm has been included in , So we can use it directly ：

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation

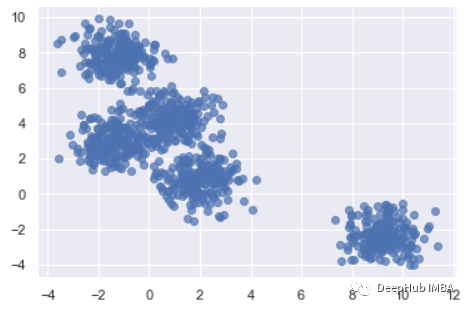
from Sklearn Generate clustering data

X, clusters = make_blobs(n_samples=1000, centers=5, cluster_std=0.8, random_state=0)
plt.scatter(X[:,0], X[:,1], alpha=0.7, edgecolors='b')

Initialize and fit the model .

af = AffinityPropagation(preference=-50)
clustering = af.fit(X)

AP In clustering applications, you need to manually specify Preference and Damping factor, Although there is no need to explicitly specify the number of clusters , But these two parameters are actually the original clustering “ Number ” Controlled variants ：

Preference： The data points i The reference degree of is called p(i) or s(i,i), It's about pointing i As the reference of cluster center , The number of clusters is subject to reference p Influence , If you think that every data point can be used as a cluster center , that p You should take the same value . If the average of the input similarity is taken as p Value , The number of clusters is medium . If the minimum value is taken , Get clusters with fewer classes .

Damping factor( Damping coefficient )： Mainly for convergence .

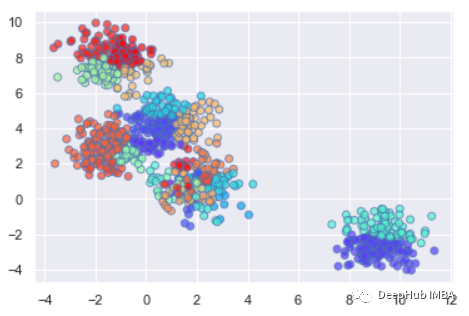
Draw data points of clustering results

plt.scatter(X[:,0], X[:,1], c=clustering.labels_, cmap=‘rainbow’, alpha=0.7, edgecolors=‘b’)

summary

Affinity Propagation It's an unsupervised machine learning technology , It is especially applicable when we do not know the optimal number of clusters . And the algorithm has high complexity , So the running time is compared K-Means A lot longer , This will make it a lot of time, especially when running under massive data .

https://avoid.overfit.cn/post/70c0efd697ef43a6a43fea8938afff60

author ：Sarthak Kedia