当前位置:网站首页>Personalized federated learning using hypernetworks paper reading notes + code interpretation
Personalized federated learning using hypernetworks paper reading notes + code interpretation
2022-06-12 07:17:00 【Programmer long】
The address of the paper is here
One . Introduce
Federated learning is the task of learning models on multiple disjoint local data sets , Because of privacy 、 Unable to share local datasets due to storage problems . But when the data is distributed among different clients , Learning a single global model may fail . To handle this cross client heterogeneity , Personalized federated learning enables each client to adjust itself .
pFedHN Use hypernetwork (Hypernetwork) To generate shadow network parameters for each input . Each client has a unique embedded vector , This vector is passed as input to the hypernetwork , So most book parameters are shared between clients .
Another benefit of using a hypernetwork is , The training parameter vector of the super network will never be transmitted , Each client only needs to accept its own network parameters for prediction and gradient calculation , Hypernetworks only need to accept gradients to optimize their own parameters .
Two . Related work
Federal learning : For data privacy 、 Communication problems, etc , Each client cannot transmit data , Only parameters can be transmitted . Federal learning to FedAvg The most famous , But then all clients will learn a global model , And can not meet the personalized .
Federal personalized learning : Federated learning settings present many challenges , Including data heterogeneity , Heterogeneous devices . In particular, data heterogeneity makes it very difficult to learn a shared global model for all clients . There are many ways , For example, based on MAML Meta learning and personalized learning , The personalization layer implements .
Hypernetwork : Hypernetwork by Klein Deep neural network proposed by et al , Its output is the weight of another target network of the learning task . The idea is that the output weight changes with the input of the super network .
3、 ... and . Method
3.1 Federal personalization questions indicate
For a personalized federal learning , Each client has its own parameters θ i \theta_i θi, Data set distribution P i \mathcal{P}_i Pi Corresponding m Data examples S i = { ( x j ( i ) , y j ( i ) ) } i = 1 m i \mathcal{S_i}=\{(x_j^{(i)},y_j^{(i)})\}_{i=1}^{m_i} Si={ (xj(i),yj(i))}i=1mi, So we use L i ( θ i ) = 1 m i ∑ j l i ( x i , y i ; θ i ) \mathcal{L}_i(\theta_i) = \frac{1}{m_i}\sum_jl_i(x_i,y_i;\theta_i) Li(θi)=mi1∑jli(xi,yi;θi), To represent the loss of a client , Then the optimization goal of our federal personalized learning is :
Θ ∗ = a r g min Θ 1 n ∑ i = 1 n E x , y ~ P i [ l i ( x j , y j ; θ i ) ] \Theta^*=arg\min_{\Theta}\frac{1}{n}\sum_{i=1}^n \mathbb{E}_{x,y~\mathcal{P_i}}[l_i(x_j,y_j;\theta_i)] Θ∗=argΘminn1i=1∑nEx,y~Pi[li(xj,yj;θi)]
For training, the optimization goal is :
a r g min θ 1 n ∑ i = 1 n L i ( θ i ) = a r g min θ 1 n ∑ i = 1 n 1 m i ∑ j = 1 m i [ l i ( x j , y j ; θ i ) ] arg \min_{\theta}\frac{1}{n}\sum_{i=1}^n\mathcal{L}_i(\theta_i)=arg \min_{\theta}\frac{1}{n}\sum_{i=1}^n\frac{1}{m_i}\sum_{j=1}^{m_i}[l_i(x_j,y_j;\theta_i)] argθminn1i=1∑nLi(θi)=argθminn1i=1∑nmi1j=1∑mi[li(xj,yj;θi)]
3.2 Federal hypernetwork
The hypernetwork outputs the weight of another network according to its input . We use h ( . ; φ ) h(.;\varphi) h(.;φ) Represents our hypernetwork . With f ( . ; θ ) f(.;\theta) f(.;θ) Represents our target network ( That is, classified networks ). Hypernetwork is deployed on the server , Each client embeds vectors by passing them to the server v To get the corresponding parameters , After training, set the parameters of your own network θ \theta θ Of The gradient is returned to the server , The specific picture is as follows :
Therefore, we change our corresponding optimization objectives to :
a r g min φ , v 1 , . . . . v n 1 n ∑ i = 1 n L i ( h ( v i ; φ ) ) arg \min_{\varphi,v_1,....v_n}\frac{1}{n}\sum_{i=1}^n\mathcal{L}_i(h(v_i;\varphi)) argφ,v1,....vnminn1i=1∑nLi(h(vi;φ))
By using the chain rule, we can calculate ∇ φ L i = ( ∇ φ θ i ) T ∇ θ i L i \nabla_{\varphi}\mathcal{L}_i = (\nabla_{\varphi}\theta_i)^T\nabla_{\theta_i}\mathcal{L_i} ∇φLi=(∇φθi)T∇θiLi, So we just need to compute on the client side θ \theta θ The gradient of is returned to the server .
The author here uses a more general rule to update , By using Δ θ i = θ i ~ − θ \Delta \theta_i = \widetilde{\theta_i}-\theta Δθi=θi−θ Replace θ \theta θ Gradient of ( here θ i ~ \widetilde{\theta_i} θi Corresponding to the training on the client k individual epoch Post update results ).
The training process is shown in the figure below :
Finally, the author also said , When using the super network, we should only use the weight output of the feature layer for each client target network , Avoid problems such as irrelevance between client tasks .
Four . Key code interpretation
The author's github Code point here , We will explain the above process .
The first is construction hypernetwork and target network
about hypernetwork, We accept vectors from each client v, Generate target network Corresponding weight , as follows :
class CNNHyperPC(nn.Module):
def __init__(
self, n_nodes, embedding_dim, in_channels=3, out_dim=10, n_kernels=16, hidden_dim=100,
spec_norm=False, n_hidden=1):
super().__init__()
self.in_channels = in_channels
self.out_dim = out_dim
self.n_kernels = n_kernels
self.embeddings = nn.Embedding(num_embeddings=n_nodes, embedding_dim=embedding_dim)
layers = [
spectral_norm(nn.Linear(embedding_dim, hidden_dim)) if spec_norm else nn.Linear(embedding_dim, hidden_dim),
]
for _ in range(n_hidden):
layers.append(nn.ReLU(inplace=True))
layers.append(
spectral_norm(nn.Linear(hidden_dim, hidden_dim)) if spec_norm else nn.Linear(hidden_dim, hidden_dim),
)
self.mlp = nn.Sequential(*layers)
self.c1_weights = nn.Linear(hidden_dim, self.n_kernels * self.in_channels * 5 * 5)
self.c1_bias = nn.Linear(hidden_dim, self.n_kernels)
self.c2_weights = nn.Linear(hidden_dim, 2 * self.n_kernels * self.n_kernels * 5 * 5)
self.c2_bias = nn.Linear(hidden_dim, 2 * self.n_kernels)
self.l1_weights = nn.Linear(hidden_dim, 120 * 2 * self.n_kernels * 5 * 5)
self.l1_bias = nn.Linear(hidden_dim, 120)
self.l2_weights = nn.Linear(hidden_dim, 84 * 120)
self.l2_bias = nn.Linear(hidden_dim, 84)
if spec_norm:
self.c1_weights = spectral_norm(self.c1_weights)
self.c1_bias = spectral_norm(self.c1_bias)
self.c2_weights = spectral_norm(self.c2_weights)
self.c2_bias = spectral_norm(self.c2_bias)
self.l1_weights = spectral_norm(self.l1_weights)
self.l1_bias = spectral_norm(self.l1_bias)
self.l2_weights = spectral_norm(self.l2_weights)
self.l2_bias = spectral_norm(self.l2_bias)
def forward(self, idx):
emd = self.embeddings(idx)
features = self.mlp(emd)
weights = {
"conv1.weight": self.c1_weights(features).view(self.n_kernels, self.in_channels, 5, 5),
"conv1.bias": self.c1_bias(features).view(-1),
"conv2.weight": self.c2_weights(features).view(2 * self.n_kernels, self.n_kernels, 5, 5),
"conv2.bias": self.c2_bias(features).view(-1),
"fc1.weight": self.l1_weights(features).view(120, 2 * self.n_kernels * 5 * 5),
"fc1.bias": self.l1_bias(features).view(-1),
"fc2.weight": self.l2_weights(features).view(84, 120),
"fc2.bias": self.l2_bias(features).view(-1),
}
return weights
First pass through nn.Embedding layer , This layer is mainly used for vector coding ( You can search for details , That is to encode each word vector ), After that, it passes through the base course Linear Hidden layer ( Here the author writes spectral_norm Corresponding to spectral normalization , But it is not used in training , Should be a better fit ), After all this, we target The parameters of each layer of the corresponding weight and bias For the output .
Next, the corresponding feature extraction part of the target model , It corresponds to the parameters of the above output one by one
class CNNTargetPC(nn.Module):
def __init__(self, in_channels=3, n_kernels=16):
super().__init__()
self.conv1 = nn.Conv2d(in_channels, n_kernels, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(n_kernels, 2 * n_kernels, 5)
self.fc1 = nn.Linear(2 * n_kernels * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return x
Finally, there is an output layer , This layer comes with each model , Not participating in hypernetwork
class LocalLayer(nn.Module):
def __init__(self, n_input=84, n_output=2, nonlinearity=False):
super().__init__()
self.nonlinearity = nonlinearity
layers = []
if nonlinearity:
layers.append(nn.ReLU())
layers.append(nn.Linear(n_input, n_output))
self.layer = nn.Sequential(*layers)
def forward(self, x):
return self.layer(x)
Once the network is defined, you can start training
First, each client generates its own identifier and sends it to hypernetwork Get parameters . It's very simple , The label generated by each client is the identifier ( for example 1 No. client is selected for training , Then in tensor[1] To hypernetwork)
node_id = random.choice(range(num_nodes))
# produce & load local network weights
weights = hnet(torch.tensor([node_id], dtype=torch.long).to(device))
net.load_state_dict(weights)
After that, the client will train and update its own parameters
(clip_grad_norm_ For trimming gradient , Prevent gradient explosions )
for i in range(inner_steps):
net.train()
inner_optim.zero_grad()
optimizer.zero_grad()
nodes.local_optimizers[node_id].zero_grad()
batch = next(iter(nodes.train_loaders[node_id]))
img, label = tuple(t.to(device) for t in batch)
net_out = net(img)
pred = nodes.local_layers[node_id](net_out)
loss = criteria(pred, label)
loss.backward()
torch.nn.utils.clip_grad_norm_(net.parameters(), 50)
inner_optim.step()
nodes.local_optimizers[node_id].step()
At this time, let's update the parameter gradient of the hypernetwork
Δ θ i = θ i ~ − θ \Delta \theta_i = \widetilde{\theta_i}-\theta Δθi=θi−θ As an update to the target network
Used here torch,autograd.grad, This function calculates the gradient , Because our output is a vector, not a scalar , therefore grad_outputs Not for None, And the corresponding here is Δ θ i = θ i ~ − θ \Delta \theta_i = \widetilde{\theta_i}-\theta Δθi=θi−θ.
final_state = net.state_dict()
delta_theta = OrderedDict({
k: inner_state[k] - final_state[k] for k in weights.keys()})
# calculating phi gradient
hnet_grads = torch.autograd.grad(
list(weights.values()), hnet.parameters(), grad_outputs=list(delta_theta.values())
)
# update hnet weights
for p, g in zip(hnet.parameters(), hnet_grads):
p.grad = g
torch.nn.utils.clip_grad_norm_(hnet.parameters(), 50)
optimizer.step()
This is the end of the training process , It's not complicated on the whole , Of course, corresponding to the above algorithm discovery v I haven't changed , In fact, it has changed , there v The actual corresponding identifier is input to hypernetwork One of the first Embedding The resulting value , and Embedding As a parameter, it is naturally updated .
边栏推荐
- knife4j 初次使用
- Why must coordinate transformations consist of publishers / subscribers of coordinate transformation information?
- Map to sort
- Esp8266 firmware upgrade method (esp8266-01s module)
- paddlepaddl 28 支持任意维度数据的梯度平衡机制GHM Loss的实现(支持ignore_index、class_weight,支持反向传播训练,支持多分类)
- lambda 函数完美使用指南
- Category 7
- Embedded gd32 code read protection
- Expansion of D @nogc
- Junior high school education, less than 3k, to 30k+ monthly salary, how wonderful life is without restrictions
猜你喜欢
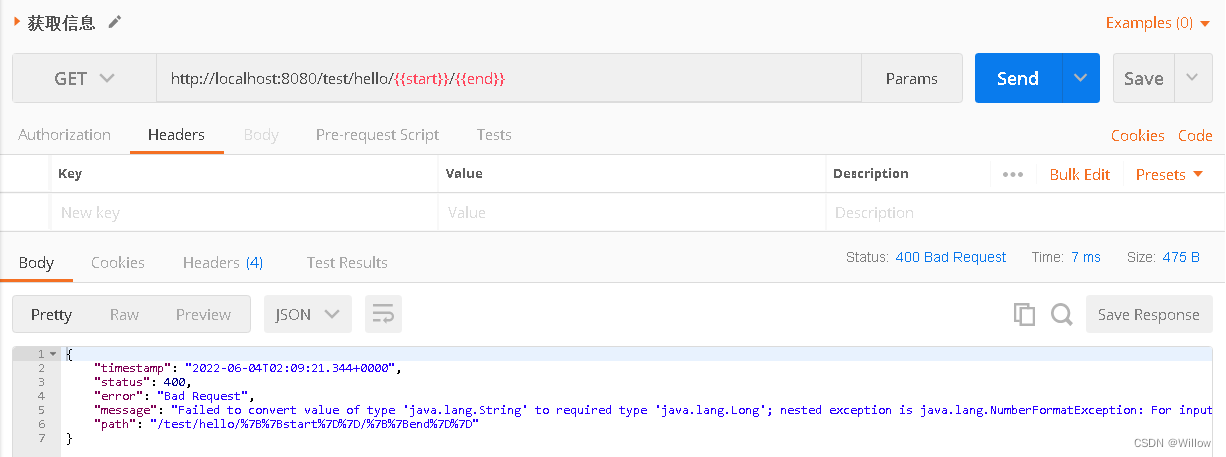
postman拼接替换参数循环调用接口
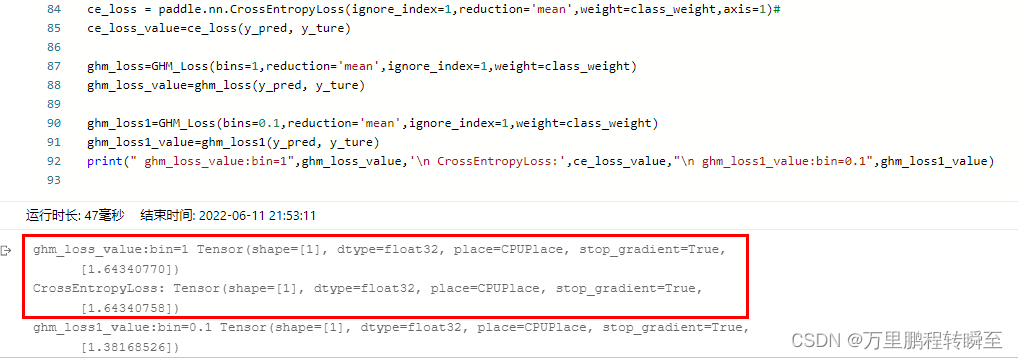
Paddepaddl 28 supports the implementation of GHM loss, a gradient balancing mechanism for arbitrary dimensional data (supports ignore\u index, class\u weight, back propagation training, and multi clas

Pyhon的第六天

Study on display principle of seven segment digital tube

Jackson XML is directly converted to JSON without writing entity classes manually

Postman splice replacement parameter loop call interface

Principle and application of PWM

leetcode. 39 --- combined sum
最近面了15个人,发现这个测试基础题都答不上来...

SQL Server 2019 installation error. How to solve it
随机推荐
Go common usage
paddlepaddl 28 支持任意维度数据的梯度平衡机制GHM Loss的实现(支持ignore_index、class_weight,支持反向传播训练,支持多分类)
公众号也能带货?
Summary from November 29 to December 5
Android studio uses database to realize login and registration interface function
Esp8266 firmware upgrade method (esp8266-01s module)
"I was laid off by a big factory"
Detailed explanation of addressing mode in 8086
Beginners can't tell the difference between framework and class library
Freshmen are worried about whether to get a low salary of more than 10000 yuan from Huawei or a high salary of more than 20000 yuan from the Internet
The most understandable explanation of coordinate transformation (push to + diagram)
Interview intelligence questions
Unity用Shader实现UGU i图片边缘选中高亮
LVDS drive adapter
sql server 2019安装出现错误,如何解决
Difference and application of SPI, UART and I2C communication
推荐17个提升开发效率的“轮子”
ROS dynamic parameter configuration: use of dynparam command line tool (example + code)
Detailed principle of 4.3-inch TFTLCD based on warship V3
[image denoising] image denoising based on nonlocal Euclidean median (nlem) with matlab code