动态规划之线性dp(上)

一、 三角形最小路径和

给定一个正三角形数组，自顶到底分别有 1，2，3，4，5…，n 个元素，找出自顶向下的最小路径和。

每一步只能移动到下一行的相邻节点上，相邻节点指下行种下标与之相同或下标加一的两个节点。

数据范围：三角形数组行数满足 1≤n≤200 ，数组中的值都满足 ∣val∣≤10^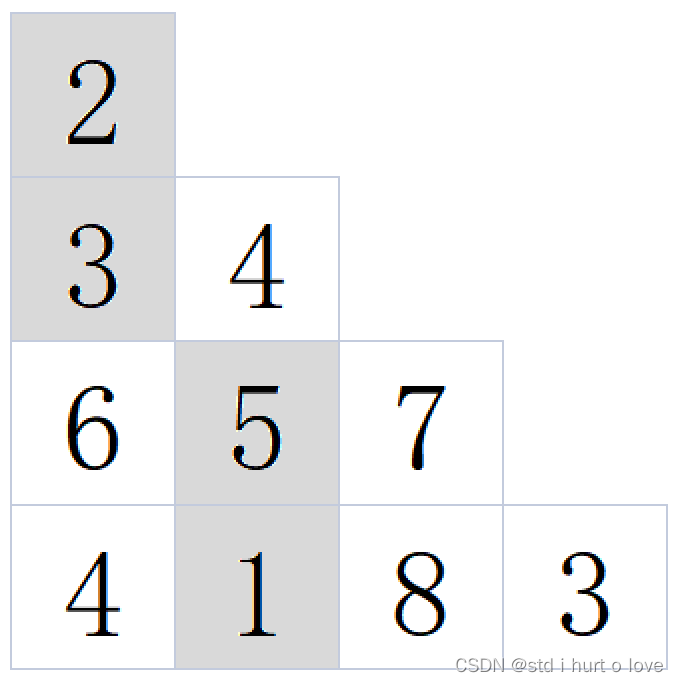
4

例如当输入[[2],[3,4],[6,5,7],[4,1,8,3]]时，对应的输出为11，
所选的路径如下图所示：
示例1
输入：
[[10]]
复制
返回值：
10
复制
示例2
输入：
[[2],[3,4],[6,5,7],[4,1,8,3]]
复制
返回值：
11
复制
说明：
最小路径是 2 ， 3 ，5 ， 1
示例3
输入：
[[1],[-1000,0]]
复制
返回值：
-999

解法一:动态规划

在这里插入代码片

定义二维 dp 数组，将解法二中「自顶向下的递归」改为「自底向上的递推」。
1、状态定义：
dp[i][j] 表示从点 (i,j) 到底边的最小路径和。
2、状态转移：
dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]

复杂度分析
时间复杂度：O(N^2)，N 为三角形的行数。
空间复杂度：O(N^2)，N 为三角形的行数。

  */
    int minTrace(vector<vector<int> >& triangle) {
    
        int n = triangle.size();
        // dp[i][j] 表示从点 (i, j) 到底边的最小路径和。
        vector<vector<int> > dp(n + 1, vector<int>(n + 1));
        // 从三角形的最后一行开始递推。
        for (int i = n - 1; i >= 0; i--) {
    
            for (int j = 0; j <= i; j++) {
    
                dp[i][j] = min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle[i][j];
            }
        }
        return dp[0][0];
    }

动态规划解法优化

空间优化
在上述代码中，我们定义了一个 N 行 N 列 的 dp 数组（N 是三角形的行数）。
但是在实际递推中我们发现，计算 dp[i][j] 时，只用到了下一行的 dp[i+1][j] 和 dp[i+1][j+1]。
因此 dp 数组不需要定义 N 行，只要定义 1 行就阔以啦。
所以我们稍微修改一下上述代码，将 i 所在的维度去掉（如下），就可以将 O(N^2)的空间复杂度优化成 O(N) 啦～
 
复杂度分析
时间复杂度：O(N^2)，N 为三角形的行数。
空间复杂度：O(N)，N 为三角形的行数。

 int minTrace(vector<vector<int> >& triangle) {
    
        int n = triangle.size();
        vector<int> dp(n + 1);
        for (int i = n - 1; i >= 0; i--) {
    
            for (int j = 0; j <= i; j++) {
    
                dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j];
            }
        }
        return dp[0];
    }

二、连续子数组最大和

解法1 动态规划

定义 dp[i]为前 i 个数中，以第 i个数结尾的子数组最大连续和。

于是有转移方程：

dp[i]=max(dp[i−1]+a[i],a[i])

其中，前面部分代表选择前面的区间的最大值，后面部分代表直接选择a[i]。

最终答案是所有的 dp[i]的最大值。

#include<bits/stdc++.h>
using namespace std;
long long a[101010],dp[101010];
int main(){
    
    int n,i;
    cin>>n;
    for(i=1;i<=n;i++)cin>>a[i];
    dp[0]=-1e9;
    long long res=-1e9;
    for(i=1;i<=n;i++){
    
        dp[i]=max(dp[i-1]+a[i],a[i]);
        res=max(res,dp[i]);
    }
    cout<<res;
    
}

解法2 贪心

我们用一个变量维护到当前位置的最大和，当加到负数的时候我们就可以把它置为0，因为显然负数再往后加会让答案变小。最终维护这个变量的最大值即可。

这种做法需要特判所有数均为负数的情况。这种情况直接输出绝对值最小的那个负数就行了。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
ll dp[101010];
ll a[101010];
int main(){
    
    int n,i;
    cin>>n;
    int jud=0;
    for(i=1;i<=n;i++){
    cin>>a[i];if(a[i]>=0)jud=1;}
    if(!jud){
    
        ll res=-1e9;
        for(i=1;i<=n;i++)res=max(res,a[i]);
        cout<<res;
        return 0;
    }
    ll res=a[1],sum=max(0LL,a[1]);
    for(i=2;i<=n;i++){
    
        sum=max(0LL,sum+a[i]);
        res=max(res,sum);
    }
    cout<<res;
}