二叉树（构造篇）

二叉树（纲领篇），先复述一下前文总结的二叉树解题总纲：

1. 是否可以通过遍历一遍二叉树得到答案？ 如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。
2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？ 如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

二叉树的构造问题一般都是使用「分解问题」的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树。

构造最大二叉树

力扣第 654 题「 最大二叉树」

每个二叉树节点都可以认为是一棵子树的根节点，对于根节点，首先要做的当然是把想办法把自己先构造出来，然后想办法构造自己的左右子树。

所以，我们要遍历数组把找到最大值 maxVal，从而把根节点 root 做出来，然后对 maxVal 左边的数组和右边的数组进行递归构建，作为 root 的左右子树。

class Solution {
    
    public TreeNode constructMaximumBinaryTree(int[] nums) {
    
        return build(nums,0,nums.length);

    }
    // 定义：将 nums[lo..hi] 构造成符合条件的树，返回根节点
    public TreeNode build(int[] nums,int left,int right){
    
         // base case
        if(left>=right) return null;
        int maxPo=-1;
        int max=-1;
        // 找到数组中的最大值和对应的索引
        for(int i=left;i<right;i++){
    
            if(nums[i]>max){
    
                max=nums[i];
                maxPo=i;
            }
        }
        // 先构造出根节点
        TreeNode root=new TreeNode(max);
        // 递归调用构造左右子树
        root.left=build(nums,left,maxPo);
        root.right=build(nums,maxPo+1,right);
        return root;
    }
}

通过前序和中序遍历结果构造二叉树

力扣第 105 题「 从前序和中序遍历序列构造二叉树」

class Solution {
    
    Map<Integer,Integer> inMap=new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
    
        int n=preorder.length;
        for(int i=0;i<n;i++){
    
            inMap.put(inorder[i],i);
        }
        return build(preorder,inorder,0,n-1,0,n-1);

    }
    public TreeNode build(int[] preorder,int[] inorder,int prel,int prer,int inl,int inr){
    
        //不能用=符号，因为prel和prer当前都没用过
        if(prel>prer) return null;
        //构建根节点
        TreeNode root=new TreeNode(preorder[prel]);
        //在中序遍历中找到根节点的位置
        int po=inMap.get(preorder[prel]);
        //找到前序遍历root左节点还有多少个
        int leftNum=po-inl;
        root.left=build(preorder,inorder,prel+1,prel+leftNum,inl,po-1);
        root.right=build(preorder,inorder,prel+leftNum+1,prer,po+1,inr);
        return root;

    }
}

通过后序和中序遍历结果构造二叉树

力扣第 106 题「 从后序和中序遍历序列构造二叉树」：

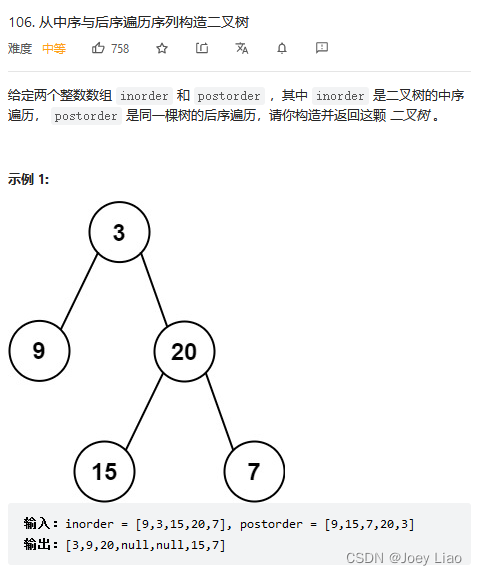
这道题和上一题的关键区别是，后序遍历和前序遍历相反，根节点对应的值为 postorder 的最后一个元素。

整体的算法框架和上一题非常类似，我们依然写一个辅助函数 build：

// 存储 inorder 中值到索引的映射
HashMap<Integer, Integer> valToIndex = new HashMap<>();

TreeNode buildTree(int[] inorder, int[] postorder) {
    
    for (int i = 0; i < inorder.length; i++) {
    
        valToIndex.put(inorder[i], i);
    }
    return build(inorder, 0, inorder.length - 1,
                 postorder, 0, postorder.length - 1);
}

/* build 函数的定义： 后序遍历数组为 postorder[postStart..postEnd]， 中序遍历数组为 inorder[inStart..inEnd]， 构造二叉树，返回该二叉树的根节点 */
TreeNode build(int[] inorder, int inStart, int inEnd,
               int[] postorder, int postStart, int postEnd) {
    

    if (inStart > inEnd) {
    
        return null;
    }
    // root 节点对应的值就是后序遍历数组的最后一个元素
    int rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    int index = valToIndex.get(rootVal);
    // 左子树的节点个数
    int leftSize = index - inStart;
    TreeNode root = new TreeNode(rootVal);



    // 递归构造左右子树
    root.left = build(inorder, inStart, index - 1,
                        postorder, postStart, postStart + leftSize - 1);
    
    root.right = build(inorder, index + 1, inEnd,
                        postorder, postStart + leftSize, postEnd - 1);
    return root;
}

通过后序和前序遍历结果构造二叉树

力扣第 889 题「 根据前序和后序遍历构造二叉树」

通过前序中序，或者后序中序遍历结果可以确定唯一一棵原始二叉树，但是通过前序后序遍历结果无法确定唯一的原始二叉树。

不过话说回来，用后序遍历和前序遍历结果还原二叉树，解法逻辑上和前两道题差别不大，也是通过控制左右子树的索引来构建：

1. 首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值。

2. 然后把前序遍历结果的第二个元素作为左子树的根节点的值。

3. 在后序遍历结果中寻找左子树根节点的值，从而确定了左子树的索引边界，进而确定右子树的索引边界，递归构造左右子树即可。

class Solution {
    
    // 存储 postorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
    
        for (int i = 0; i < postorder.length; i++) {
    
            valToIndex.put(postorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1,
                    postorder, 0, postorder.length - 1);
    }

    // 定义：根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]
    // 构建二叉树，并返回根节点。
    TreeNode build(int[] preorder, int preStart, int preEnd,
                   int[] postorder, int postStart, int postEnd) {
    
        if (preStart > preEnd) {
    
            return null;
        }
        if (preStart == preEnd) {
    
            return new TreeNode(preorder[preStart]);
        }

        // root 节点对应的值就是前序遍历数组的第一个元素
        int rootVal = preorder[preStart];
        // root.left 的值是前序遍历第二个元素
        // 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
        // 确定 preorder 和 postorder 中左右子树的元素区间
        int leftRootVal = preorder[preStart + 1];
        // leftRootVal 在后序遍历数组中的索引
        int index = valToIndex.get(leftRootVal);
        // 左子树的元素个数
        int leftSize = index - postStart + 1;

        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        // 根据左子树的根节点索引和元素个数推导左右子树的索引边界
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                postorder, postStart, index);
        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                postorder, index + 1, postEnd - 1);

        return root;
    }
}

代码和前两道题非常类似，我们可以看着代码思考一下，为什么通过前序遍历和后序遍历结果还原的二叉树可能不唯一呢？

关键在这一句：

int leftRootVal = preorder[preStart + 1];

我们假设前序遍历的第二个元素是左子树的根节点，但实际上左子树有可能是空指针，那么这个元素就应该是右子树的根节点。由于这里无法确切进行判断，所以导致了最终答案的不唯一。

至此，通过前序和后序遍历结果还原二叉树的问题也解决了。

最后呼应下前文，二叉树的构造问题一般都是使用「分解问题」的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树。先找出根节点，然后根据根节点的值找到左右子树的元素，进而递归构建出左右子树。