当前位置:网站首页>2022牛客暑期多校训练营4(ADHKLMN)
2022牛客暑期多校训练营4(ADHKLMN)
2022-08-02 08:48:00 【Tan_Yuu】
题集链接;
视频题解;
目录:
A Task Computing
数学,dp
题意
从 n 个任务中选 m 个并任意排序,每个任务有 w , p w,p w,p 两个属性,求 ∑ i = 1 m w a i ∏ j = 0 i − 1 p a j \sum_{i=1}^{m}w_{a_i}\prod_{j=0}^{i-1}p_{a_j} ∑i=1mwai∏j=0i−1paj 的最大值;
思路
首先考虑排序的过程:
对于两元素 a x , a y a_x,a_y ax,ay ,其对答案的贡献为 R 1 = ∑ i = 1 x − 1 w a i ∏ j = 0 i − 1 p a j + w a x ∏ j = 0 x − 1 p a j + w a y p a x ∏ j = 0 x − 1 p a j + ∑ i = y + 1 m w a i ∏ j = 0 i − 1 p a j R_1=\sum_{i=1}^{x-1}w_{a_i}\prod_{j=0}^{i-1}p_{a_j}+w_{a_x}\prod_{j=0}^{x-1}p_{a_j}+w_{a_y}p_{a_x}\prod_{j=0}^{x-1}p_{a_j}+\sum_{i=y+1}^{m}w_{a_i}\prod_{j=0}^{i-1}p_{a_j} R1=∑i=1x−1wai∏j=0i−1paj+wax∏j=0x−1paj+waypax∏j=0x−1paj+∑i=y+1mwai∏j=0i−1paj ;
对于两元素 a y , a x a_y,a_x ay,ax ,其对答案的贡献为 R 2 = ∑ i = 1 y − 1 w a i ∏ j = 0 i − 1 p a j + w a y ∏ j = 0 y − 1 p a j + w a x p a y ∏ j = 0 y − 1 p a j + ∑ i = x + 1 m w a i ∏ j = 0 i − 1 p a j R_2=\sum_{i=1}^{y-1}w_{a_i}\prod_{j=0}^{i-1}p_{a_j}+w_{a_y}\prod_{j=0}^{y-1}p_{a_j}+w_{a_x}p_{a_y}\prod_{j=0}^{y-1}p_{a_j}+\sum_{i=x+1}^{m}w_{a_i}\prod_{j=0}^{i-1}p_{a_j} R2=∑i=1y−1wai∏j=0i−1paj+way∏j=0y−1paj+waxpay∏j=0y−1paj+∑i=x+1mwai∏j=0i−1paj ;
两式做差得(除 a x , a y a_x,a_y ax,ay 外,上式x=下式y,上式y=下式x):
( w a x + w a y P a x − w a y − w a x P a y ) ∏ j = 0 x − 1 p a j (w_{a_x}+w_{a_y}P_{a_x}-w_{a_y}-w_{a_x}P_{a_y})\prod_{j=0}^{x-1}p_{a_j} (wax+wayPax−way−waxPay)j=0∏x−1paj
其中连乘式与顺序无关;
若使 在排序时 x 在 y 前,则依据上式大于等于0构造排序函数即可;
在排序后,逆序DP处理出结果最大的连续 m 个数;
逆序处理是因为逆序处理更容易维护公式的结果;
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
pair<double,double>pii[100005];
double dp[100005][21];
bool cmp(pair<double,double> a,pair<double,double> b)
{
return a.first+a.second*b.first>=b.first+b.second*a.first;
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++)
{
scanf("%lf",&pii[i].first);
}
for(int i=0;i<n;i++)
{
scanf("%lf",&pii[i].second);
pii[i].second/=10000;
}
sort(pii,pii+n,cmp);
// for(int i=0;i<n;i++)
// printf("%lf %lf\n",pii[i].first,pii[i].second);
for (int i = n-1; i >= 0; i--) {
for (int j = 0; j <= m; j++) {
dp[i][j] = max(dp[i][j], dp[i + 1][j]);
if (j) {
dp[i][j] = max(dp[i][j], dp[i + 1][j - 1] * pii[i].second + pii[i].first);
}
}
}
printf("%.10lf",dp[1][m]);
}
D Jobs (Easy Version)
数据结构
题意
有n家公司,每家公司有 m i m_i mi 个岗位,每个岗位对三个能力分别有数值要求,必须三个能力都达标才能获得这个岗位,如果某人获得某公司的任意一个岗位则称该人获得了该公司的工作;
有 q 次询问,由题给代码得出该人的三个能力值,求这个人可以获得多少个公司的工作;
思路
使用三维数组记录;
对于 n e e d [ i ] [ j ] [ k ] need[i][j][k] need[i][j][k] 存储对于第 i 家公司,前两个能力值分别为 j,k 时,第三个能力值所要求的最小值;
对于第 i 个公司接收到的新岗位 ( j , k , l ) (j,k,l) (j,k,l) ,则 n e e d [ i ] [ j ] [ k ] = min ( n e e d [ i ] [ j ] [ k ] , l ) need[i][j][k]=\min(need[i][j][k],l) need[i][j][k]=min(need[i][j][k],l) ;
在一个公司接收结束后,维护数组(详见代码);
代码
队友代码如下
#include <bits/stdc++.h>
using namespace std;
unsigned seed;
const int M = 998244353;
long long qm(long long a, long long b = M - 2) {
long long ans = 1;
for (; b; b >>= 1) {
if (b & 1) ans = a * ans % M;
a = a * a % M;
}
return ans;
}
int need[10][401][401];
int main() {
cin.tie(0)->sync_with_stdio(false);
int n, q;
cin >> n >> q;
memset(need, 0x3f, sizeof(need));
for (int i = 0; i < n; i++) {
int k;
cin >> k;
while (k--) {
int a, b, c;
cin >> a >> b >> c;
need[i][a][b] = min(need[i][a][b], c);
}
for (int a = 1 ; a <= 400 ; a ++ ) {
for (int b = 1 ; b <= 400 ; b ++ ) {
need[i][a][b] = min({
need[i][a][b], need[i][a][b - 1], need[i][a - 1][b]});
}
}
}
cin >> seed;
auto solve = [&](int IQ, int EQ, int AQ) -> int {
int ans = 0;
for (int i = 0; i < n; i++) {
ans += need[i][IQ][EQ] <= AQ ? 1 : 0;
}
return ans;
};
std::mt19937 rng(seed);
std::uniform_int_distribution<> u(1, 400);
int lastans = 0;
long long ans = 0;
for (int i = 1; i <= q; i++) {
int IQ =
(u(rng) ^ lastans) % 400 + 1; // The IQ of the i-th friend
int EQ =
(u(rng) ^ lastans) % 400 + 1; // The EQ of the i-th friend
int AQ =
(u(rng) ^ lastans) % 400 + 1; // The AQ of the i-th friend
lastans = solve(IQ, EQ, AQ); // The answer to the i-th friend
ans += lastans * qm(seed, q - i);
ans %= M;
}
cout << ans << '\n';
}
H Wall Builder II
贪心
题意
给定 n 个 1*1 的矩形,n-1 个 1*2 的矩形,n-2 个 1*3 的矩形,…,1 个 1*n 的矩形,将这些矩形拼成一个大矩形,求大矩形的最小周长和拼接方案;
思路
首先考虑大矩形形状越接近正方形周长越小,我们从正方形开始寻找整数 w , h w,h w,h 使得 w h = S wh=S wh=S ;
对于找到的 w , h w,h w,h 使用贪心的策略依次填满每一层即可;
即对于每一层,优先放能放进的最长的,再次放能放进剩余部分的最长的,循环至填满该层;
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n;
struct node
{
int xl, yl, xr, yr;
int id;
} block[100005];
bool cmp(node a, node b) {
return a.id < b.id; }
signed main()
{
cin >> t;
while (t--)
{
cin >> n;
multiset<int> mts;
long long sqr = 0;
for (int i = 1; i <= n; i++)
{
sqr += 1ll * i * (n - i + 1);
}
for (int i = n; i >= 1; i--)
{
for (int j = 1; j <= (n - i + 1); j++)
{
mts.insert(i);
}
}
long long cmx = 100005;
int h = 0, w = 0;
for(int i=sqrt(sqr)+1e-5;i;i--)
{
if (sqr % i == 0)
{
if ((i + (sqr / i)) * 2 <= cmx)
{
h = i;
w = sqr / i;
cmx = i * 2 + sqr * 2 / i;
break;
}
}
}
printf("%lld\n", cmx);
int cblk = 0;
for (int i = 0; i < h; i++)
{
long long width = 0;
while (width != w)
{
auto sp = mts.lower_bound(w - width);
if (sp == mts.end())
sp--;
cblk++;
block[cblk].xl = width;
block[cblk].yl = i;
block[cblk].xr = width + *sp;
block[cblk].yr = i + 1;
block[cblk].id = *sp;
width += *sp;
mts.erase(sp);
}
}
sort(block + 1, block + cblk + 1, cmp);
for (int i = 1; i <= cblk; i++)
{
printf("%lld %lld %lld %lld\n", block[i].xl, block[i].yl, block[i].xr, block[i].yr);
}
}
}
K NIO’s Sword
数学
题意
初始有一把攻击力为0的剑,需要击杀n个(1~n)敌人,仅当攻击力与 i 在模 n 意义下同余时才能击杀第 i 个敌人,玩家可以升级剑,问最少需要几次升级;
“升级”:对于当前攻击力 x ,升级一次后的攻击力为 10 x + b ( b = 0 , 1 , 2 , … , 9 ) 10x+b\ (b=0,1,2,\dots,9) 10x+b (b=0,1,2,…,9) ;
思路
考虑第 i 关的初始值一定与 i-1 在 n 意义下同余,那么每一关的选择不存在后效性,便可以逐关寻找本关最优解;
对于第 i 关的通关值x,一定满足:
x = k n + i x ∈ [ 1 0 p ( i − 1 ) , 1 0 p i ) x=kn+i\\ x\in[10^p(i-1),10^pi) x=kn+ix∈[10p(i−1),10pi)
此时的p即为升级次数,若使当前的p最小,则需要找到最小的满足条件的k;
枚举 p ,对于每个 p 计算出满足第一给条件的最小 k ,再代回判断是否满足第二个条件即可;
对于 p,i ,k有
k ⩾ 1 0 p ( i − 1 ) − i n k\geqslant\frac{10^p(i-1)-i}n k⩾n10p(i−1)−i
注意对 n = 1 n=1 n=1 的特判,此时答案为 0 ,赛时判瞎了;
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M = 998244353;
const ll inf = 0x3f3f3f3f3f3f3f3f;
ll ten[10]={
1,10,100,1000,10000,100000,1000000,10000000,100000000,1000000000};
int main()
{
ll n;
cin>>n;
if(n==1)
{
printf("0");
return 0;
}
int ans=1;
for(int i=2;i<=n;i++)
{
for(int k=1;k<=6;k++)
{
ll r=ten[k]*(i-1);
ll kk=(r-i)/n+((r-i)%n!=0);
if(kk*n+i<ten[k]*i)
{
ans+=k;
break;
}
}
}
cout<<ans;
return 0;
}
L Black Hole
计算几何、模拟
题意
求边长为a的凸正n面体收缩k次后的面数和边长;
收缩:将原凸体的临面连心线作为棱形成新的凸体;
思路
正n面体只有五种(4,6,8,12,20),并且在收缩过程中有转换关系( 4 → 4 , 6 → 8 , 8 → 6 , 12 → 20 , 20 → 12 4\to4,6\to8,8\to6,12\to20,20\to12 4→4,6→8,8→6,12→20,20→12);
找到(看题解)这五种正n面体边长与连心线长的关系即可模拟;
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M = 998244353;
const ll inf = 0x3f3f3f3f3f3f3f3f;
int main()
{
int t;
cin >> t;
while (t--)
{
int n, k;
double a;
cin>>n>>a>>k;
if(n==4||n==6||n==8||n==12||n==20)
{
printf("possible ");
while(k--)
{
if(n==4)
{
a=a/3;
}
else if(n==6)
{
n=8,a=a/sqrt(2);
}
else if(n==8)
{
n=6,a=a*sqrt(2)/3;
}
else if(n==12)
{
n=20,a=a*(3*sqrt(5)+5)/10;
}
else if(n==20)
{
n=12,a=a*(sqrt(5)+1)/6;
}
}
printf("%d %.8lf\n",n,a);
}
else printf("impossible\n");
}
return 0;
}
M Monotone Chain
计算几何
题意
给定一条折线,求一条有向直线使得折线上各点在其上的投影点是非减的(不与有向直线反向);
思路
我们考虑若干非零向量:
对于每条向量,有向直线的方向向量必须存在于该向量顺逆时针90°的范围内,即最终方向向量的可行范围是每条向量的可行范围的交集;
由此我们可以维护可行的向量两界,如果最终向量两界合法,则输出任意一界即可;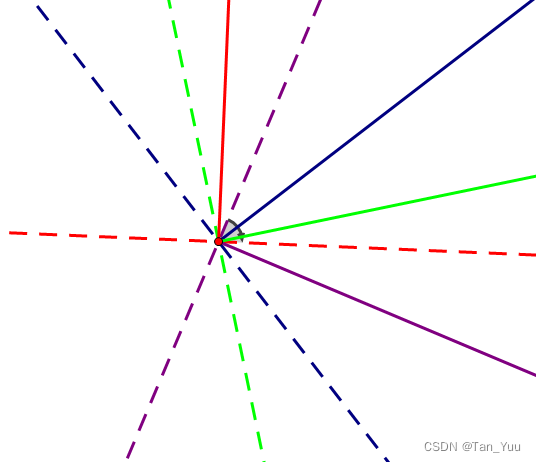
特判:
若当前可行范围是平角,并且新向量与可行范围对应的向量方向相反,此时可行范围便仅剩方向相反的两条有向直线;
这种情况不太方便使用可行范围两界维护,需要特殊处理,在代码中对应的是bool only;pair<Point, Point> oq;两变量所维护;
最开始补题时打算用与x+夹角维护,最后在找整数点输出时遇到了问题;
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M = 998244353;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double PI = acos(-1.0);
int sign(double x) // 符号函数
{
if (fabs(x) < eps)
return 0;
if (x < 0)
return -1;
return 1;
}
struct Point
{
double x, y;
Point(double a = 0, double b = 0) {
x = a, y = b; }
Point operator+(const Point &a) const {
return Point(x + a.x, y + a.y); }
Point operator-(const Point &a) const {
return Point(x - a.x, y - a.y); }
Point operator*(const double &a) const {
return Point(x * a, y * a); }
Point operator/(const double &a) const {
return Point(x / a, y / a); }
bool operator==(const Point &a) const {
return !sign(x - a.x) && !sign(y - a.y); }
bool operator<(const Point &a) const {
return (fabs(x - a.x) < eps) ? (y < a.y) : (x < a.x); }
};
double dot(Point a, Point b) {
return a.x * b.x + a.y * b.y; }
double cross(Point a, Point b) {
return a.x * b.y - b.x * a.y; }
double get_length(Point a) {
return sqrt(dot(a, a)); }
double get_angle(Point a, Point b) {
return acos(dot(a, b) / get_length(a) / get_length(b)); }
Point p[100005];
int main()
{
int n;
bool only = 0, cg = 0;
int init = 0;
cin >> n;
pair<Point, Point> que = {
Point(), Point()};
pair<Point, Point> oq = {
Point(), Point()};
Point bas = Point(PI, PI);
for (int i = 1; i <= n; i++)
{
scanf("%lf%lf", &p[i].x, &p[i].y);
if (p[i] == p[i - 1])
continue;
if (i >= 2 && !init)
bas = p[2] - p[1], init = i, que = {
Point(bas.y, -bas.x), Point(-bas.y, bas.x)};
Point tmp = p[i] - p[i - 1];
Point nowf = Point(tmp.y, -tmp.x), nows = Point(-tmp.y, tmp.x);
if (init && init != i && !only)
{
if (!cg && !sign(fabs(get_angle(tmp, bas)) - PI) )
{
only = 1;
if (que.first == Point(bas.y, -bas.x))
oq.first = que.first;
if (que.second == Point(-bas.y, bas.x))
oq.second = que.second;
cg = 1;
}
else
{
if (cross(que.second, nows) < 0)
que.second = nows;
if (cross(que.first, nowf) > 0)
que.first = nowf;
cg = 1;
}
}
else if (only)
{
if (sign(get_length(oq.first)) && sign(dot(tmp, oq.first)) < 0)
oq.first = Point();
if (sign(get_length(oq.second)) && sign(dot(tmp, oq.second)) < 0)
oq.second = Point();
}
}
// printf("*%d\n",only);
// if(only){
// printf("*%lf %lf %lf %lf\n",oq.first.x,oq.first.y,oq.second.x,oq.second.y);
// }
// else
// {
// printf("*%lf %lf %lf %lf\n",que.first.x,que.first.y,que.second.x,que.second.y);
// }
if (!init && !sign(get_length(bas - Point(PI, PI))) || !sign(get_length(bas)))
{
printf("YES\n0 0 1 0");
}
else if ((!only && sign(cross(que.second, que.first)) <= 0) && dot(que.second, que.first) > 0 ||
(only && (sign(get_length(oq.first)) || sign(get_length(oq.second)))))
{
printf("YES\n0 0 ");
if (only && sign(get_length(oq.first)))
printf("%d %d", (int)oq.first.x, (int)oq.first.y);
else if (only && sign(get_length(oq.second)))
printf("%d %d", (int)oq.second.x, (int)oq.second.y);
else
printf("%d %d", (int)que.second.x, (int)que.second.y);
}
else
{
printf("NO");
}
return 0;
}
N Particle Arts
数学
题意
n个粒子,每个粒子有能量 a i a_i ai ,两两随机碰撞,碰撞发生后两粒子能量变为 a & b , a ∣ b a\&b,a|b a&b,a∣b ,经过很多次碰撞后,所有粒子能量会趋于稳定,求能量稳定后粒子能量的方差;
思路
经过模拟空想,粒子能量二进制位上的1和0会“富集”到某些数上,并且每位上的1总数不变;
例如样例
001b
010b
011b
100b
101b
“富集”后便成为了如下形式:
000b
000b
001b
111b
111b
即1会“聚集”在或结果上,0也会“聚集”在与结果上;
依此我们可以求出新数列,并计算方差;
代码
队友代码如下
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
void print(__int128_t x) {
vector<char> buff;
while (x) {
buff.push_back(x % 10 + '0');
x /= 10;
}
for (int i = buff.size() - 1; i >= 0; i--) {
cout << buff[i];
}
}
int main() {
int n;
cin >> n;
vector<int> u(n);
vector final(15, 0);
for (auto &x : u) cin >> x;
for (auto &x : u) {
for (int i = 0; i < 15; i++) {
if ((x >> i) & 1) {
final[i]++;
}
}
}
for (int i = 0; i < n; i++) {
u[i] = 0;
for (int j = 0; j < 15; j++) {
if (i < final[j]) u[i] |= 1 << j;
}
}
__int128_t sum = 0;
__int128_t a = 0;
for (auto x : u) sum += x;
for (auto x : u) a += (1ll * n * x - sum) * (1ll * n * x - sum);
__int128_t b = 1ll * n * n * n;
auto x = __gcd(a, b);
a /= x, b /= x;
if (a == 0 || b == 0) {
cout << "0/1\n";
return 0;
}
print(a);
putchar('/');
print(b);
return 0;
}
ed
计算几何专题,搞了一学期的计算几何只是让补题方便了些(
边栏推荐
猜你喜欢

三维体尺测量

MySQL Workbench 安装及使用

SVN下载上传文件
location对象,navigator对象,history对象学习

Bigder:41/100生产bug有哪些分类
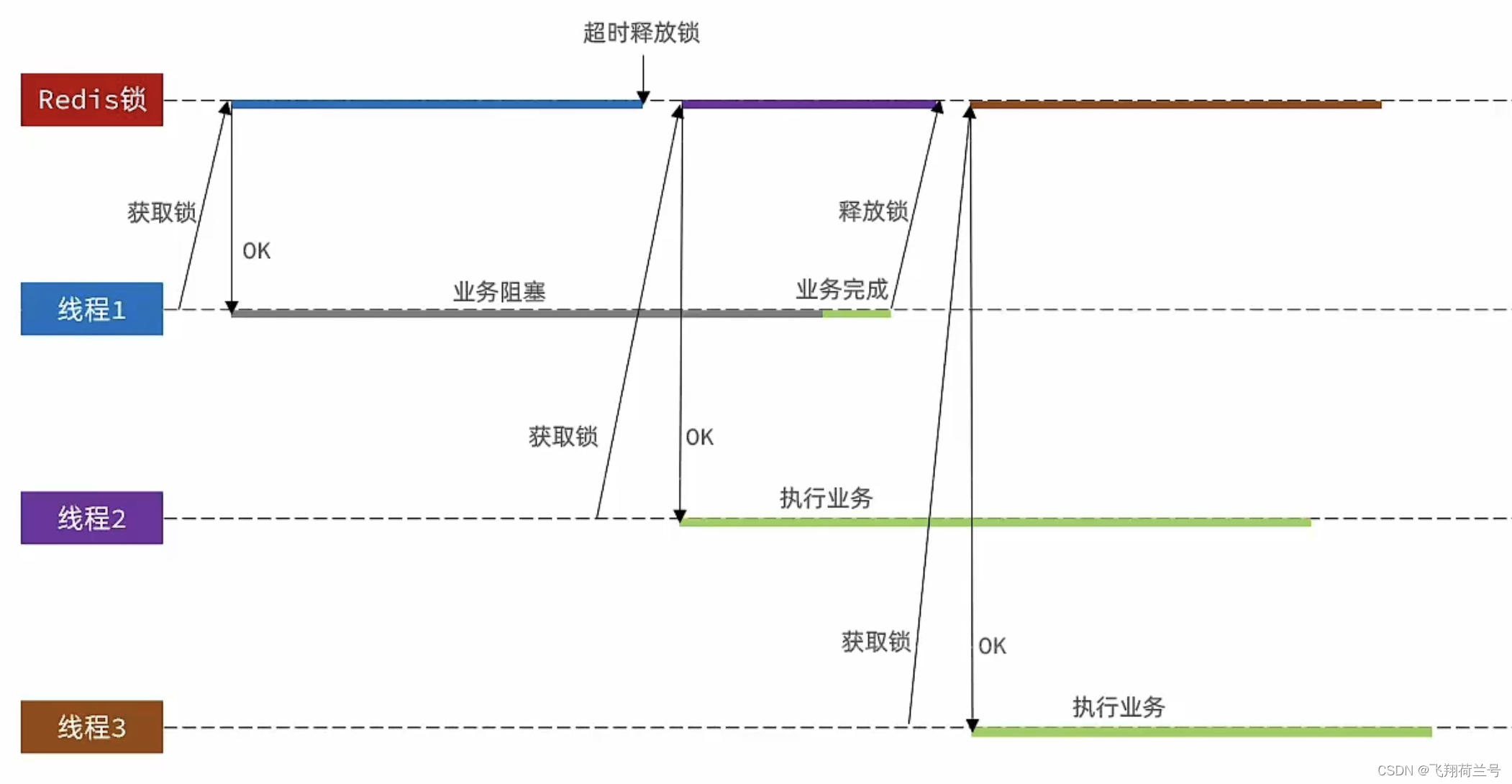
Redis分布式锁

Qt读取文件中内容(通过判断GBK UTF-8格式进行读取显示)

向量组的线性相关性
Business Intelligence Platform BI Business Intelligence Analysis Platform How to Choose the Right Business Intelligence Platform BI

PyQt5 (a) PyQt5 installation and configuration, read from the folder and display images, simulation to generate the sketch image
随机推荐
利用minlm比较句子之间的相似度
十大免费cms建站系统介绍推荐
postman使用方法
主流监控系统工具选型及落地场景参考
【微信小程序2】事件绑定
【论文阅读】Distilling the Knowledge in a Neural Network
文章解读 -- FlowNet3D:Learning Scene Flow in 3D Point Clouds
How Engineers Treat Open Source --- A veteran engineer's heartfelt words
初学者怎么快速学会SQL
Installation and use of pnpm
腾讯T8架构师,教你学中小研发团队架构实践PDF,高级架构师捷径
Golang ORM框架 — GORM
UVM信息服务机制
WebGPU 导入[1] - 入门常见问题与个人分享
Redisson实现分布式锁
redis-desktop-manager下载安装
抓包工具Charles修改Response步骤
破解wifi密码 暴力破解 保姆式教学
Redis分布式锁
Fiddler(七) - Composer(组合器)克隆或者修改请求