当前位置:网站首页>“蔚来杯“2022牛客暑期多校训练营4
“蔚来杯“2022牛客暑期多校训练营4
2022-08-02 08:18:00 【Bold!】
N.Particle Arts
题意:
给出n个粒子,每个粒子带有ai的能量,当能量为a的粒子和能量为b
的粒子相互碰撞时,原来的两个粒子会毁灭,产生两个新的
能量分别为a&b和a|b的粒子。经过一段时间后,这些粒子的
方差会收敛到一个固定值,求出这个固定值。
思路:
位运算,思维题。
每一位的1的总数是不变的,要使得最后收敛,
那么就将多的1尽可能的分散到其他数为0的那位上,使1尽可能地集中到一个数上去。
考虑到平均数可能为分数,因此先将式子变下型。
原本应该是(b[i]-s/n)(b[i]-s/n)/n
为了避免分数,将里面的n提出来,就变成了
(b[i]n-s)(b[i]n-s)/(nnn)。
再求分子分母的gcd,最后输出除以gcd之后的分数形式。
分母是1还是应该输出。
ll开不了的时候就试一试__int128,输入输出要自己写
__int128
代码:
(1)用的是(b[i]n-s)(b[i]n-s)/(nn*n)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int __int128//定义int
const int N=1e5+7;
int gcd(int a,int b) {
return b>0 ? gcd(b,a%b):a;
}
ll n,x;
int b[N],w[25],s,ans;
void print(int x)//__int128的输出需要单独写函数
{
if(x>=10)
{
print(x/10);
cout << (long long)(x%10);
}
if(x<10)
{
cout << (long long)(x);
return ;
}
}
signed main(){//前面用了#define int __int128,这里就要用signed main
cin>>n;
for(int i=1;i<=n;i++){
cin>>x;
s+=x;
for(int j=0;j<20;j++){
if((x>>j)&1) w[j]++;//这一位上的位数加1
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<20;j++){
if(w[j]>0) {
b[i]+=(1<<j);
w[j]--;
}
}
ans+=(b[i]*n-s)*(b[i]*n-s);
}
int x=ans,y=n*n*n;
int g=gcd(x,y);
print(x/g);
cout<<"/";
print(y/g);
return 0;
}
(2)用了计算方差的变形公式。
S2=[(x12+x22+…+xn^2) −( (x1+x2+…+xn)^2)/n]/n
再将里面的n提出来,就变成了分子为ansn-ss,分母为n*n,再求gcd。
用了这个变形公式开ll就可以过,但是上面那个就不行。我也不知道是不是因为上面那个出现了n^3的缘故。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N =1e6+10;
ll gcd(ll a,ll b){
return b>0?gcd(b,a%b):a;
}
ll n,x;
ll b[N],w[20],s,ans;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(ll i=1;i<=n;i++){
cin>>x;
s+=x;
for(ll j=0;j<20;j++){
if((x>>j)&1) w[j]++;
}
}
for(ll i=1;i<=n;i++){
for(ll j=0;j<20;j++){
if(w[j]){
b[i]+=(1<<j);
w[j]--;
}
}
ans+=b[i]*b[i];
}
ll x=n*ans-s*s,y=n*n;
ll g=gcd(x,y);
printf("%lld/%lld\n",x/g,y/g);
return 0;
}
K.NIO’s Sword
题意:
NIO初始攻击值为A=0.有n个敌人,需要按顺序将他们杀死。
对于第i个敌人,当A≡i(mod n)时才能杀死他。
NIO可以随时升级攻击力,任选一个0-9之间的数x,
将A变成A*10+x。
NIO想要最小化升级次数以便能够尽快地赢得比赛,
问最小次数是多少?
思路:
代码:
#include <bits/stdc++.h>
using namespace std;
ll n,ans,a[10]={1,10,100,1000,10000,100000,1000000};//a数组存放乘的数
int main(){
scanf(“%d”,&n);
if(n==1) {//特判n=1时,输出0
printf(“0”);
return 0;
}
for(ll i=1;i<=n;i++){//枚举i
ll k;
for( k=1;k<=6;k++){//因为n的范围在1e6之内,所以最多升级6次
ll x=((i-a[k]*(i-1))%n+n)%n;//因为可能减了之后为负数,因此先模再+n再取余
if(x<a[k]) break;//如果找到了小于a[k]的数,就退出循环,累计这个k
}
ans+=k;
}
printf(“%d\n”,ans);
return 0;
}
D.Jobs (Easy Version)
题意:
有n个公司,每个公司有mi个职位,q个朋友,当EQ,IQ,AQ均达到limit时才能得到offer,先求出每个朋友得到的offer数,再根据给出的公式累计答案。
思路:
因为对于每个职位,评判标准有3个,因此采用三维前缀和。又因为想到对于每个职位,都只能是得到offer和不得到两种情况,因此想到0,1,用二进制,bitset开三维数组,先预处理出f三维数组,然后对于每个人由随机数种子产生的三商对应的f数组来看看里面的1的个数,累计答案。
三维前缀和 容斥原理 s(x,y,z)=a(x,y,z)+s(x,y,z-1)+s(x,y-1,z)+s(x-1,y,z)
-s(x-1,y-1,z)-s(x-1,y,z-1)-s(x.y-1,z-1)+s(x-1,y-1,z-1);如果是开的bitset数组,每位只能为0或1,那么用|即可,即 bitset<10> f[N][N][N];//定义
f[x][y][z][i]=1;//初始化
f[i][j][k]=f[i][j][k]|f[i][j][k-1]|f[i][j-1][k]|f[i-1][j][k]|f[i][j-1][k-1]|f[i-1][j][k-1]|f[i-1][j-1][k]|f[i-1][j-1][k-1];//三维前缀和
bitset
foo.size() 返回大小(位数)
foo.count() 返回1的个数
foo.any() 返回是否有1
foo.none() 返回是否没有1
foo.set() 全都变成1
foo.set(p) 将第p + 1位变成1
foo.set(p, x) 将第p + 1位变成x
foo.reset() 全都变成0
foo.reset(p) 将第p + 1位变成0
foo.flip() 全都取反
foo.flip(p) 将第p + 1位取反
foo.to_ulong() 返回它转换为unsigned long的结果,如果超出范围则报错
foo.to_ullong() 返回它转换为unsigned long long的结果,如果超出范围则报错
foo.to_string() 返回它转换为string的结果
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 401,mod=998244353;
int n,q,m,seed,x,y,z;
bitset<10> f[N][N][N];//指定大小,维数
ll qk(ll a,ll b){//快速幂
ll ans=1;
a%=mod;
b%=mod;
while(b){
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
b%=mod;
}
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=0;i<n;i++){
cin>>m;
while(m--){
cin>>x>>y>>z;
f[x][y][z][i]=1;//将第i位的f[x][y][z]置为0
}
}
for(int i=1;i<=400;i++){
for(int j=1;j<=400;j++){
for(int k=1;k<=400;k++){
//三维前缀和
f[i][j][k]=f[i][j][k]|f[i-1][j-1][k-1]|f[i][j-1][k-1]|f[i-1][j][k-1]|f[i-1][j-1][k]|f[i][j][k-1]|f[i][j-1][k]|f[i-1][j][k];
}
}
}
cin>>seed;//随机数种子
ll ans=0;
std::mt19937 rng(seed);
std::uniform_int_distribution<> u(1,400);
int lastans=0;
for (int i=1;i<=q;i++){
int IQ=(u(rng)^lastans)%400+1; // The IQ of the i-th friend
int EQ=(u(rng)^lastans)%400+1; // The EQ of the i-th friend
int AQ=(u(rng)^lastans)%400+1; // The AQ of the i-th friend
//获取匹配的个数
int x=f[IQ][EQ][AQ].count();//返回1的个数
ans=(ans+x*qk(seed,q-i)%mod)%mod;//公式
lastans=x;
}
cout<<ans<<endl;
return 0;
}
边栏推荐
- 解决IDEA安装安装插件慢问题
- QT web development - Notes - 3
- 如何建立私域流量?私域流量对企业有什么好处?
- 【C】关于柔性数组.简要的谈谈柔性数组
- BGP通过MPLS解决路由黑洞
- 力扣:第 304 场周赛
- MySQL 中 count() 和 count(1) 有什么区别?哪个性能最好?
- Biotin - LC - Hydrazide | CAS: 109276-34-8 | Biotin - LC - Hydrazide
- R language plotly visualization: plotly visualizes the scatter plot of the actual value of the regression model and the predicted value of the regression, analyzes the prediction performance of the re
- JSP页面中page指令contentPage/pageEncoding具有什么功能呢?
猜你喜欢
PostgreSQL learning summary (11) - PostgreSQL commonly used high-availability cluster solutions

PyCharm usage tutorial (more detailed, picture + text)

血气方刚的年轻小伙竟去做家政小哥,是怎样成功逆袭转行的
![Detailed explanation of calculation commands in shell (expr, (()), $[], let, bc )](/img/3c/5cc4d16b9b525997761445f32802d5.png)
Detailed explanation of calculation commands in shell (expr, (()), $[], let, bc )
![[OC学习笔记]ARC与引用计数](/img/56/033cfc15954567d63d987d91ca8d63.png)
[OC学习笔记]ARC与引用计数
Biotin-EDA|CAS:111790-37-5| 乙二胺生物素
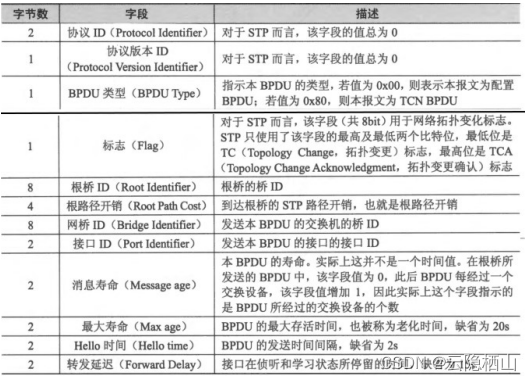
HCIP笔记十六天

Biotin - LC - Hydrazide | CAS: 109276-34-8 | Biotin - LC - Hydrazide

图扑软件数字孪生油气管道站,搭建油气运输管控平台

OneinStack多版本PHP共存
随机推荐
(Note) AXIS ACASIS DT-3608 Dual-bay Hard Disk Array Box RAID Setting
Qt读取文件中内容(通过判断GBK UTF-8格式进行读取显示)
Flink 系统性学习笔记系列
解决IDEA安装安装插件慢问题
The custom table form
【特别提醒】订阅此专栏的用户请先阅读本文再决定是否需要购买此专栏
OneinStack多版本PHP共存
day——05 迭代器,生成器
nodejs 简介
Button to control the running water light (timer)
Postman download localization of installation and use
MFC最详细入门教程[转载]
Installation and use of pnpm
MySQL 中 count() 和 count(1) 有什么区别?哪个性能最好?
力扣:第 304 场周赛
Write a small game in C (three chess)
PostgreSQL learning summary (11) - PostgreSQL commonly used high-availability cluster solutions
高仿【华为消费者业务官网】和精彩动画剖析:练习在低代码平台中嵌入JS代码
In a recent build figure SLAM, and locate the progress
测试时大量TIME_WAIT