当前位置:网站首页>State compression DP example (traveling salesman problem and rectangle filling problem)
State compression DP example (traveling salesman problem and rectangle filling problem)
2022-06-13 11:02:00 【I can screw the bottle cap when I am born again】
It's convenient to review later
Given a sheet n A weighted undirected graph of points , Point from 0∼n−1 label , Find the starting point 0 To the end point n−1 The shortest of Hamilton route .
Hamilton The definition of path is from 0 To n−1 Pass through every point exactly once without repetition or leakage .
Input format
Enter the integer in the first line n.
Next n Every line n It's an integer , Among them the first i Xing di j An integer represents a point i To j Distance of ( Write it down as a[i,j]).
For arbitrary x,y,z, Data assurance a[x,x]=0,a[x,y]=a[y,x] also a[x,y]+a[y,z]≥a[x,z].
Output format
Output an integer , Means shortest Hamilton The length of the path .
Data range
1≤n≤20
0≤a[i,j]≤107
sample input :
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
sample output :
18
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int w[N][N];
int f[M][N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
cin >> w[i][j];
memset(f, 0x3f, sizeof f);
f[1][0] = 0;
for (int i = 0; i < 1 << n; i ++ )
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
for (int k = 0; k < n; k ++ )
if (i >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][n - 1];
return 0;
}

// This kind of problem always feels like there is no way to start , All horizontal schemes are all schemes , It feels like searching , Pressure DP I feel I need to rely on experience . The state feels like the volume of the knapsack problem , Is the decision condition ,
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 12,M = 1<<N;
int n,m;
long long f[N][M];
bool st[M];
int main(){
while (cin>>n>>m,n||m)
{
// Preprocessing status Each column of consecutive null values must be an even number .
for (int i=0;i<1<<n;i++)
{
int cnt = 0;
st[i] = true;
for (int j=0;j<n;j++)
{
if (i>>j&1)
{
if (cnt&1) st[i] = false;
cnt=0;
}
else
cnt++;
}
if (cnt&1) st[i] = false;
}
memset (f,0,sizeof f);
f[0][0] = 1;
for (int i=1;i<=m;i++)
for (int j=0;j<1<<n;j++)
for (int k=0;k<1<<n;k++)
if ((j&k)==0&&st[j|k]) // No overlap ,
f[i][j] += f[i-1][k];
cout<<f[m][0]<<endl;
}
return 0;
}
边栏推荐
- Four methods of finding combinatorial numbers
- Flutter simple and excellent open source dialog uses free_ dialog
- 【20220526】UE5.0.2 release d11782b
- As a tester, these basic knowledge are essential
- QTcpServer. QTcpSocket. Differences between qudpsockets
- The road of ospo construction of Weibo: how to promote enterprise open source through ospo construction?
- Nim游戏阶梯 Nim游戏和SG函数应用(集合游戏)
- 欧拉函数和线性筛求欧拉函数
- The first laravel workflow engine released the official version of v1.0
- Finally, the monthly income is 20000!!
猜你喜欢

ue5 小知识点 geometry script modeling

Redis相关

Record several interesting XSS vulnerability discoveries

服务器的使用
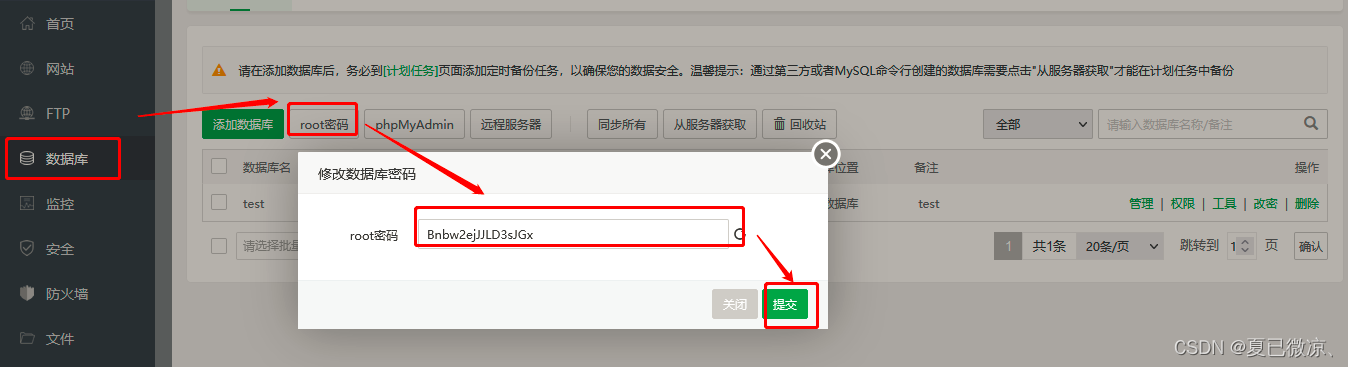
View the default MySQL password in the pagoda

音视频技术开发周刊 | 249

Database learning notes (Chapter 16)

欧拉函数和线性筛求欧拉函数

Spark source code (I) how spark submit submits jars and configuration parameters to spark server

Easyclick run code snippet out null
随机推荐
元宇宙土地:是什么让数字房地产变得有价值
MFC自定义button实现颜色控制
Private computing fat core concepts and stand-alone deployment
Gauss elimination for solving N-element equations
Redis related
2021CCPC网络赛题解加总结
SSM整合初步 所得细节
[cloud enjoying freshness] community weekly · vol.66- Huawei partners and Developers Conference 2022 wonderful agenda announcement
什么是400G以太网?
Web3 system construction: principles, models and methods of decentralization (Part I)
数位DP例题
Wechat applet customer service automatic reply - PHP implementation
Brief request process
很妙的贪心(F2. Nearest Beautiful Number (hard version))
避免让转型企业走入歧途,是时候重新理解下湖仓一体了!| Q推荐
ST表学习
Euler function and finding Euler function by linear sieve
Talk about MySQL indexing mechanism
【20220526】UE5.0.2 release d11782b
作为一个测试人员,这些基础知识必不可少