当前位置:网站首页>Matlab 6-DOF manipulator forward and inverse motion
Matlab 6-DOF manipulator forward and inverse motion
2022-06-12 06:39:00 【A building climbing pig】
MATLAB The forward and reverse motion of a 6-DOF manipulator
Realization effect
1、 Forward kinematics solution workspace

2、 Inverse kinematics solves the rotation angle

Define mathematical functions
X Axis rotation matrix (fun_dirsolu_trotx.m)
function Rx = fun_dirsolu_trotx(x,y)
if nargin > 1 && strcmp(y, 'd')
x = x *pi/180;
end
Rx=[1 0 0 0;0 cos(x) -sin(x) 0;0 sin(x) cos(x) 0;0 0 0 1];
end
Y Axis rotation matrix (fun_dirsolu_troty.m)
function Ry = fun_dirsolu_troty(y,x)
if nargin > 1 && strcmp(x, 'd')
y = y *pi/180;
end
Ry=[cos(y) 0 sin(y) 0;0 1 0 0;-sin(y) 0 cos(y) 0;0 0 0 1];
end
Z Axis rotation matrix (fun_dirsolu_trotz.m)
function Rz = fun_dirsolu_trotz(z,x)
if nargin > 1 && strcmp(x, 'd')
z = z *pi/180;
end
Rz=[cos(z) -sin(z) 0 0;sin(z) cos(z) 0 0;0 0 1 0;0 0 0 1];
end
Translation matrix (fun_dirsolu_transl.m)
function D = fun_dirsolu_transl(x,y,z)
D=[1 0 0 x;0 1 0 y;0 0 1 z;0 0 0 1];
end
Definition DH Transformation matrix function
Definition MDH Transformation matrix (fun_dirsolu_mdh.m)
% % % The main implementation : Space coordinate transformation , utilize DH Parameter Solving i-1 To i A matrix that changes in order around itself .
% % % Be careful :2018 edition MATLAB When using , Must be pi Defined as a character, it contains syms pi Statement of !!( Sometimes it is defined separately pi Will report a mistake , You can define it without a semicolon pi)
% % % For example, it just defines theta When finding the change matrix :
% % % syms theta;
% % % fun_dh(theta,0,0,pi/2)
% The result is :(4967757600021511*sin(theta))/81129638414606681695789005144064, error !!
% % % When put pi After definition :
% % % syms theta;
% % % syms pi % Do not add a semicolon at this time , Prevent error reporting .
% % % fun_dh(theta,0,0,pi/2)
% The result is :[ cos(theta), -sin(theta), 0, 0]
% % % % % [ 0, 0, -1, 0]
% % % % % [ sin(theta), cos(theta), 0, 0]
% % % % % [ 0, 0, 0, 1]
% % %----------------------------------------------------------------------------------
function T = fun_dirsolu_mdh(theta,d,a,alpha)
T = fun_dirsolu_trotx(alpha)*fun_dirsolu_transl(a,0,0)*fun_dirsolu_trotz(theta)*fun_dirsolu_transl(0,0,d);
end
Definition SDH Transformation matrix (fun_dirsolu_sdh.m)
function T = fun_dirsolu_sdh(theta,d,a,alpha)
T = fun_dirsolu_trotz(theta)*fun_dirsolu_transl(0,0,d)*fun_dirsolu_trotx(alpha)*fun_dirsolu_transl(a,0,0);
end
MDH and SDH The difference between
Refer to the connection Robotic toolbox10.2 Of fkine Function and manipulator MDH and DH Application of change matrix
Define auxiliary calculation functions
Matrix Simplification function (fun_round_matrix.m)
Matrix Simplification function , Ensure that the final effect of the matrix is numerical
function T = fun_round_matrix(A)
[a,b] = size(A);
for x = 1:a
for y = 1:b
T(x,y) = roundn(double(A(x,y)),-3);
end
end
end
auxiliary sin function (fun_revsolu_sin.m)
function s = fun_revsolu_sin(n)
d=sin(n);
if d<0.001
s = 0;
else
s=d;
end
end
auxiliary cos function (fun_revsolu_cos.m)
function c = fun_revsolu_cos(n)
d=cos(n);
if d<0.001
c = 0;
else
c=d;
end
end
Forward kinematics
1、 Definition DH Parameters
2、 To paraphrase DH matrix
3、 Solving workspaces
Master file ( Self named .m)
1、 Rotation matrix for solving joint angle
2、 For solving the forward kinematics workspace
3、 Including the call of inverse kinematics
4、 The example manipulator is KUKA Of ,DH Parameter is :

clear;clc;
syms theta1 theta2 theta3 theta4 theta5 theta6;
% % Define the manipulator DH Parameters , among L=[theta d a alpha]
L1 = [theta1, 1045, 0, 0];
L2 = [theta2, 0, 500, -pi/2];
L3 = [theta3+pi/2, 0, 1300, 0];
L4 = [theta4, 1025, 55, pi/2];
L5 = [theta5, 0, 0, pi/2];
L6 = [theta6+pi, 0, 0, -pi/2];
T01 = fun_dirsolu_mdh(L1(1),L1(2),L1(3),L1(4));
T12 = fun_dirsolu_mdh(L2(1),L2(2),L2(3),L2(4));
T23 = fun_dirsolu_mdh(L3(1),L3(2),L3(3),L3(4));
T34 = fun_dirsolu_mdh(L4(1),L4(2),L4(3),L4(4));
T45 = fun_dirsolu_mdh(L5(1),L5(2),L5(3),L5(4));
T56 = fun_dirsolu_mdh(L6(1),L6(2),L6(3),L6(4));
T06 = T01*T12*T23*T34*T45*T56;
% % Solve the transformation matrix ,T1 assignment ,round_matrix Simplify printing .
% T1=fun_round_matrix(subs(T06,{
theta1,theta2,theta3,theta4,theta5,theta6},{
1.2,0.3,1,0.2,1.5,0.8}));
% T2=fun_round_matrix(subs(T06,{
theta1,theta2,theta3,theta4,theta5,theta6},{
0,0,0,0,0,0}));
% % Find eight sets of inverse solutions .
% [S,Q] = fun_revsolu_Kuka6D(T1);
% % % % % Solving workspaces ,R assignment ,dirsolu_6D_workspace.m Draw workspace .
% R = [-pi pi;-(13/18)*pi (2/18)*pi;(-10/18)*pi (14/18)*pi;-pi pi;-pi pi;-pi pi];
% dirsolu_6D_workspace;
Forward kinematics solution workspace (dirsolu_6D_workspace.m)
1、 Monte Carlo method to solve the workspace
2、 Put the recorded points into the data , no need hold on mapping Save resources
3、 Turn on Parallel Computing
% The main implementation : Use the forward kinematics to solve the workspace .
% Be careful :( Can't run directly !)
%1、 Random function N decision lim_theta Discrete numerical range of angles ,rand(N,1) Means new N individual 0~1 The random number ,1 Express 1 Column , If 1 Change to 10 be
% yes 10 Number of columns , Every column is N individual . If in theta1 The medium use limit is [-pi,pi] So in order to make discrete lim_theta1 Also in the [-pi,pi] Between
%, So its value is -pi+2*pi*rand(N,1). Come to the conclusion X=[a,b] when , Then the discrete range X=a+(b-a)*rand(N,1);
%2、for Cyclic n Indicates the number of points when drawing the point graph ;
%3、subs Function pair syms Variable assignment , Solve end {
6} The origin of the coordinate system [0;0;0] Relative base coordinates {
0} The location of , because T06 yes 4X4 matrix ,
% So in {
6} The origin coordinates are complemented 1, use [0;0;0;1] Indicates its origin position .
if exist('T06') && exist( 'R')
point=15000;
lim_theta1=R(1,1)+(R(1,2)-R(1,1))*rand(point,1);
lim_theta2=R(2,1)+(R(2,2)-R(2,1))*rand(point,1);
lim_theta3=R(3,1)+(R(3,2)-R(3,1))*rand(point,1);
lim_theta4=R(4,1)+(R(4,2)-R(4,1))*rand(point,1);
lim_theta5=R(5,1)+(R(5,2)-R(5,1))*rand(point,1);
lim_theta6=R(6,1)+(R(6,2)-R(6,1))*rand(point,1);
parfor n=1:1:point
p=subs(T06,{
theta1 theta2 theta3 theta4 theta5 theta6},{
lim_theta1(n),lim_theta2(n), ...
lim_theta3(n),lim_theta4(n),lim_theta5(n),lim_theta6(n)})*[0;0;0;1];
q(n,:) = p;
end
q = double(q);
qx = q((1:point),1);
qy = q((1:point),2);
qz = q((1:point),3);
else
disp('---------ERROR----------')
end
% % %----------------------------------------------------------------------------------
Inverse kinematics
Mathematical derivation of inverse kinematics



Other restrictions , See the code .
Inverse kinematics function (fun_revsolu_Kuka6D.m)
Finally, the returned result is the inverse solution matrix and the number of qualified inverse solutions .
function [S,Q] = fun_revsolu_Kuka6D(T)
%FUN_REVSOLU_KUKA6D A summary of this function is shown here
% Detailed description here
r11=T(1,1);r12=T(1,2);r13=T(1,3);px=T(1,4);
r21=T(2,1);r22=T(2,2);r23=T(2,3);py=T(2,4);
r31=T(3,1);r32=T(3,2);r33=T(3,3);pz=T(3,4);
a1=500;a2=1300;a3=55;
d1=1045;d4=1025;
n=1;
theta1=atan(py/px);
c1=fun_revsolu_cos(theta1);s1=fun_revsolu_sin(theta1);
K=(px*px+py*py+(pz-d1)*(pz-d1)+a1*a1-a2*a2-a3*a3-d4*d4-2*a1*c1*px-2*a1*s1*py)/(2*a2);
KI = a3^2+d4^2-K^2;
if(KI <0 || abs(px)>2826 || abs(py)>2826 || pz >3700 || pz <-1045)
S = 0;
Q = [];
else
for i=0:1
theta3 = atan2(d4,a3)-atan2(K,(-1)^i*sqrt(abs(a3^2+d4^2-K^2)));
c3=fun_revsolu_cos(theta3);s3=fun_revsolu_sin(theta3);
ats23 = (a3-a2*s3)*(-c1*px-s1*py+a1)+(d4+a2*c3)*(-pz+d1);
atc23 = (a3-a2*s3)*(-pz+d1)+(d4+a2*c3)*(c1*px+s1*py-a1);
theta23 = atan2(ats23,atc23);
theta2 = theta23-theta3;
c2=fun_revsolu_cos(theta2);s2=fun_revsolu_sin(theta2);
s23=fun_revsolu_sin(theta2+theta3);c23=fun_revsolu_cos(theta2+theta3);
ats4 = -r13*s1+r23*c1;
atc4 = -r13*c1*s23-r23*s1*s23-r33*c23;
for j = 0:1
theta4 = atan2(ats4,atc4) + j*pi;
c4=fun_revsolu_cos(theta4);s4=fun_revsolu_sin(theta4);
ats5 = -r23*(c1*s4-c4*s1*s23)+r13*(s1*s4+c1*c4*s23)+c4*c23*r33;
atc5 = c1*c23*r13-r33*s23+c23*r23*s1;
for k =0:1
theta5 =(-1)^k*atan2(ats5,atc5);
c5=fun_revsolu_cos(theta5);s5=fun_revsolu_sin(theta5);
ats6 = r22*(c5*(c1*s4-c4*s1*s23)+c23*s1*s5)-r12*(c5*(s1*s4+c1*c4*s23)-c1*c23*s5) - r32*(s5*s23 + c4*c5*c23);
atc6 = r12*(c4*s1-c1*s4*s23)-r22*(c1*c4+s1*s4*s23)-c23*r32*s4;
theta6 = atan2(ats6,atc6);
Q(n,:) = fun_round_matrix([theta1 theta2 theta3 theta4 theta5 theta6]);
n = n+1;
end
end
end
S = 0;
for i = 1:8
if(-3.14<Q(i,1) && Q(i,1)<3.14 && -2.267<Q(i,2) && Q(i,2)<0.349 && -1.744<Q(i,3) && Q(i,3)<2.512)
if(-3.14<Q(i,4) && Q(i,4)<3.14 && -3.14<Q(i,5) && Q(i,5)<3.14 && -3.14<Q(i,6) && Q(i,6)<3.14)
S = S+1;
end
end
end
end
end
0 Integral resources
边栏推荐
- 六月集训 第九日——位运算
- Upload file (post form submission form data)
- LeetCode-884. Unusual words in two sentences
- SQL注入原理即sqli-labs搭建,sql注入简单实战
- LeetCode-1873. Calculate special bonus
- Excel VBA opens a file that begins with the specified character
- Apache poi 导入导出Excel文件
- Opencv_100问_第五章 (21-25)
- Process when solving vagrant up_ builder. rb:43:in `join‘: incompatible character encodings: GBK and UTF-8
- descheduler 二次调度让 Kubernetes 负载更均衡
猜你喜欢

LeetCode-419. Battleship on deck

Bert Chinese classification model training + reasoning + deployment

Redis problem (I) -- cache penetration, breakdown, avalanche

Meituan won the first place in fewclue in the small sample learning list! Prompt learning+ self training practice

PHP read / write cookie
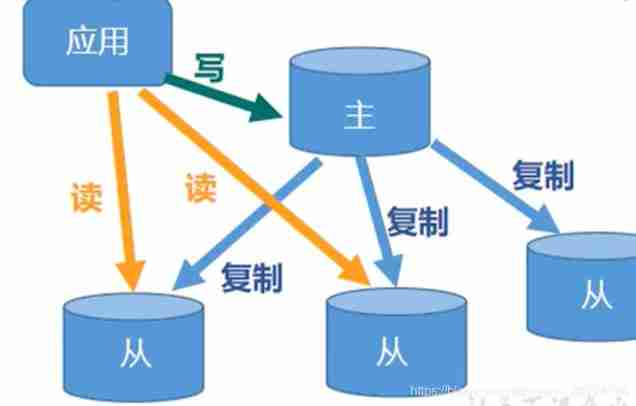
Redis configuration (III) -- master-slave replication
![Leetcode: Sword finger offer 66 Build product array [application of pre and post infix]](/img/de/cd98d4d86017a13ec4172ba3054e99.png)
Leetcode: Sword finger offer 66 Build product array [application of pre and post infix]

张驰课堂:2022年CAQ中质协六西格玛考试时间通知

Multithreading (V) -- concurrency tools (I) -- thread pool (II) -- related contents of ThreadPoolExecutor

leetcode:剑指 Offer 63. 股票的最大利润【记录前缀最小和 or 无脑线段树】
随机推荐
Meituan won the first place in fewclue in the small sample learning list! Prompt learning+ self training practice
Redis data structure (VIII) -- Geo
六月集训 第七日 ——哈希表
LeetCode-1350. Invalid students
SQL injection - blind injection
Video fire detection based on Gaussian mixture model and multi-color
Qt-- realize TCP communication
LeetCode-1303. Team size
It only takes 10 minutes to understand the underlying principle of NiO
SQL注入——联合查询union
LeetCode-1445. Apples and oranges
Flink practice
About session Getattribute, getattribute error
SQL注入原理即sqli-labs搭建,sql注入简单实战
LeetCode-1405. Longest happy string
LeetCode-1576. Replace all question marks
Idea common shortcut keys
SQL injection based on error reporting
六月集训 第八日——前缀和
Zhang Chi: is process a panacea?