LeetCode brush questions (7)

Math related problems

The greatest common factor and least common multiple of two numbers

思路
使用辗转相除法,The greatest common factor can be obtained（greatest common divisor,gcd）.将两个数相乘再除以最大公因数即可得到最小公倍数（least common multiple, lcm）.

int gcd(int a,int b){
    
	if(b==0)return a;
	return gcd(b,a%b);
}

int lcm(int a,int b){
    
	int g = gcd(a,b);
	return a*b/g;
}

204. Count Primes (Easy)

问题描述
给定一个数字n,求小于n 的质数的个数.

输入输出样例
示例 1：

输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 .

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：0

思路
思路1：最简单的方法,Determine whether a number is prime or not from scratch,是的话就计数.
思路2：Russian screening method,创建一个大小为n的数组,Set all positions to prime markers first.然后从2开始遍历,如果当前iposition is prime,就从i*i的位置开始,将所有iThe position of an integer multiple of is set as a composite number.When all elements are traversed in this way,There is a complete distinction between prime and composite numbers.Go through the statistics again.

代码1（超时）

class Solution {
    
    public int countPrimes(int n) {
    
        int count = 0;
        for(int i=0;i<n;i++){
    
            if(isPrimes(i))count++;
        }
        return count;
    }

    boolean isPrimes(int n){
    
        if(n == 1 || n==0)return false;
        for(int i=2;i<=n/2;i++){
    
            if(n%i == 0)return false;
        }
        return true;
    }
}

代码二（Russian screening method）

class Solution {
    
    public int countPrimes(int n) {
    
        boolean[] prime = new boolean[n];
        Arrays.fill(prime,true); //First mark all positions as prime numbers
        for(int i=2;i*i<n;i++){
     //遍历到sqrt(n)position can be filled,如果遍历到n后面int会溢出
            if(prime[i]){
    
                for(int j=i*i;j<n;j+=i){
     //关于为什么从i*i开始,Because the previous one has been filled with the previous number,No refill is required
                    prime[j]=false;
                }
            }
        }
        int count = 0;
        for(int i=2;i<n;i++){
    
            if(prime[i])count++;
        }
        return count;
    }
}

504. Base 7 (Easy)

问题描述
给定一个整数 num,将其转化为 7 进制,并以字符串形式输出.

输入输出样例

示例 1:

输入: num = 100
输出: “202”

示例 2:

输入: num = -7
输出: “-10”

思路
Hexadecimal conversion type questions,Usually division and modulo are used（mod）来进行计算,Also pay attention to some details,such as negative numbers and zeros.If the output is a number type instead of a string,Then you also need to consider whether the upper and lower bounds of the integer will be exceeded.【可作为Rbase template】

代码

class Solution {
    
    public String convertToBase7(int num) {
    
        if(num == 0)return "0";
        boolean is_negative = num<0;
        if(is_negative) num = -num; //If it is negative, it becomes first0
        String string = "";
        while (num!=0){
    
            int b = num%7;
            num = num/7;
            string = b+string;
        }
        if(is_negative)return "-"+string;
        return string;
    }
}

172. Factorial Trailing Zeroes

问题描述
给定一个整数 n ,返回 n! 结果中尾随零的数量.

提示 n! = n * (n - 1) * (n - 2) * … * 3 * 2 * 1

输入输出样例

示例 1：

输入：n = 3
输出：0
解释：3! = 6 ,不含尾随 0

示例 2：

输入：n = 5
输出：1
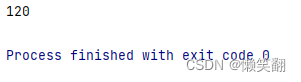
解释：5! = 120 ,有一个尾随 0

思路
每个尾部的0 由2 × 5 = 10 而来,因此我们可以把阶乘的每一个元素拆成质数相乘,统计有
多少个2 和5.明显的,质因子2 的数量远多于质因子5 的数量,因此我们可以只统计阶乘结果里有多少个质因子5.

代码

class Solution {
    
    public int trailingZeroes(int n) {
    
        int count = 0;
        for(int i=5;i<=n;i+=5){
    
            int j = i;
            while (j%5 == 0){
    
                count++;
                j/=5;
            }
        }
        return count;
    }
}

代码二

class Solution {
    
    public int trailingZeroes(int n) {
    
        if (n==0) return 0;
        return n/5+trailingZeroes(n/5);
    }
}

415. Add Strings (Easy)

问题描述

给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回.
你不能使用任何內建的用于处理大整数的库（比如 BigInteger）, 也不能直接将输入的字符串转换为整数形式.

输入输出样例

示例 1：

输入：num1 = “11”, num2 = “123”
输出：“134”

示例 2：

输入：num1 = “456”, num2 = “77”
输出：“533”

思路
Use two pointers to point to the end of the two strings respectively,Then use the vertical addition method to add the numbers pointed to by the two pointers.注意一种情况：99999+1,To keep going.If a character is shorter,It can be zero-padded in front.

代码

class Solution {
    
    public String addStrings(String num1, String num2) {
    
        int m = num1.length();
        int n = num2.length();
        int i = m-1,j = n-1;
        int pre = 0;//进位
        int sum = 0;//两数之和
        StringBuilder stringBuilder = new StringBuilder();
        while (i>=0 || j>=0 || pre!=0){
     //when all digits are used up,But both are zero-padded when the carry is not zero
            int a = i>=0?num1.charAt(i)-'0' : 0; //Not enough digits to fill
            int b = j>=0?num2.charAt(j)-'0' : 0;
            sum = a+b+pre; //Add two numbers and add the carry flag
            pre = (a+b+pre)/10; //更新进位
            stringBuilder.append(sum%10);
            i--;j--;
        }
        return stringBuilder.reverse().toString();
    }
}

326. Power of Three (Easy)

问题描述
给定一个整数,写一个函数来判断它是否是 3 的幂次方.如果是,返回 true ;否则,返回 false .

整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

示例 1：

输入：n = 27
输出：true

示例 2：

输入：n = 0
输出：false

思路
可以一直用3除n,如果不满足n%3==0,则返回false.

代码

class Solution {
    
    public boolean isPowerOfThree(int n) {
    
        if(n == 0)return false;
        if(n == 1)return true;
        if(n%3 != 0)return false;
        return isPowerOfThree(n/3);
    }
}

class Solution {
    
    public boolean isPowerOfThree(int n) {
    
        if(n == 0)return false;
        while (n%3==0){
    
            n = n/3;
        }
        if(n == 1)return true;
        return false;
    }
}

代码二

class Solution {
    
    public boolean isPowerOfThree(int n) {
    
        if(n>0) return 1162261467%n == 0; //int范围内,3The maximum power of 1162261467,If divisible by this number,则n是3的次幂
        return false;
    }
}

384. Shuffle an Array (Medium)

问题描述
The input is an array of integer numbers,and an array containing the instruction function names.输出是一个二维数组,
Represents an array generated by each instruction.

输入输出样例
Input: nums = [1,2,3], actions: [“shuffle”,“shuffle”,“reset”]
Output: [[2,1,3],[3,2,1],[1,2,3]]
在这个样例中,The results of the first two scrambles can only be randomly generated.

思路
我们采用经典的Fisher-Yates 洗牌算法,原理是通过随机交换位置来实现随机打乱,有正向
和反向两种写法,且实现非常方便.注意这里“reset”Implementation details of functions and constructors of classes.

代码

class Solution {
    
    int[] nums;
    public Solution(int[] nums) {
    
        this.nums = nums;
    }

    public int[] reset() {
    
        return this.nums;
    }

    public int[] shuffle() {
    
        int n = nums.length;
        int[] new_nums = Arrays.copyOf(nums,nums.length);
        for(int i=0;i<n;i++){
    
            int rand = (int)(Math.random()*n); //Math.random产生[0,1)范围的随机数
            swap(new_nums,i,rand);
        }
        return new_nums;
    }
    private void swap(int[] nums,int a,int b){
    
        int tem = nums[a];
        nums[a] = nums[b];
        nums[b] = tem;
    }
}

/** * Your Solution object will be instantiated and called as such: * Solution obj = new Solution(nums); * int[] param_1 = obj.reset(); * int[] param_2 = obj.shuffle(); */

528. Random Pick with Weight (Medium)

问题描述
给你一个 下标从 0 开始 的正整数数组 w ,其中 w[i] 代表第 i 个下标的权重.

请你实现一个函数 pickIndex ,它可以 随机地 从范围 [0, w.length - 1] 内（含 0 和 w.length - 1）选出并返回一个下标.选取下标 i 的 概率 为 w[i] / sum(w) .

例如,对于 w = [1, 3],挑选下标 0 的概率为 1 / (1 + 3) = 0.25 （即,25%）,而选取下标 1 的概率为 3 / (1 + 3) = 0.75（即,75%）.

输入输出样例
示例 1：

输入：
[“Solution”,“pickIndex”]
[[[1]],[]]
输出：
[null,0]
解释：
Solution solution = new Solution([1]);
solution.pickIndex(); // 返回 0,因为数组中只有一个元素,所以唯一的选择是返回下标 0.

思路
假设一个数组为【2,3,5】,Its prefix sum array is 【2,5,10】.随机产生一个0-9的数字,如果是[0 1]返回前缀0,[ 2 3 4]返回前缀1,[5,6,7,8,9]返回前缀2.It is equivalent to a number with a large weight,Map a large range number to the region when random.The way to map is：Returns the sum of the first greater than the arrayrand的索引.

代码

class Solution {
    

    int[] sum_nums;
    public Solution(int[] w) {
    
        sum_nums = new int[w.length];
        sum_nums[0]=w[0];
        for(int i=1;i<w.length;i++){
    
            sum_nums[i]=sum_nums[i-1]+w[i];
        }
    }

    public int pickIndex() {
    
        int b = sum_nums[sum_nums.length-1];
        int rand = (int)(Math.random()*b);
        return search(sum_nums,rand);
    }
    public int search(int[] sum,int t){
    
        int low=0;
        int high = sum.length-1;
        while (low<=high){
    
            int mid = low + (high-low)/2;
            if(sum[mid]==t)return mid+1;
            else if(sum[mid]>t) high = mid-1;
            else low = mid+1;
        }
        return low; //When searching for nonexistent numbers,结束后tartget在nums[high]和nums[low]之间
    }
}

382. Linked List Random Node (Medium)

问题描述
给你一个单链表,随机选择链表的一个节点,并返回相应的节点值.每个节点 被选中的概率一样 .

实现 Solution 类：

Solution(ListNode head) 使用整数数组初始化对象.
int getRandom() 从链表中随机选择一个节点并返回该节点的值.链表中所有节点被选中的概率相等.

思路
先遍历一遍链表,求链表长度len.Then randomly generate one[0,len)范围的随机数rand,Then the pointer goes backwardsrand步.
【Reservoir sampling method：Convert space consumption to time consumption（Personal feelings and ideas are worth learning from,But the efficiency is not as good as the previous idea.后面有时间再学）】

class Solution {
    

    int len = 0;
    ListNode head;
    public Solution(ListNode head) {
    
        this.head = head;
        ListNode p = head;
        while(p!=null){
    
            len++;
            p = p.next;
        }
    }

    public int getRandom() {
    
        Random random = new Random();
        int rand = random.nextInt(len);
        ListNode p = head;
        for(int i=0;i<rand;i++){
    
            p = p.next;
        }
        return p.val;
    }
}

168. Excel Sheet Column Title (Easy)

问题描述
给你一个整数 columnNumber ,返回它在 Excel 表中相对应的列名称.

例如：

A -> 1
B -> 2
C -> 3
…
Z -> 26
AA -> 27
AB -> 28
…

输入输出样例
示例 1：

输入：columnNumber = 1
输出：“A”
示例 2：

输入：columnNumber = 28
输出：“AB”

思路
One thing to note is from1 开始而不是0.So you can convert numbers-1变为从0开始计数,再将其转换为26进制表示.

class Solution {
    
    public String convertToTitle(int columnNumber) {
    
        StringBuilder stringBuilder = new StringBuilder();
        int a = 0;
        while (columnNumber>0){
    
            columnNumber-=1; //Change the number to from0开始计数
            a = columnNumber%26;
            stringBuilder.append(Character.toChars('A'+a));
            columnNumber/=26;
        }
        return stringBuilder.reverse().toString();
    }
}

67. Add Binary (Easy)

问题描述
给你两个二进制字符串,返回它们的和（用二进制表示）.
输入为 非空 字符串且只包含数字 1 和 0.

输入输出样例
示例 1:

输入: a = “11”, b = “1”
输出: “100”

示例 2:

输入: a = “1010”, b = “1011”
输出: “10101”

思路
The same idea as the previous decimal addition and summation.

代码

class Solution {
    
    public String addBinary(String a, String b) {
    
        int m=a.length();
        int n=b.length();
        int i=m-1,j=n-1;
        int pre = 0;
        StringBuilder stringBuilder = new StringBuilder();
        while (i>=0 || j>=0 || pre>0){
    
            int num1 = i>=0?a.charAt(i)-'0':0;
            int num2 = j>=0?b.charAt(j)-'0':0;
            int sum = num1+num2+pre;
            stringBuilder.append(sum%2);
            pre = sum/2;
            i--;j--;
        }
        return stringBuilder.reverse().toString();
    }
}

238. Product of Array Except Self (Medium)

问题说明
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 .

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内.

请不要使用除法,且在 O(n) 时间复杂度内完成此题.

输入输出样例

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

思路
用一个L数组,L[i]表示iThe product of the left-hand numbers;用一个R数组,R[i]Represents the product of the numbers on the right;则输出数组out[i]=L[i]*R[i]

代码

class Solution {
    
    public int[] productExceptSelf(int[] nums) {
    
        int n = nums.length;
        int[] L = new int[n];
        int[] R = new int[n];
        L[0]=1;
        for(int i=1;i<n;i++){
     //L[i]表示iThe product of the numbers on the left
            L[i]=L[i-1]*nums[i-1];
        }
        R[n-1]=1;
        for(int i=n-2;i>=0;i--){
    //R[i]表示iThe product of the numbers on the right
            R[i]=R[i+1]*nums[i+1];
        }
        for(int i=0;i<n;i++){
    
            nums[i]=L[i]*R[i];
        }
        return nums;
    }
}

462. Minimum Moves to Equal Array Elements II (Medium)

问题描述
给你一个长度为 n 的整数数组 nums ,返回使所有数组元素相等需要的最少移动数.

在一步操作中,你可以使数组中的一个元素加 1 或者减 1 .

输入输出样例

示例 1：

输入：nums = [1,2,3]
输出：2
解释：
只需要两步操作（每步操作指南使一个元素加 1 或减 1）：
[1,2,3] => [2,2,3] => [2,2,2]

示例 2：

输入：nums = [1,10,2,9]
输出：16

思路
Moving the fewest steps requires moving all values ​​to the median value.If the array is odd,Just the median.如果数组是偶数,The median is rounded up or down（Both ways move the same number of steps）.

代码

class Solution {
    
    public int minMoves2(int[] nums) {
    
        Arrays.sort(nums);
        int n = nums.length;
        int mid = nums[n/2];
        int sum = 0;
        for(int i=0;i<n;i++){
    
            sum += Math.abs(nums[i]-mid);
        }
        return sum;
    }
}

169. Majority Element (Easy)

问题描述
给定一个大小为 n 的数组 nums ,返回其中的多数元素.多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素.

你可以假设数组是非空的,并且给定的数组总是存在多数元素.

输入输出样例

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

思路
Choose a target faction,People from the same camp join,People from different camps cancel each other out.Re-select a target faction when the number is zero,The last remaining person is the target camp.
从第一个数开始count=1,遇到相同的就加1,遇到不同的就减1,减到0就重新换个数开始计数,总能找到最多的那个.

代码

class Solution {
    
    public int majorityElement(int[] nums) {
    
        int count = 0;
        int target = nums[0];
        for(int i=0;i<nums.length;i++){
    
            if(nums[i]==target){
    
                count++;
            }else count--;
            if(count==0) target = nums[i+1];
        }
        return target;
    }
}

470. Implement Rand10() Using Rand7() (Medium)

问题描述
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数.

你只能调用 rand7() 且不能调用其他方法.请不要使用系统的 Math.random() 方法.

每个测试用例将有一个内部参数 n,即你实现的函数 rand10() 在测试时将被调用的次数.请注意,这不是传递给 rand10() 的参数.

输入输出样例
示例 1:

输入: 1
输出: [2]

示例 2:

输入: 2
输出: [2,8]

思路
参考思路
This question can be expanded into a class of questions,即使用randN()产生randM()的随机数.假设M大于N.
利用randN()产生randM()There is a rule,即：(rand_N()-1)*R+rand_R()可以产生1~NRuniform random number.
反之利用randM()产生randN()存在：rand_M()%N+1可以产生1-Nuniform random number（其中M是N的整数倍）

针对本问题,Consider generating one first1-49uniform random number.但考虑到49不是10的整数倍,You can choose to discard a portion.使用1-40的随机数生成1-10的随机数.

代码

/** * The rand7() API is already defined in the parent class SolBase. * public int rand7(); * @return a random integer in the range 1 to 7 */
class Solution extends SolBase {
    
    public int rand10() {
    
        while (true){
    
            int a = rand7(); 
            int b = rand7();
            int rand = (a-1)*7+b; //产生1-49Uniform random numbers
            if(rand<=40) return rand%10+1; //rand%10产生0-9的随机数
        }
    }
}

优化
In order to reduce the probability of unqualified loop sampling,Optimize by re-filtering the samples with ineligible conditions：

class Solution extends SolBase {
    
    public int rand10() {
    
        while (true){
    
            int a = rand7(); 
            int b = rand7();
            int rand = (a-1)*7+b; //产生1-49Uniform random numbers
            if(rand<=40) return rand%10+1; //rand%10产生0-9的随机数

            a = rand-40; //rand9
            b = rand7();
            rand = (a-1)*7+b; //产生1-63Uniform random numbers
            if(rand<=60) return rand%10+1;//rand%10产生0-9的随机数

            a = rand-60; //rand3
            b = rand7();
            rand = (a-1)*7 +b ;//产生1-21的随机数
            if(rand<=20) return rand%10+1;//rand%10产生0-9的随机数
        }
    }
}

202. Happy Number (Easy)

问题描述
编写一个算法来判断一个数 n 是不是快乐数.

「快乐数」 定义为：

对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和.
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1.
如果这个过程 结果为 1,那么这个数就是快乐数.
如果 n 是 快乐数 就返回 true ;不是,则返回 false .

输入输出样例
示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

思路
对于一个数n,If it is a happy number, after a certain number of cycles, the sum of the squares of the digits is 1;如果不是快乐数,The sum of the squares of its individual digits is repeated in a loop.于是我们可以用一个HashsetSave the sum of the squares of each number,If it appears againHashSetIt shows that it is not a happy number.

代码

class Solution {
    
    public boolean isHappy(int n) {
    
        Set<Integer> set = new HashSet<>();
        while (true){
    
            int s = 0;
            while (n>0){
    
                int a = n%10; //当前位数
                s += a*a;
                n /= 10;
            }
            if(s == 1)return true;
            if(set.contains(s))return false;
            set.add(s);
            n = s;
        }
    }
}