李航《统计学习方法》笔记之感知机perceptron

感知机(perceptron)

2.1 介绍

感知机(perceptron)是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式。感知机预测是用学习得到的感知机模型对新的输入实例进行分类。感知机1957年由Rosenblatt提出，是神经网络与支持向量机的基础。

结构为介绍感知机模型，感知机的学习策略，特别是损失函数，介绍感知机学习算法，包括原始形式和对偶形式，并证明算法的收敛性。

2.1.2总结summarization

1.一条直线不分错一个点,这就是好的直线。
2.模型要尽可能找到好的直线。
3.如果没有好的直线，在差的直线中找到较好的直线。
4.判断直线多差的方式:分错的点到直线的距离求和，距离越大则模型越差。

2.2 定义

(感知机) 假设输入空间（特征空间) 是 $\mathcal{X} \subseteq \mathbf{R}^{n} $, 输出空间是 $ \mathcal{Y}={+1,-1}$ 。输入 $ x \in \mathcal{X}$ 表示实例的特征向量, 对应于输入空间（特征空间）的点; 输出 $ y \in \mathcal{Y} $ 表示实例的类别。由输入空间到输出空间的如下函数:

KaTeX parse error: {align} can be used only in display mode.

称为感知机。其中, w 和 b 为感知机模型参数, $w\in {\mathbf{R}}^n$ 叫作权值 ( weight) 或权值向量 (weight vector), $b \in \mathbf{R} $ 叫作偏置 ( bias), $ w \cdot x $表示 w 和 x 的内积。 $\operatorname{sign} $是符号函数, 即

KaTeX parse error: {align} can be used only in display mode.

感知机是一种线性分类模型, 属于判别模型。感知机模型的假设空间是定义在 特征空间中的所有线性分类模型（linear classification model）或线性分类器（linear classifier）, 即函数集合$ {f \mid f(x)=w \cdot x+b} $。

感知机有如下几何解释: 线性方程

$w\cdot x+b=0$

2.3 参数说明

对应于特征空间 ${\mathbf{R}}^n$ 中的一个超平面 S , 其中w 是超平面的法向量, b 是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点 (特征向量) 分别被分为正、负两类。

特征空间也就是整个n维空间，样本的每个属性都叫一个特征，特征空间的意思是在这个空间中可以找到样本所有的属性组合。

因此, 超平面 S 称为分离超平面 (separating hyperplane), 如下图所示。

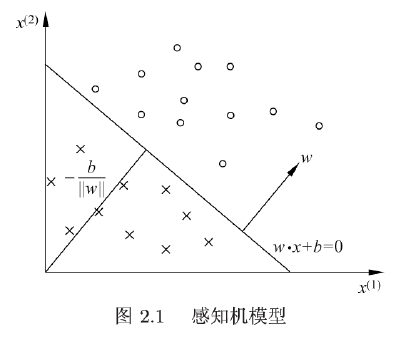
感知机学习, 由训练数据集 (实例的特征向量及类别)

$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$

其中, $ x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_{i} \in \mathcal{Y}={+1,-1}, i=1,2, \cdots, N $, 求得感知机模型, 即求得模型参数 w, b 。感知机预测, 通过学习得到的感知机模型, 对于新的输入实例给出其对应的输出类别。

2.4 可分和不可分数据集

对比线性可分和线性不可分的数据集：

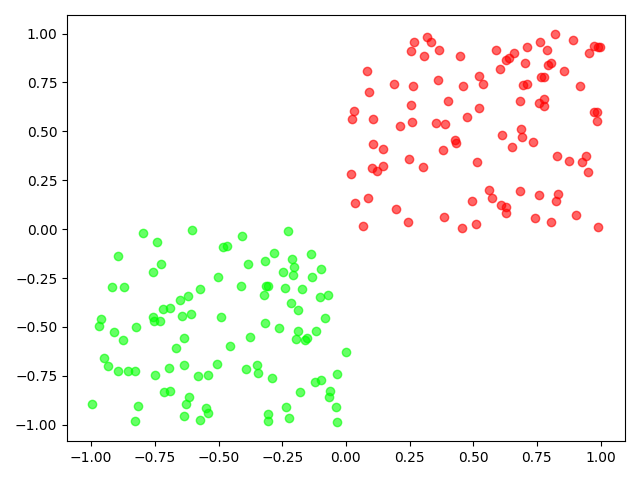
严格定义：

定义 2.2 (数据集的线性可分性) 给定一个数据集

$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$

其中, $ x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_{i} \in \mathcal{Y}={+1,-1}, i=1,2, \cdots, N $, 如果存在某个超平面 S

$w\cdot x+b=0$

能将数据集的正实例点和负实例点完全正确地划分到超平面的两侧, 即对所有 $ y_{i}=+1$ 的实例 i , 有 $w \cdot x_{i}+b>0 $, 对所有 $ y_{i}=-1 $ 的实例 i , 有 $ w \cdot x_{i}+b<0 $, 则称数据集 T 为线性可分数据集 (linearly separable data set),否则,称数据集 T 线性不可分。

2.5 感知机的学习策略（Learning policy）

函数间隔与几何间隔
空间中任意一个点 $x_{0} $ 到超平面$ \mathrm{S}$ 的距离：

2.5.1 函数间距

$\left|w\cdot x_0+b\right|$

函数间距并不常使用，因为等比例的扩大或者缩小w和b将使得超平面不变的情况下其距离可以调整，并不能很好地用于比较。

2.5.2 几何间距

$\frac{1}{\Vert w\Vert }\left|w\cdot x_0+b\right|$ 其中$\Vert w{\Vert }_2$为$w$的$L_2范数$$ \quad|w|{2}=\sqrt{\sum{i=1}^{N} w_{i}^{2}}$

而在几何间距中可以很好地解决这个问题：等比例地扩缩w和b，通过L2范数地变化可以抵消。因此几何间距常用。

2.5.3 感知机的学习算法——原始形式

对于误分类数据而言,

$-y_i\left(w\cdot x_i+b\right)>0$

误分类点 $ x_{i} $ 到超平面 $\mathrm{S} $ 的距离为：(绝对值可以去掉)

$-\frac{1}{\Vert w\Vert }{y}_i\left(w\cdot x_i+b\right)$

因此，所有误分类点（集合M）到超平面 S 的总距离为：

$-\frac{1}{\Vert w\Vert }{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$

损失函数

$L(w,b)=-{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$

2.5.4 原始形式算法过程

1.任选取超平面 $ w_{0}, b_{0}$ (做一个初始化)

2.采用梯度下降法极小化目标函数

$\begin{array}{l}L(w,b)=-{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)\\ {\nabla }_{w}L(w,b)=-{\sum }_{x_i\in M}{y}_i{x}_i\\ {\nabla }_{b}L(w,b)=-{\sum }_{x_i\in M}{y}_i\end{array}$

这里采用了函数间隔，因为感知机是误分类驱动，最终的目标是没有一个分错的样本（线性可分数据集），因此最后理想为0，这时放缩参数不影响。当然也可以用几何间隔。

3.更新 w, b

由$x_2=x_1-f^{\prime }(x_1)\eta$，可知

$\begin{array}{l}w\leftarrow w+\eta y_i{x}_i\\ b\leftarrow b+\eta y_i\end{array}$

注意，上面是对单点更新，每一个点走一步更新一次。若换成以下形式，则是对所有误分类的样本更新一次。

$\begin{array}{l}w\leftarrow w+{\sum }_{x_i\in M}{y}_i{x}_i\\ b\leftarrow b+{\sum }_{x_i\in M}{y}_i\end{array}$

2.5.5 例题

例 2.1 如图所示的训练数据集, 其正实例点是 $ x_{1}=(3,3)^{\mathrm{T}}, x_{2}=(4,3)^{\mathrm{T}} $, 负实例点是 $ x_{3}=(1,1)^{\mathrm{T}}$ , 试用感知机学习算法的原始形式求感知机模型 $f(x)= \operatorname{sign}(w \cdot x+b) $ 。这里, $w=\left(w^{(1)}, w^{(2)}\right){\mathrm{T}}, x=\left(x^{(1)}, x^{(2)}\right){\mathrm{T}} $。

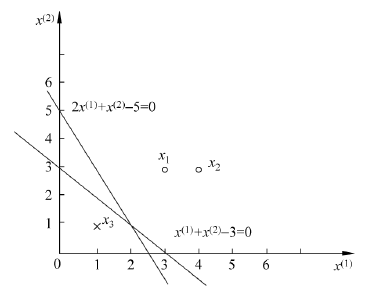
1.构建损失函数

$\min L(w,b)=-{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$

2.梯度下降求解 w, b 。设步长为 1

• 取初值 $w_{0}=0, b_{0}=0 $

• 对于 $ x_{1}, y_{1}\left(w_{0} \cdot x_{1}+b_{0}\right)=0$ 末被正确分类，更新 w, b 。

  $w_1=w_0+x_1{y}_1=(3,3{)}^T,b_1=b_0+y_1=1*w_1\cdot x+b_1=3x^{(1)}+3x^{(2)}+1$

3. 对 $x_{1}, x_{2} $ ，显然 $y_{i}\left(w_{1} \cdot x_{i}+b_{1}\right)>0 $ ，被正确分类，不作修改。对于 $ x_{3}, y_{3}\left(w_{1}\right. . \left.x_{3}+b_{1}\right)<0 $，被误分类，更新$ w ， b$。

   $w_2=w_1+x_3{y}_3=(2,2{)}^T,b_2=b_1+y_3=0*w_2\cdot x+b_2=2x^{(1)}+2x^{(2)}$

4. 以此往复，直到没有误分类点，损失函数达到极小。

这是在计算中误分类点先后取 $ x_{1}, x_{3}, x_{3}, x_{3}, x_{1}, x_{3}, x_{3} $ 得到的分离超平面和感知机模型。如果在计算中误分类点依次取 $x_{1}, x_{3}, x_{3}, x_{3}, x_{2}, x_{3}, x_{3}, x_{3}, x_{1}, x_{3}, x_{3} $ 那么得到的分离超平面是 $ 2 x^{(1)}+x{(2)}-5=0 $ 。
感知机学习算法由于采用不同的初值或选取不同的误分类点, 解可以不同。