The number of nodes of a complete binary tree [non-O (n) solution ＞ Abstract dichotomy]

Preface

Abstract dichotomy is everywhere , To quickly cut down half the useless data , This reduces the time complexity .
Abstract the rules of dichotomy , Then bisection can be flexibly applied to a variety of scenarios .
With O(logN * logN) < O(N) To find the number of nodes of a complete binary tree .

One 、 The number of nodes in a complete binary tree

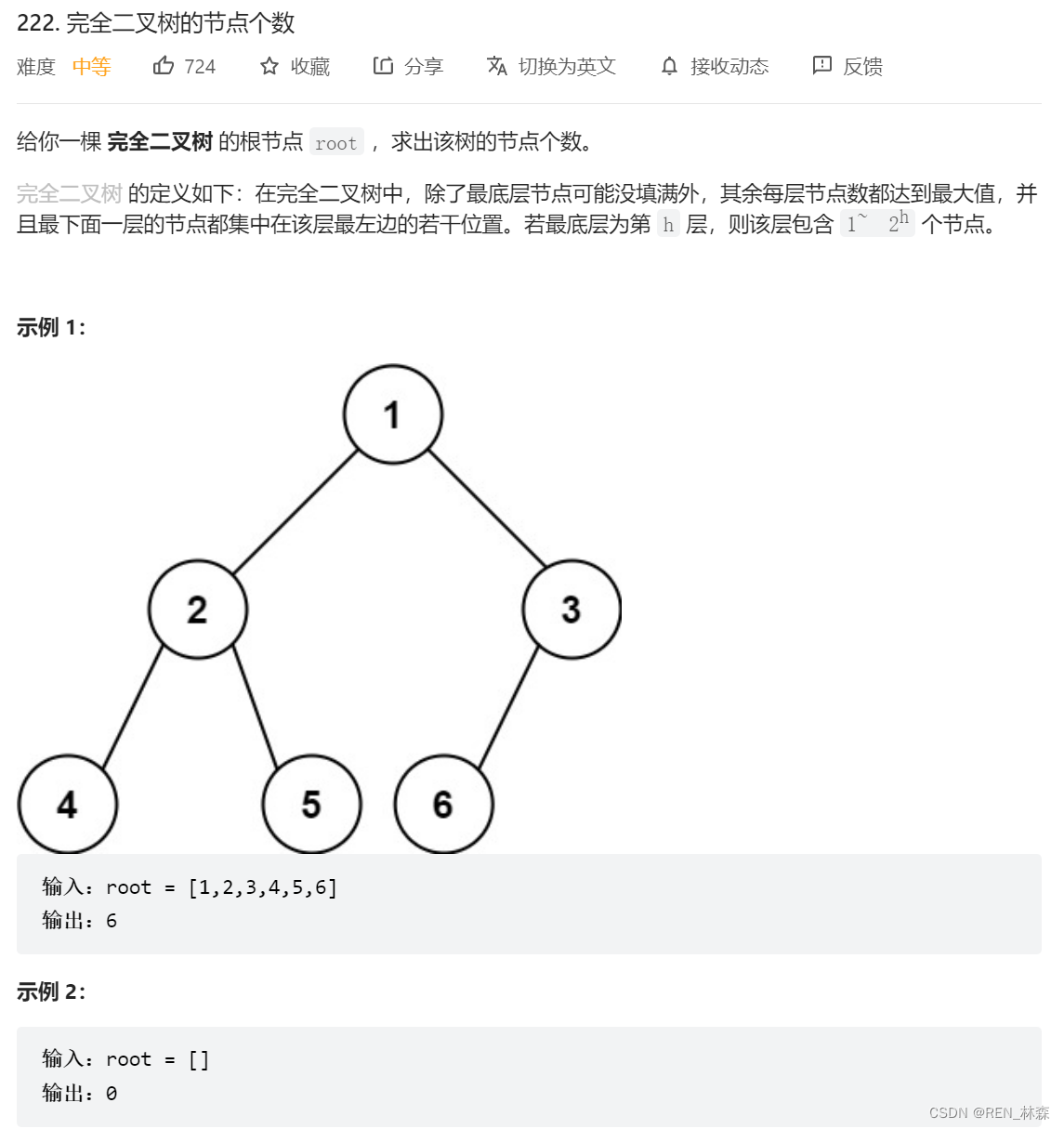
Two 、 Abstract dichotomy

package everyday.medium;

//  The number of nodes in a complete binary tree .
public class CountNodes {
    
    /* target： Find the number of complete binary tree nodes ,  At most one level of a complete binary tree is not full ; If the last floor is not full , There are also nodes from left to right , And each sub tree has left children first and then right children .  key problem ： Find the last node of the last layer .  Every time a leaf node is found logN, Find in two logN, So time complexity O(logN * logN) < O(N), because O(logN) < O(sqrt(N)) */
    public int countNodes(TreeNode root) {
    
        if (root == null) return 0;
        //  Determine tree height .
        int hLeft = getLevel(root);
        //  Two points 
        // int width = (int) Math.pow(2, hLeft - 1);
        //  Read other people's comments , in the light of 2 To what power , Can be replaced by bit operation .
        int width = 1 << hLeft - 1;
        int low = 0, high = width - 1;
        while (low < high) {
    
        	//  coordination low = mid, Prevent a dead cycle .
            int mid = low + (high - low + 1 >>> 1);

            int level = hLeft;
            int sum = 0;
            TreeNode p = root;
            while (level-- > 1) {
    
                if ((sum + (1 << level - 1)) > mid) p = p.left;
                else {
    
                    sum += 1 << level - 1;
                    p = p.right;
                }
            }
            //  Find the last node .
            if (p == null) high = mid - 1;
            else low = mid;
        }
        //  Calculate the total number of nodes . Remove the number of nodes in the last layer  +  Number of nodes in the last layer 
        return (int) ((1 << hLeft - 1) - 1) + (low + 1);
    }

    //  Determine the left depth of the tree .
    private int getLevel(TreeNode root) {
    
        int h = 0;
        while (root != null) {
    
            ++h;
            root = root.left;
        }
        return h;
    }

    // Definition for a binary tree node.
    public class TreeNode {
    
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
    
        }

        TreeNode(int val) {
    
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
    
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

}

summary

1） Perfect binary tree .
2） With O(logN * logN) To get the number of nodes of a complete binary tree .
3） Abstract dichotomy + How to use O(logN) Find the second of the complete binary tree N A leaf node .

reference

[1] LeetCode The number of nodes in a complete binary tree