当前位置:网站首页>信息学奥赛一本通 1362:家庭问题(family)
信息学奥赛一本通 1362:家庭问题(family)
2022-06-30 19:48:00 【君义_noip】
【题目链接】
【题目考点】
1. 图论 图的遍历
3. 并查集
【解题思路】
本题按照原意直接理解当然也能做。如果用图论这一数据结构来辅助理解,结合图论中的定义,可以理解到这个问题的本质。
每个人是一个顶点,任何人之间的关系是边,所有的人和关系构成一个图,一个家庭就是一个连通分量。
求家庭个数就是求连通分量的个数,最大家庭人数就是所有连通分量中顶点数量最多的连通分量的顶点数。
可以在图上用搜索(深搜/广搜)来确定连通分量的数量。也可以使用并查集来完成。
(连通块本质上也是图上的连通分量,该题做法和求连通块问题类似)
解法1:搜索
从每个顶点尝试开始搜索,如果成功开始进行一次搜索,即可标记整个连通分量。成功开始搜索的次数即为连通分量的个数。搜索过程中对这一趟搜索到的顶点做计数,能达到在最大计数即为顶点数量最多的连通分量的顶点数。
解法2:并查集
将有关系的人加入一个集合。如果i与j有关系,那么把i所在的集合与j所在的集合合并,合并后的集合的元素个数为原来两集合元素个数的加和。最后统计集合数量,以及查找得到元素个数最大的集合的元素个数。
【题解代码】
解法1:搜索
- 深搜+邻接表
#include <bits/stdc++.h>
using namespace std;
#define N 105
vector<int> edge[N];//邻接表
int n, m, num, mx, ct;//num:连通分量数 ct:当前连通分量中的顶点数 mx:最大顶点数
bool vis[N];//vis[i]:顶点i是否已访问过
void init()//生成图
{
int f, t;
cin >> n >> m;
for(int i = 1; i <= m; ++i)
{
cin >> f >> t;
edge[f].push_back(t);
edge[t].push_back(f);
}
}
void dfs(int u)
{
for(int i = 0; i < edge[u].size(); ++i)
{
int v = edge[u][i];
if(vis[v] == false)
{
ct++;
vis[v] = true;
dfs(v);
}
}
}
int main()
{
init();
for(int i = 1; i <= n; ++i)
{
if(vis[i] == false)
{
num++;
ct = 1;
vis[i] = true;
dfs(i);
mx = max(mx, ct);//更新最大顶点数
}
}
cout << num << ' ' << mx;
return 0;
}
- 广搜+邻接矩阵
#include <bits/stdc++.h>
using namespace std;
#define N 105
bool edge[N][N];//邻接矩阵
int n, m, num, mx, ct;//num:连通分量数 ct:当前连通分量中的顶点数 mx:最大顶点数
bool vis[N];//vis[i]:顶点i是否已访问过
void init()
{
int f, t;
cin >> n >> m;
for(int i = 1; i <= m; ++i)
{
cin >> f >> t;
edge[f][t] = edge[t][f] = true;
}
}
void bfs(int v)//从顶点v开始广搜
{
queue<int> que;
vis[v] = true;
ct++;
que.push(v);
while(que.empty() == false)
{
int u = que.front();
que.pop();
for(int i = 1; i <= n; ++i)
{
if(edge[u][i] && vis[i] == false)
{
ct++;
vis[i] = true;
que.push(i);
}
}
}
}
int main()
{
init();
for(int i = 1; i <= n; ++i)
{
if(vis[i] == false)
{
num++;
ct = 0;
bfs(i);
mx = max(mx, ct);//更新最大顶点数
}
}
cout << num << ' ' << mx;
return 0;
}
3. 并查集
#include<bits/stdc++.h>
using namespace std;
#define N 105
int fa[N], n, m;
int ct[N];//ct[i]:以i为根结点的树的结点数量
void init(int n)
{
for(int i = 1; i <= n; ++i)
{
fa[i] = i;
ct[i] = 1;
}
}
int find(int x)
{
if(x == fa[x])
return x;
else
return fa[x] = find(fa[x]);
}
void merge(int i, int j)//合并i结点和j结点所在的集合
{
int x = find(i), y = find(j);
fa[x] = y;//x的父结点设为y
if(x != y)
ct[y] += ct[x];//以y为根节点的集合的顶点数ct[y]增加ct[x]
}
int main()
{
int f, t, num = 0, mx = 0;
cin >> n >> m;
init(n);
while(m--)
{
cin >> f >> t;
merge(f, t);
}
for(int i = 1; i <= n; ++i)
{
if(find(i) == i)//i是根结点
{
num++;//根结点的数量即为集合的数量
mx = max(ct[i], mx);//更新集合元素数量的最大值
}
}
cout << num << ' ' << mx;
return 0;
}
边栏推荐
猜你喜欢

CV+Deep Learning——网络架构Pytorch复现系列——basenets(BackBones)(一)

建立自己的网站(20)

企业中台规划和IT架构微服务转型

Detailed explanation of specific methods and steps for TCP communication between s7-1500 PLCs (picture and text)

CADD课程学习(1)-- 药物设计基础知识

Idle fish is hard to turn over

MySQL billing Statistics (Part 1): MySQL installation and client dbeaver connection
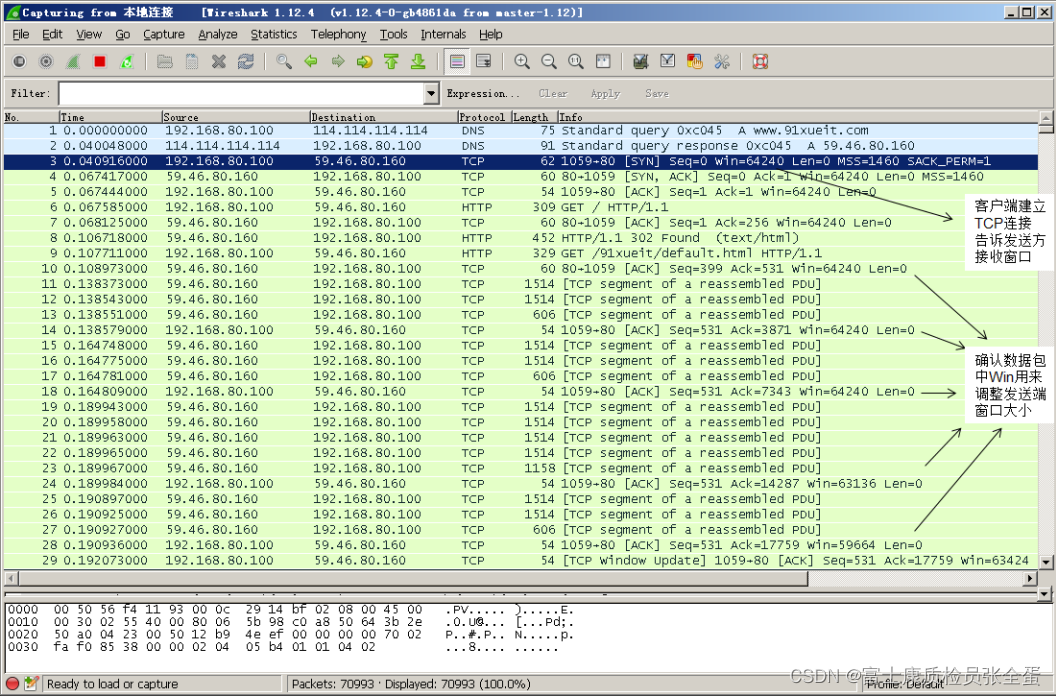
Transport layer uses sliding window to realize flow control

Enterprise middle office planning and it architecture microservice transformation

MySQL master-slave synchronization
随机推荐
Primary school, session 3 - afternoon: Web_ sessionlfi
Torchdrug -- drug attribute prediction
[iccv 2019] characteristics precise supervision of feature super resolution for small object detection
Why should offline stores do new retail?
WeakSet
数据智能——DTCC2022!中国数据库技术大会即将开幕
QT :QAxObject操作Excel
qt中toLocal8Bit和toUtf8()有什么区别
PS2手柄-1「建议收藏」
《微信小程序-基础篇》带你了解小程序中的生命周期(二)
CADD课程学习(1)-- 药物设计基础知识
【Try to Hack】Windows系统账户安全
Tensorflow2.4实现RepVGG
1. 爬虫之Beautifulsoup解析库&在线解析图片验证码
启动PHP报错ERROR: [pool www] cannot get uid for user ‘@[email protected]’
RP prototype resource sharing - shopping app
毕业季职场人
派尔特医疗在港交所招股书二次“失效”,上市计划实质性延迟
neo4j load csv 配置和使用
MySQL数据库查询优化