当前位置:网站首页>最小割和对偶图(未完成)
最小割和对偶图(未完成)
2022-08-02 12:49:00 【C_eeking】
算法思想
最小割
最小割与最大流在大部分情况下是等价的,一般来说,求解最小割就是求解最大流,但是对于许多模型来说(例如网格图),由于建图的点和边过多,在建图的基础上再采用最大流算法,会加大时间复杂度和空间复杂度,这个时候如果利用平面图转对偶图的性质,那么原图的空间复杂度惠减少,在此基础上选择图论中更恰当的算法能够减小时间复杂度
其余具体概念和连续可以参考另一篇最大流最小割
对偶图
训练
LuoguP4001
题目大意:略
思路:本题可以用最小割或者对偶图最短路来处理
如果把左上角视为起点,右下角视为重点,那么原题目的封锁就可以认为是在图上找一个如图所示的最小割(虚线经过的边),因此直接建图然后跑最大流即可,但是需要优化后的DInic算法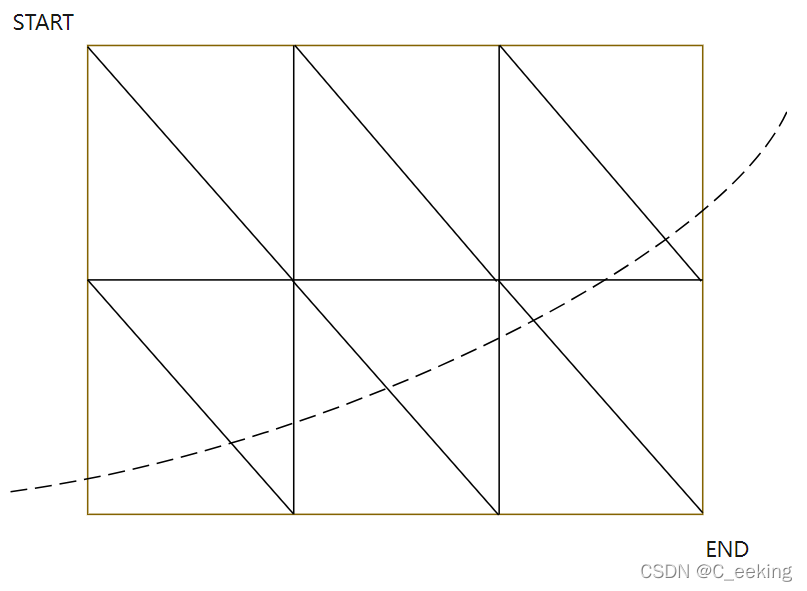 如果选择对偶图+最短路,需要将图的最外平面分成两个,然后分别建边,左下角为起点,右上角为终点,跑最短路即可
如果选择对偶图+最短路,需要将图的最外平面分成两个,然后分别建边,左下角为起点,右上角为终点,跑最短路即可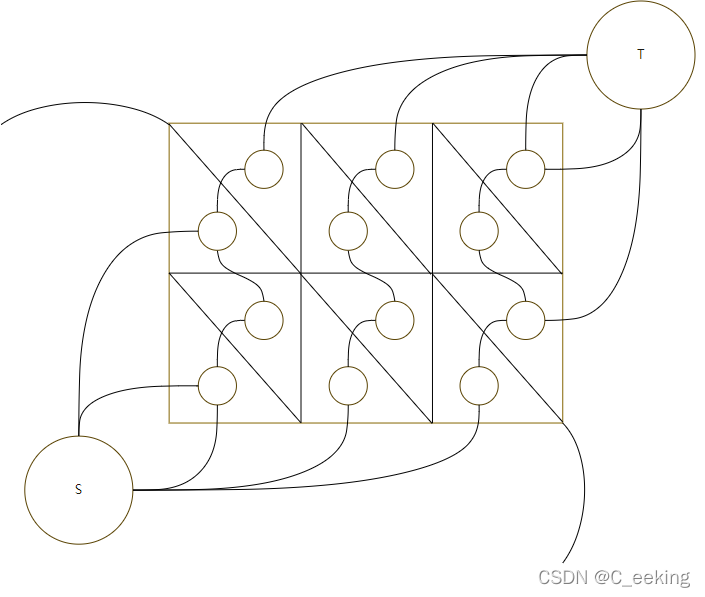
代码(最大流最小割)
#include <bits/stdc++.h>
//#define int long long//不要开long long,会超内存,要么就超时
const int inf=0x3f3f3f3f;
const int maxn=1e6+5;
using namespace std;
int n,m,cnt,head[maxn],s,t,cur[maxn],d[maxn];
bool vis[maxn];
struct node {
int next,to,cap,flow;
} e[maxn<<4];
void Add(int from,int to,int cap) {
e[cnt].cap=cap;
e[cnt].flow=0;
e[cnt].to=to;
e[cnt].next=head[from];
head[from]=cnt++;
}
int getHash(int x,int y) {
return (x-1)*m+y;
}
bool BFS(int s,int t) {
//分层
memset(d,0,sizeof(d));
for(int i=1; i<=getHash(n,m); i++)//复制每个点的head,一定一定要注意节点的个数
cur[i]=head[i];
queue<int>q;
q.push(s);
d[s]=1;
while(!q.empty()) {
int u=q.front();
q.pop();
for(int i=head[u]; ~i; i=e[i].next) {
int v=e[i].to;
if(!d[v]&&e[i].cap>e[i].flow) {
//如果可以增流
d[v]=d[u]+1;
q.push(v);
if(v==t)return 1;
}
}
}
return 0;
}
int DFS(int u,int flow,int t) {
if(u==t)return flow;
int res=flow;//res存储当前节点的可增流值
for(int i=cur[u]; ~i&&res; i=e[i].next) {
//遍历满足条件的邻边并增流
cur[u]=i;//当前弧优化
int v=e[i].to;
if(d[v]==d[u]+1&&e[i].cap>e[i].flow) {
int k=DFS(v,min(res,e[i].cap-e[i].flow),t);//获得最小的回溯流
if(!k) {
d[v]=0;
continue;
}
e[i].flow+=k;//获得最小的回溯流后增流
e[i^1].flow-=k;
res-=k;//可增流值减少,因为已经有邻边增流
}
}
return flow-res;//返回实际的总增流值
}
int Dinic(int s,int t) {
int ans=0;//存储最大流
while(BFS(s,t))ans+=DFS(s,inf,t);
return ans;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
memset(head,-1,sizeof(head));
for(int i=1; i<=n; i++)
for(int j=1; j<=m-1; j++) {
int w;
cin >>w;
Add(getHash(i,j),getHash(i,j+1),w);//加双边,每条边两边都能走
Add(getHash(i,j+1),getHash(i,j),0);
Add(getHash(i,j+1),getHash(i,j),w);
Add(getHash(i,j),getHash(i,j+1),0);
}
for(int i=1; i<n; i++)
for(int j=1; j<=m; j++) {
int w;
cin >>w;
Add(getHash(i,j),getHash(i+1,j),w);
Add(getHash(i+1,j),getHash(i,j),0);
Add(getHash(i+1,j),getHash(i,j),w);
Add(getHash(i,j),getHash(i+1,j),0);
}
for(int i=1; i<n; i++)
for(int j=1; j<m; j++) {
int w;
cin >>w;
Add(getHash(i,j),getHash(i+1,j+1),w);
Add(getHash(i+1,j+1),getHash(i,j),0);
Add(getHash(i+1,j+1),getHash(i,j),w);
Add(getHash(i,j),getHash(i+1,j+1),0);
}
s=1,t=getHash(n,m);
cout <<Dinic(s,t)<<endl;//最小割等价求最大流
return 0;
}
代码(对偶图+最短路)
#include <bits/stdc++.h>
//#define int long long
using namespace std;
typedef pair<int,int>pr;
const int maxn=1e6+5;
const int inf=0x3f3f3f3f;
int n,m,cnt,head[maxn<<4],s,t,d[maxn<<4];
bool vis[maxn<<4];
struct node {
int next,to,w;
} e[maxn<<4];
void Add(int from,int to,int w) {
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].w=w;
head[from]=cnt;
}
void Dijkstra() {
priority_queue<pr,vector<pr>,greater<pr>>q;
d[s]=0;
q.push({
d[s],s});
while(!q.empty()) {
auto u=q.top();
q.pop();
int p=u.second;
if(vis[p])continue;
vis[p]=1;
for(int i=head[p]; ~i; i=e[i].next) {
int v=e[i].to;
if(d[v]>d[p]+e[i].w)
q.push({
d[v]=d[p]+e[i].w,v});
}
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n>>m;
t=n*m*2+1,s=0;
for(int i=s; i<=t; i++)d[i]=inf;
memset(head,-1,sizeof(head));
for(int i=1; i<m; i++) {
int w;
cin >>w;
Add(i,t,w);//第一行的所有横边与t相连
Add(t,i,w);
}
for(int i=2; i<n; i++)
for(int j=1; j<m; j++) {
int w;
cin >>w;
int u=(i-1)*(m-1)*2+j,v=(i-1)*(m-1)*2+j-m+1;
//多加了一个(i-1)*(m-1),相当于偏移量
Add(u,v,w);
Add(v,u,w);
}
for(int i=1; i<m; i++) {
int w;
cin >>w;
int v=(n-2)*(m-1)*2+m+i-1;
//相当于i=n-1
Add(s,v,w),Add(v,s,w);
}
for(int i=1; i<n; i++) {
int w;
cin >>w;
Add((m-1)*2*(i-1)+m,s,w);
Add(s,(m-1)*2*(i-1)+m,w);
for(int j=2; j<m; j++) {
cin >>w;
int u=(m-1)*2*(i-1)+m+j-1,v=(m-1)*2*(i-1)+j-1;
Add(u,v,w);
Add(v,u,w);
}
cin >>w;
Add((m-1)*2*(i-1)+m-1,t,w);
Add(t,(m-1)*2*(i-1)+m-1,w);
}
for(int i=1; i<n; i++)
for(int j=1; j<m; j++) {
int w;
cin >>w;
int u=(m-1)*(i-1)*2+j,v=(m-1)*(i-1)*2+j+m-1;
Add(u,v,w),Add(v,u,w);
}
Dijkstra();
cout <<d[t]<<endl;
return 0;
}
LuoguP2046
题目大意:略
思路:
代码
LuoguP7916
题目大意:略
思路:
代码
LuoguP1514
题目大意:
思路:
代码
2020牛客多校第二场 I
题目大意:
思路:
代码
总结
参考文献
- 平面图最小割与对偶图最短路
- 平面图上最小割=对偶图最短路
- 图论 —— 网络流 —— 最小割 —— 平面图与对偶图
- 《两极相通——浅析最大最小定理在信息学竞赛中的应用》
- P4001 [ICPC-Beijing 2006] 狼抓兔子 题解
边栏推荐
猜你喜欢
随机推荐
FreeRTOS创建任务--动态创建、静态创建
如何搭建威纶通触摸屏与S7-200smart之间无线PPI通信?
js源码跳转的几种方式,在当前页面跳转,在空白页跳转
sql concat()函数
Introduction to Graph Neural Networks (GNN) "Recommended Collection"
ETL(二):表达式组件的使用
Seneor Exposure Basics
package.json与package-lock.json
String concatenation in SQL
手撸架构,Redis面试41问
package.json and package-lock.json
np.nan, np.isnan, None, pd.isnull, pd.isna finishing and summary
#Summer Challenge#[FFH] OpenHarmony Device Development Foundation (3) Compilation Dependencies
如何关闭开启硬件加速[通俗易懂]
np.nan, np.isnan, None, pd.isnull, pd.isna 整理与小结
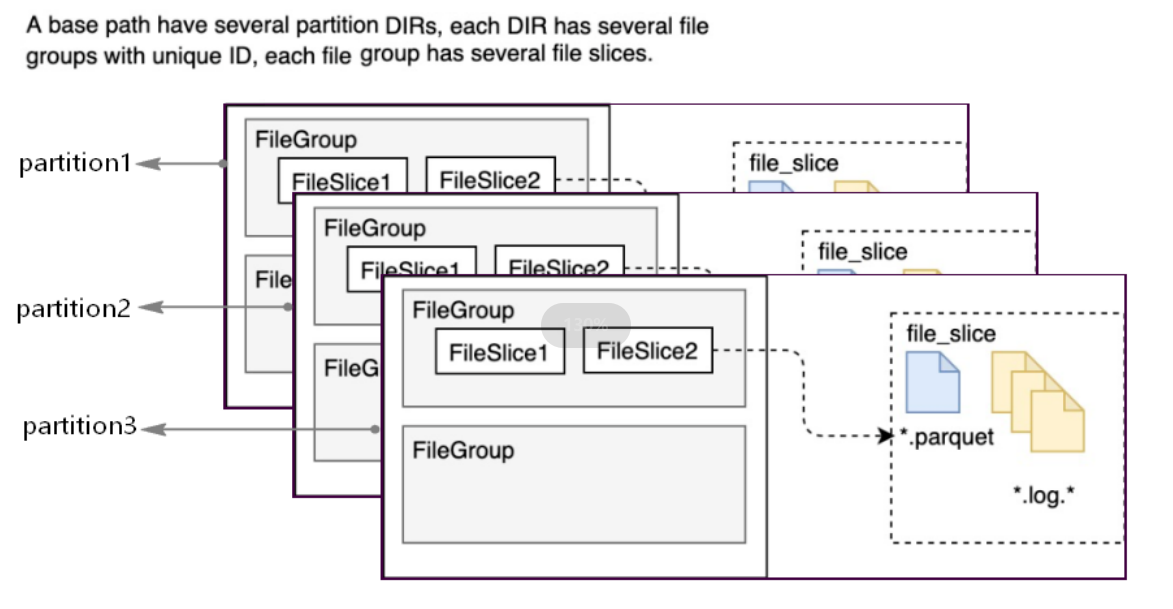
数据湖(三):Hudi概念术语
无线振弦采集仪远程修改参数方式
FreeRTOS--栈实验
技术分享| 融合调度系统中的电子围栏功能说明
WPF——自定义日历