【论文笔记】基于动作空间划分的MAXQ自动分层方法

摘要

• 针对问题：分层强化学习需要人工给出层次结构这一问题；基于状态空间的自动分层方法在环境状态中没有明显子目标时分层效果并不理想
• 提出方法：基于动作空间的自动构造层次结构方法；对MAXQ的子任务终止条件进行修改；
• 细节：动作集合划分子集 $\to$ 不同状态下识别瓶颈动作 $\to$ 确定动作子集之间的上下层关系 $\to$ 构造层次结构
• 结果：与Q/SARSA相比，可以自动构建层次，具有鲁棒性；

关键词

• 强化学习;
• 分层强化学习;
• 自动分层方法;
• 马尔可夫决策过程;
• 子任务;

0 引言

减小“维数灾难”的影响 $\to$ 将分层、抽象等机制引入强化学习 $\to$ 本质是：既对状态空间进行降维、又实现任务分层 $\to$ 较小的低维空间中逐步解决子任务

主流：MAXQ、Option和HAM
HAM $\to$Hierarchies of Abstract Machine 分层抽象机
共同点 $\to$ 需要先验知识

学者	提出	特点
Hengst	HEXQ 方法	状态变量的改变次数进行排序
McGovern 和 Stolle	划分子任务方法	通过寻找瓶颈状态来划分子任务
Mehta	HI-MAT（Hierarchy Induction via Models And Trajectories）	动态贝叶斯网络 + 一条已知的成功轨迹 $\to$ 一条带因果注释轨迹，在此基础上划分任务
石川	构造Option的方法	利用单向值识别出瓶颈状态
沈晶	OMQ 算法	自动构造 Option，子任务插入到到MAXQ 任务图中

本文工作：

1. 提出一种自动分层算法；
2. 提出了一种新的判断子任务是否结束的方法；

1 马尔可夫决策过程与分层强化学习

1.1 马尔可夫决策过程

分层强化学习会对原始问题进行抽象
$\to$ 可执行的动作会被替换为需要多个时间步完成的宏动作
$\to$ 引入"半马尔可夫决策过程"SMDP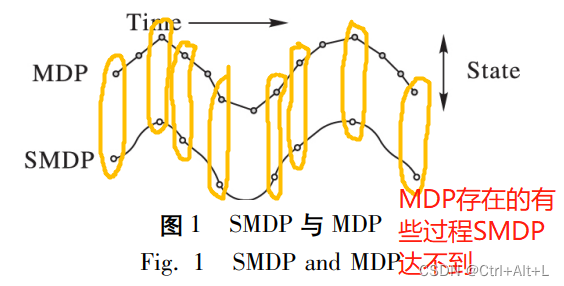

SMDP可以分为离散SMDP和连续SMDP
离散SMDP的时间间隔是单步间隔的整数倍
值函数与Q函数在单步间隔的基础上增加额外的单步间隔奖励就行

1.2 分层强化学习

1. 分层强化学习的抽象方法分类：

分类	特点
状态抽象	忽略与当前问题无关的状态分量，减小空间
时态抽象	单次执行的基本动作拓展为需要多个时间步执行的抽象动作 $\to$ 相当于一套一套地决策，能减少决策次数
状态空间分解	将原始的状态空间分解为多个子空间

2. 典型的强化学习方法分类：

分类	特点
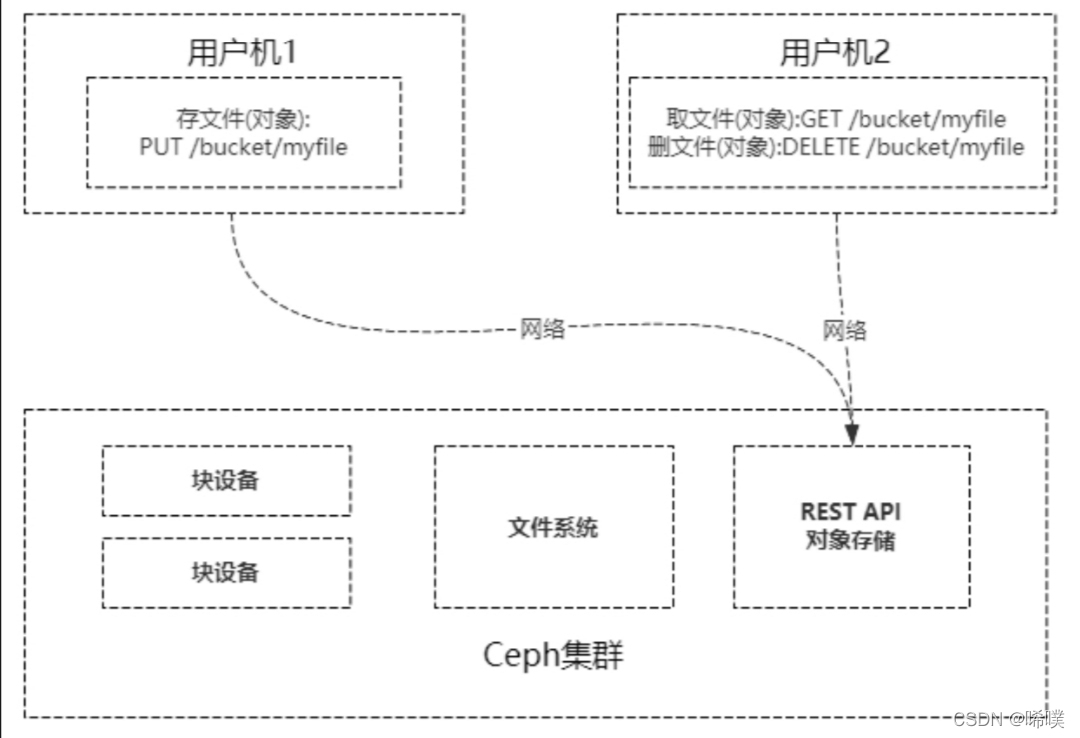
Option	（1）将学习任务抽象为若干Option，每个 Option 都是一个为完成子任务而定义在状态空间上的动作序列。(Option $\to$ 一套动作序列)（2）这些 Option 作为一种抽象动作加入到原来的动作集中。（动作集里面包含了一些基本动作和这些基本动作组合成的子集）（3）Option内部自己进行强化学习。（4）智能体只需要对Option（本身含义就是"选项"）进行选择。
MAXQ	（1）将原始任务分解为子任务和子策略；（2）子任务可以是不可再划分的原子型子任务和组合型子任务；（3）子任务以最初的任务为根节点，组成了任务图，在任务图中先解决下层子任务再解决上层子任务；（4）需要根据学习的策略改变任务图。
HAM	（1）将MDP过程分解为多个子任务 $\to$ 多个随机有限状态机（2）当前随机有限状态机所处的内部状态可以执行动作、改变内部状态、调用别的随机有限状态机或者返回调用自己的随机有限状态机。

1.3 MAXQ 值函数分解

MAXQ的核心 $\to$ MAXQ的值函数分解

$a$既可能是原子型动作，也可能是组合型动作

引入完成函数后可以对Q函数分解成当前的即时奖励和一系列的完成函数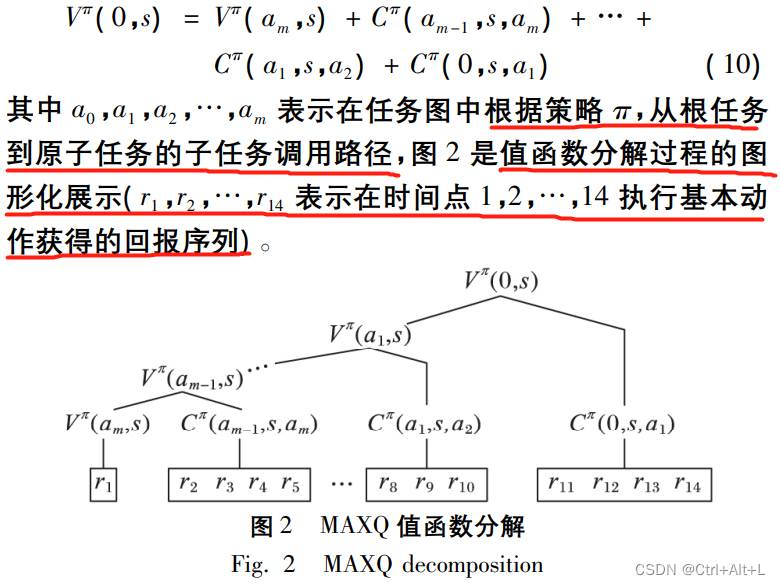

2 基于动作的层次结构划分方法

2.1 动作空间划分的基本思想

识别子目标的常用标准：
访问次数、访问次数落差变化率、单向值
优点 $\to$ 在简单有限的环境中效果较好
缺点 $\to$ 连续环境、高维环境表现不好

本文提出一种不需考虑外部环境，只通过划分动作空间构造分层结构的方法。
思路：状态 $\to$ 抽象成一维的向量 $\to$ 记录动作的一维向量分量的影响；
原则：执行次数多的子任务 $\to$ 下层；执行次数高 $\to$ 上层；
引入瓶颈动作：不执行该动作无法进入下一个子任务 。
$\to$ 特殊地：某个状态下只有一个动作，这个就是瓶颈动作。
$\to$ 意义：判断子任务是否完成/结束的标志；两个瓶颈动作之间的普通动作走行的状态应该划分成一个子任务。
$\to$ 在构造分层结构时，记录下瓶颈动作之间的动作执行轨迹(即动作$a$) ，以及动作$a$的执行次数$f_a$。

子任务$M_i$的访问频率计算式：

可以认为访问次数比 $M_b$ 高的 $M_a$ 在任务图中位于 $M_b$ 的上层，反之则位于 $M_b$的下层。

2.2 自动分层算法描述

步骤	具体信息
输入	动作集 A
输出	根任务，层次结构
1	执行随即策略；统计基本动作执行的次数；划分动作子集
2	根据动作子集的大小，划分复合型任务或者原子型任务
3	执行随即策略；
4	记录执行轨迹和上下层子任务
5	达到终止状态？跳转到11步，记录基本动作序列集合
6	序列集合大于1，在执行轨迹后添加随即动作，返回5步
7	序列集合等于1，当前动作是瓶颈动作，对应任务是根任务；比较前序动作和瓶颈动作的访问频率；
8
9
10	执行瓶颈动作，跳转到4步
11	子任务构造完成

2.3 子任务的终止条件

本文提出一种通过比较当前状态的可用动作和当前子任务包含的基本动作
判断是否终止当前子任务的方法

3 实验与分析

3.1 实验设置

基本动作：东、西、南、北、加燃料、接乘客和放下乘客
奖励函数设置：

1. 因为受到墙壁或燃料限制而无法移动，-10
2. 执行加燃料动作，-1
3. 成功接到乘客或放下乘客，20
4. 没有在正确位置执行，-10

为了增加环境的复杂性 $\to$ 有 30% 的概率重新选择出租车的起点、乘客所在的站台和目的地

3.2 实验结果与分析

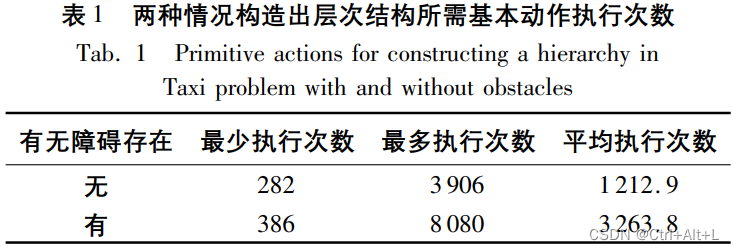
实验结论：

1. 经过自动分层的 MAXQ 方法在整个实验过程中变化趋势较为平稳
2. 前期：比较少的动作执行数完成任务
3. 理由：在完成子任务的过程中可以忽略那些和完成该子任务无关的动作
4. 平均回报的变化趋势：MAXQ较好
5. MAXQ用的时间最少，比Q和SARSA

4 结语