[dynamic programming] - Knapsack Problem

---

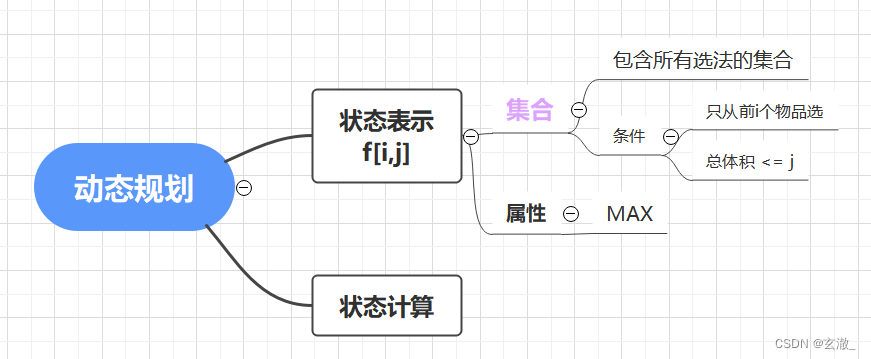
Classification of knapsack problem

---

01 knapsack problem  

sample input

4 5
1 2
2 4
3 4
4 5

sample output ：

8

---

  In the process of selection The first i The state transition equation of an object , We can take it out    The maximum value of plus w[i]

No second choice i If it's an item , The equation of state transition is    

 

---

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

---

From two-dimensional optimization to one-dimensional optimization  

adopt   DP State transfer equation of , We found that , At each stage i The state of is only related to that of the previous stage i-1 The state of . under these circumstances , It can be used as “ Scrolling array ” Optimization method , Reduce time overhead . 

because    there    Certain ratio    Calculated earlier , therefore    The result of calculation is i Layer of , And in our above DP Fang Chengzhong , What is used is The first i - 1 layer The data of , So if you traverse the volume from small to large , There will be “ Data pollution ” The situation of . So the enumeration of volume should be from large to small .

One dimensional optimization code implementation

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = m; j >= v[i]; j -- )
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
        
    cout << f[m] << endl;
    return 0;
}

---

Complete knapsack problem

sample input

4 5
1 2
2 4
3 4
4 5

sample output ：

10

---

 

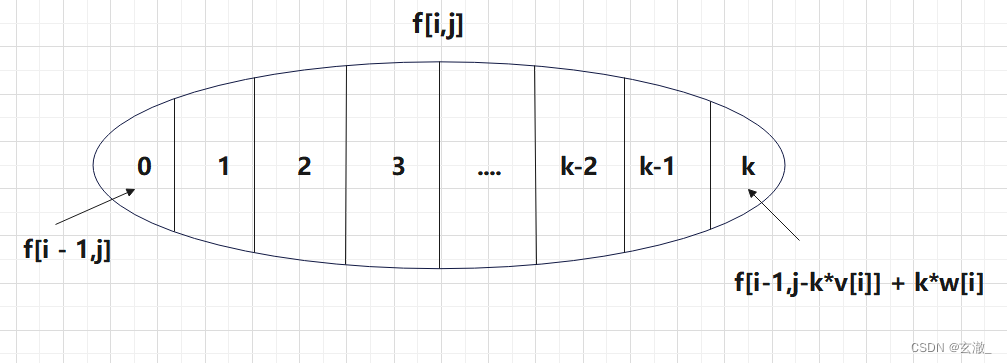
about Simple approach Yes ：   analogy 01 knapsack problem

Code implementation

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int k = 0; k * v[i] <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    cout << f[n][m] << endl;
    
    return 0;
}

---

By comparing the following equations, we can find that ：

obtain ： 

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    
    return 0;
}

---

One dimensional optimization

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = v[i]; j <= m; j ++ )
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    cout << f[m] << endl;
    
    return 0;
}

contrast 01 knapsack and Completely backpack problem , There are the following differences  ：

01 knapsack ：

Completely backpack ：

For a complete backpack , The enumeration of volumes can from v[i] Enumerate to m, Because it every i Layer update I'm using a number i Layer data , non-existent “ Data pollution ” The problem of .

---

  Multiple knapsack problem

sample input

4 5
1 2 3
2 4 1
3 4 3
4 5 2

sample output ：

10

---

 

 

---

Plain writing  

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
    cout << f[n][m] <<  endl;
    
    return 0;
}

---

Binary optimization of multiple knapsacks  

as everyone knows , from    this k individual 2 Select several addition from the integer powers of , It can show    Any integer between . further , We find satisfaction    Maximum integer for p, set up   that ：

1. according to p The maximum of , Yes   , Can be launched  , therefore    Choose a number of additions to show    Any integer between ;
2. from    Select several of them to add , It can show    Any integer between , According to the Ri The definition of , , therefore ,  Choose a few to show   Any integer between .

in summary , We can take the quantity as    Of the i Break an item into p + 2 Items , Their volumes are ：

        

this p + 2 Items can be put together    Between all can be Vi Divisible number , And can not be rounded up to be greater than Ci * Vi Number of numbers . This is equivalent to the volume in the original problem being Vi Can use 0~Ci Time . This method only splits each item into    individual , More efficient .

Code implementation

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 25000, M = 2010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    
    int cnt = 0;
    for(int i = 1; i <= n; i ++ )
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while(k <= s)
        {
            cnt ++ ;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0)
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    
    for(int i = 1; i <= n; i ++ )
        for(int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    
    cout << f[m] << endl;
    
    return 0;
}

---

  Group knapsack problem

sample input

3 5
2
1 2
2 4
1
3 4
1
4 5

sample output ：

8

---

---

AC Code  

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++ )
    {
        cin >> s[i];
        for(int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1; i <= n; i ++ )
        for(int j = m; j >= 0; j -- )
            for(int k = 0; k < s[i]; k ++ )
                if(v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    
    cout << f[m] << endl;
    
    return 0;
}