Lecture 1 number field

1. introduce

Number is one of the most basic concepts in Mathematics , Review the development of numbers we have learned :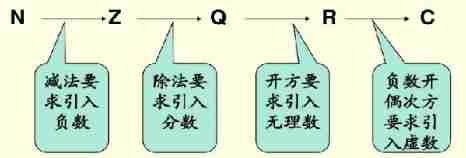

(1) Algebraic properties : On the addition of numbers , reduce , ride , The property of division is called the algebraic property of numbers .
(2) Number set : The set of numbers is abbreviated as the set of numbers .
Common number sets : Second interview C; The set of real Numbers R; Rational number Q wait . They have a common property that they are closed to addition, subtraction, multiplication and division .

2. Definition of number field

set up F It's a collection of complex numbers , These include 0 and 1, If F The sum of any two numbers in , Bad , product , merchant ( The divisor is not 0) Throw yes F The number in , said F For one Number field .
From the definition of number field, we can see that a number field should meet :

• Is a subset of the complex number ;
• contain 0 and 1;
• Close the operation of addition, subtraction, multiplication and division .

Common number fields : Complex field C, Real number field R, Rational number field Q. ( Set of natural numbers N And the set of integers Z It's not a number field .)
Be careful :
(1) If number set F The result of some operation on any two numbers in is still F in , We call it a set of numbers F For this operation closed Of .
(2) The equivalent definition of number field : If one contains 0, 1 The set of numbers in F For addition , Subtraction , Multiplication and division ( The divisor cannot be zero 0) It's all closed , We call it a set of numbers F Is a number field .

Well, in addition to the rational field Q, Real number field R And complex fields C Outside , Are there any other number fields ? Of course. !

example 1. prove : Number set $Q(\sqrt{2})=\{a+b\sqrt{2}|a,b\in Q\}$ It's a number field .
prove :
(1) $\{a+b\sqrt{2}|a,b\in Q\}\subseteq C$
(2) because $0=0+0\sqrt{2},1=1+0\sqrt{2}$, therefore $0,1\in Q(\sqrt{2})$
(3) set up $a,b,c,d\in Q$, Then there are
$x\pm y=(a\pm c)+(b\pm d)\sqrt{2}\in Q(\sqrt{2}),$
$x.y=(ac+2bd)+(ad+bc)\sqrt{2}\in Q(\sqrt{2})$
set up $a+b\sqrt{2}\ne 0$, Then there are $a-b\sqrt{2}\ne 0$

( otherwise , if $a-b\sqrt{2}=0$, be $a=b\sqrt{2}$,
\quad So there is $\frac{a}{b}=\sqrt{2}\in Q$
\quad or $a=0,b=0\Rightarrow a+b\sqrt{2}=0$ All contradictions )

$\frac{c+d\sqrt{2}}{a+b\sqrt{2}}=\frac{(c+d\sqrt{2})(a-b\sqrt{2})}{(a+b\sqrt{2})(a-b\sqrt{2})}=\frac{ac-2bd}{a^2-2b^2}+\frac{ad-bc}{a^2-2b^2}\sqrt{2}\in Q(\sqrt{2})$

therefore , $Q(\sqrt{2})$ It's a number field .
Can prove similar $\{a+b\sqrt{p}|a,b\in Q\},pbyplainCount$, Are all numeric fields , So there are infinite number fields .

example 2: set up F Is a set of numbers containing at least two numbers , prove : if F The difference and quotient of any two numbers in ( The divisor is not 0) Still belong to F, be F Is a number field .

prove : Choose from the question set $a,b\in F$, Yes
$0=a-a\in F,1=\frac{b}{b}\in F(b\ne 0)$,
$a-b\in F,\frac{a}{b}\in F(b\ne 0)$,
$a+b=a-(0-b)\in F$,
$b\ne 0when,ab=\frac{a}{\frac{1}{b}}\in F,b=0when,ab=0\in F$,
therefore , F It's a number field .

3. Properties of number fields

nature 1: Any number field F They all include the rational number field Q. namely , The rational number field is the minimum number field .
prove :
set up F For any number field . By definition :
$0\in F,1\in F.$
So there is
$\forall m\in Z^{+},m=1+1+...+1\in F$
And then there are
$\forall m,n\in Z^{+},\frac{m}{n}\in F$,
$-\frac{m}{n}=0-\frac{m}{n}\in F$.
Any rational number can be expressed as the quotient of two integers , therefore
$Q\subseteq F$