当前位置:网站首页>线性表的查找
线性表的查找
2022-08-05 01:59:00 【马可爱家的马可爱】
1、顺序查找
(1)顺序查找介绍
顺序查找的查找过程为:从表的一端开始,依次将记录的关键字和给定的值进行比较,若某个记录的关键字和给定的值是一样的,则查找成功;反之,若扫描整个表之后,任然没有找到关键字和给定的值相等的记录,则查找失败!
适用用线性表和链表!
(2)、代码实现
(1)、顺序查找
//顺序查找
int Search_Seq(SSTable S,int key){
for (int i = S.length - 1; i >= 1 ; i-- ) //i = S.length - 1,S.data[S.length - 1] = -1结束标志符
{
if (S.data[i] == key)
return i; //从前往后查找成功!
}
return 0; //查找失败
}
但是上面的算法中每一步都要检查整个表是否查找完毕,即每次循环都要判断循环变量 i >= 1 的检测。下面设置哨监视的查找算法就是对这种情况的改进!
(2)、设置哨监视的顺序查找
哨监视的顺序查找是将查找值 key 放在S.data[0]中,然后执行操作!
//哨监视的顺序查找
int Search_Seq1(SSTable S,int key){
//从后往前找直到 i = 0,此时是查找失败;否则会返回 1 ~ S.length - 1 之间的位置数
int i;
S.data[0] = key;
for ( i = S.length - 1; S.data[i] != key ; i-- );
return i;
}
这个算法当S.length >= 1000的时候,进行查找的实际几乎会减少一半
(3)、所有代码如下
#include<string.h>
#include<stdio.h>
#define MaxSize 20
#include<iostream>
#include<stdlib.h>
#define endl '\n'
using namespace std;
typedef struct{
int *data;
int length;
}SSTable;
void InputElement(SSTable &S){
S.data = (int *) malloc (sizeof(int)*MaxSize);
S.length = 1;
cout<<"\n请输入要排序的数!结束请输入 -1 :";
for (int i = 1 ; i < MaxSize && S.data[i-1] != -1; i++){
//将S.data[0]闲置不用
cin>> S.data[i];
S.length++;
}
int i = 1;
cout<<"\n输入如下:";
while(S.data[i] != -1){
cout<<S.data[i]<<" ";
i ++;
}
}
//顺序查找
int Search_Seq(SSTable S,int key){
for (int i = S.length - 1; i >= 1 ; i-- ) //i = S.length - 1,S.data[S.length - 1] = -1结束标志符
{
if (S.data[i] == key)
return i; //从前往后查找成功!
}
return 0; //查找失败
}
//哨监视的顺序查找
int Search_Seq1(SSTable S,int key){
//从后往前找直到 i = 0,此时是查找失败;否则会返回 1 ~ S.length - 1 之间的位置数
int i;
S.data[0] = key;
for ( i = S.length - 1; S.data[i] != key ; i-- );
return i;
}
main(){
SSTable S;
InputElement(S);
cout<<"\n\n请输入查找关键字:";
int key;
cin>>key;
if (Search_Seq(S,key))
cout<<"\n查找成功!在顺序表中是第 "<<Search_Seq(S,key)<<" 个元素!\n";
else
cout<<"\n查找失败!\n";
cout<<"\n-----------------------------------------前后对比如下-----------------------------------------------------\n";
if (Search_Seq1(S,key))
cout<<"\n查找成功!在顺序表中是第 "<<Search_Seq1(S,key)<<" 个元素!\n";
else
cout<<"\n查找失败!\n";
}
(4)、结果测试
(3)、算法分析
顺序查找的优点是:算法简单,对表结构没有任何的要求,既适用于顺序结构,同时又适用于链式结构,无论记录按关键字是否有序均可应用!但是其平均查找长度ASL比较大,ASL = 1/n * (1 + 2 + 3 + …+ n) = (n + 1)/2,所以其查找效率很低。当查找个数n很大的时候,不适合采用顺序表!
2、折半查找(二分查找)
(1)、二分查找介绍
折半查找是一种效率较高的查找方法,但是折半查找要求线性表必须采用顺序存储结构,因为顺序表拥有比随机存取访问的特性,而链表没有,故不能使用链表实现二分查找!并且表中的元素必须有序,要么升序要么降序,如果不是则无法使用实现对比折半查找(下面的代码实现中假定是升序)
从表的中间记录开始,如果查找的值和中间记录的值相等,则查找成功;如果查找值和大于或者小于中间记录的关键字,则在表中大于或小于中间记录的那一半中查找,这样重复操作,直到查找成功!或者在某一步中查找区间为空,则代表查找失败!
(2)、代码实现
#include<string.h>
#include<stdio.h>
#define MaxSize 20
#include<iostream>
#include<stdlib.h>
#define endl '\n'
using namespace std;
typedef struct{
int *data;
int length;
}SSTable;
//输入数
void InputElement(SSTable &S){
S.data = (int *) malloc (sizeof(int)*MaxSize);
S.length = 1;
cout<<"\n请输入要排序的数!结束请输入 -1 :";
for (int i = 0 ; i < MaxSize && S.data[i-1] != -1; i++){
cin>> S.data[i];
S.length++;
}
int i = 0;
cout<<"\n输入如下:";
while(S.data[i] != -1){
cout<<S.data[i]<<" ";
i ++;
}
}
int Search_Bin(SSTable S,int key){
int low = 0, high = S.length -1,mid;
while(low <= high){
//查找成功的情况
mid = (low + high)/2;
if (S.data[mid] == key)
return mid;
else if(S.data[mid] > key)
high = mid - 1;
else
low = mid + 1;
}
return 0; //查找失败,即low > high
}
main(){
SSTable S;
InputElement(S);
cout<<"\n\n请输入查找关键字:";
int key;
cin>>key;
if (Search_Bin(S,key))
cout<<"\n查找成功!在顺序表中是第 "<<Search_Bin(S,key)+1<<" 个元素!\n";
else
cout<<"\n查找失败!\n";
}
当 low = high的时候,查找区间还有最后一个元素需要执行判断操作!
(3)、算法分析
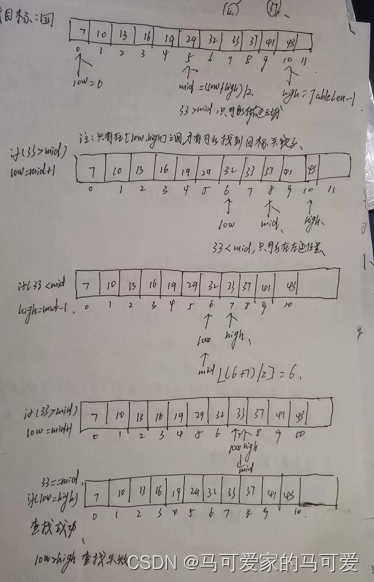
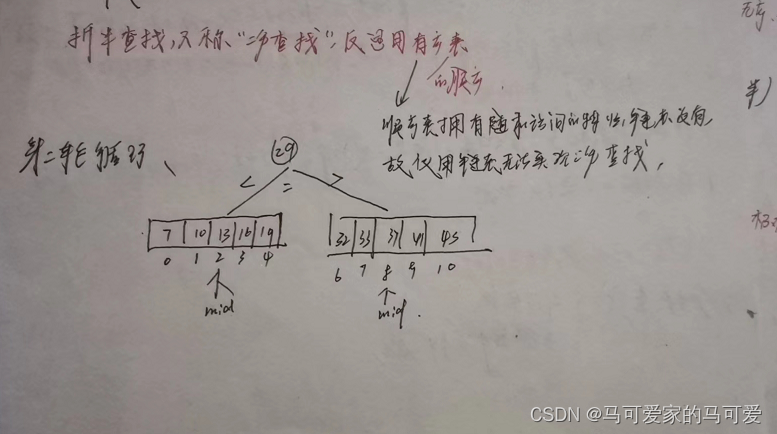
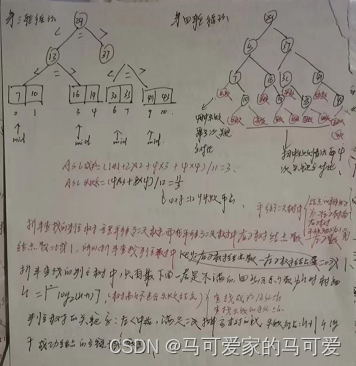
所以折半查找可以使用二叉树来描述!由此可见,折半查找在查找成功的时候进行比较的关键字个数一定不超过树的深度!而判定树的形态只与表记录的个数 n 有关,而与关键字的取值无关!在第五章我们知道,具有n个节点的二叉树的高为 h = 【log 2 n】+ 1(向下取整);或h = 【log 2 (n+1)】向上取整。因此折半查找在查找成功的时候和给定值进行比较的关键字个数至多不超过 树高h!
判定树的关键字:左 < 中 < 右,满足 二叉排序树 的定义,失败节点为 n + 1个,是成功节点空链域的个数,所以查找失败的时候和给定值进行比较的关键字个数最多也超过 树高h!
所以折半查找的时间复杂度是O(log 2 n)!
折半查找的优点是:查找次数少,查找效率高,但是必须是有序的顺序表,而不是链表!并且,查找前必须排序!同时为了保持顺序表的有序性,对表进行插入或者删除的时候,平均要比较移动表中一半的元素。因此,折半查找不适合使用于数据元素经常变动的线性表!
(4)、平均查找长度
ASL = (n+1)/n * log2 (n + 1)- 1 当n较大的时候可以直接取为ASL = log2 (n + 1)- 1
3、分块查找(索引顺序查找)
(1)、分块查找介绍
是一种性能介于顺序查找和折半查找之间的一种查找方法!
分块查找的基本思想:
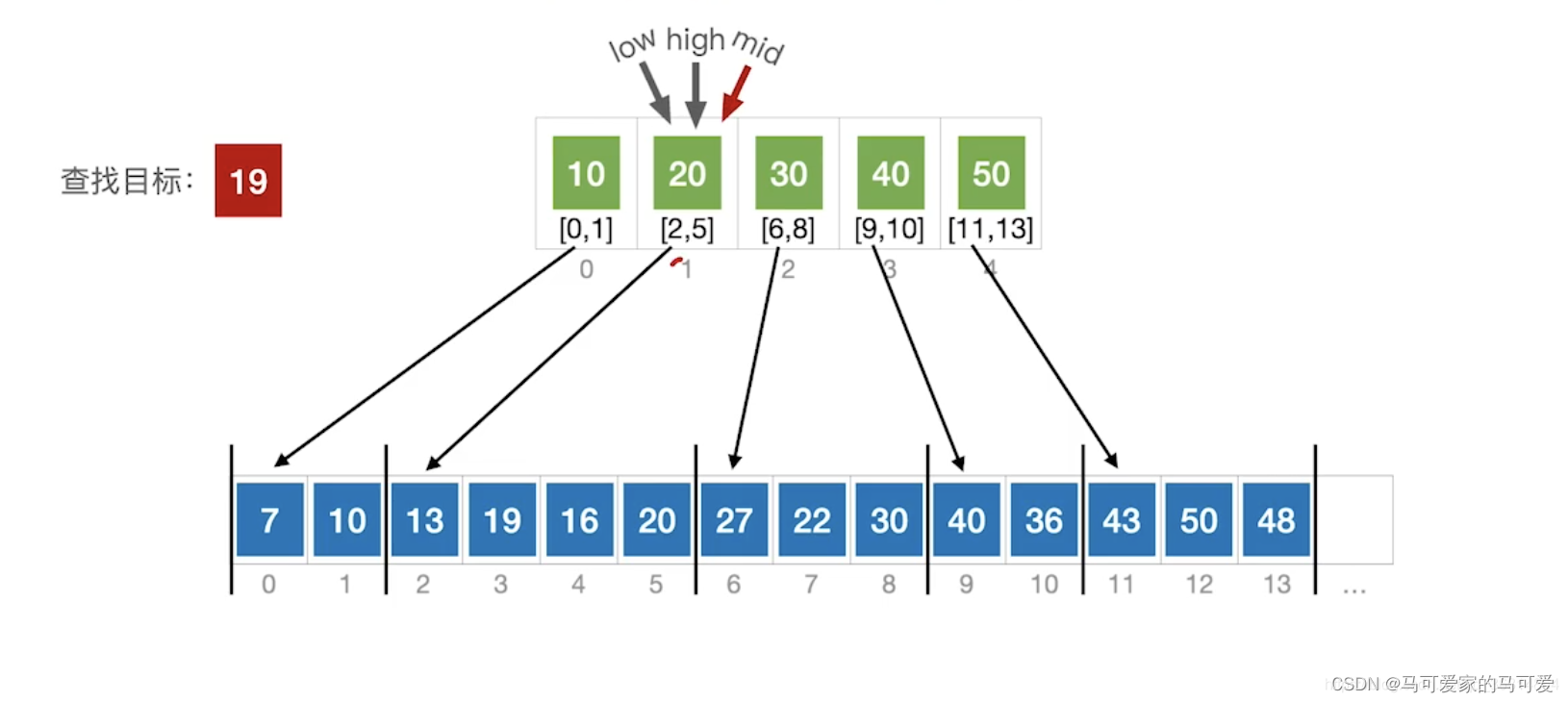
将查找表分为若干子块。块内的元素可以无序,但块之间是有序的,即第一个块中的最大关键字小于第二个块中的所有记录的关键字,第二个块中的最大关键字小于第三个块中的所有记录的关键字,以此类推。再建立一个索引表,索引表中的每个元素含有各块的最大关键字和各块中的第一个元素的地址,索引表按关键字有序排列(王道中是每个元素含有各块的最大关键字和各块中的第一个元素的地址和最后一个元素的地址)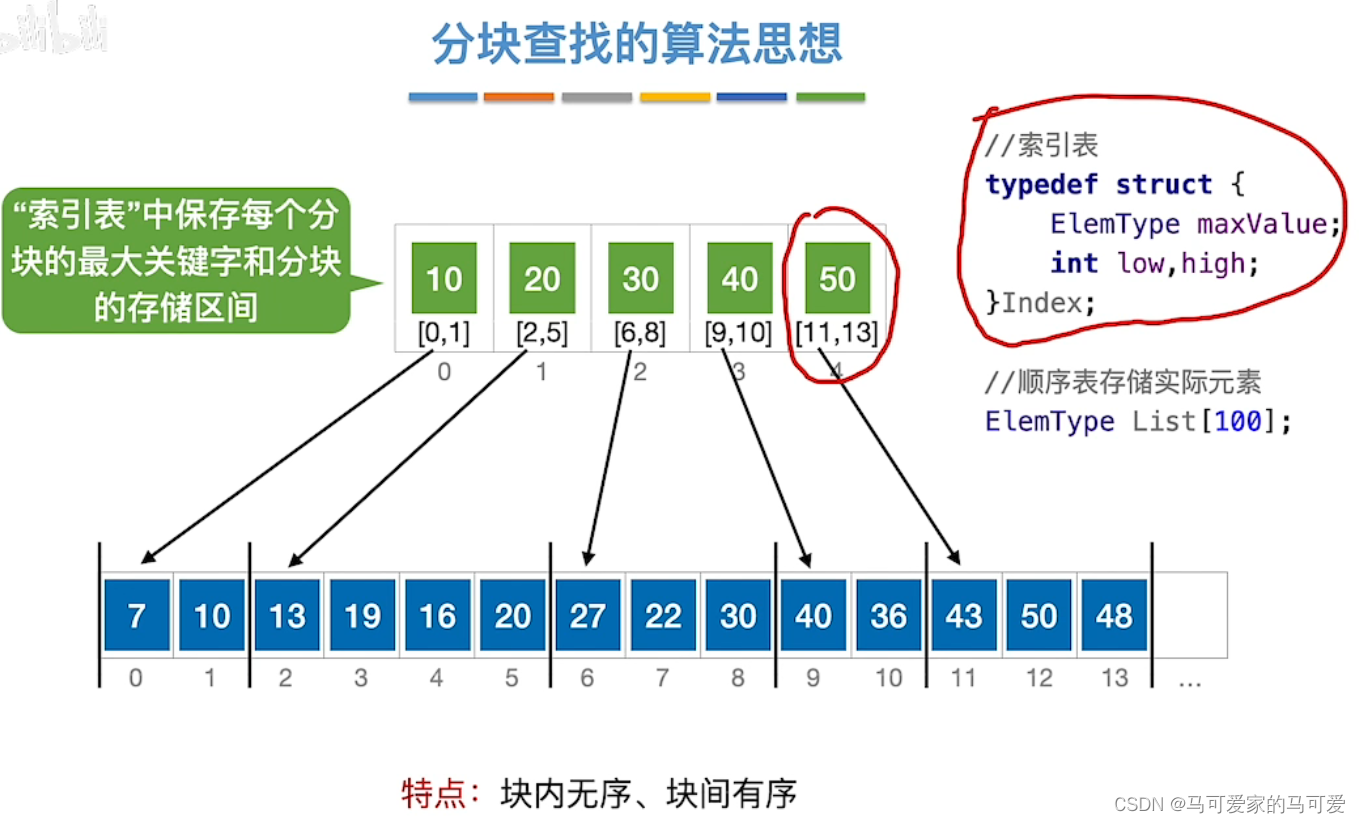
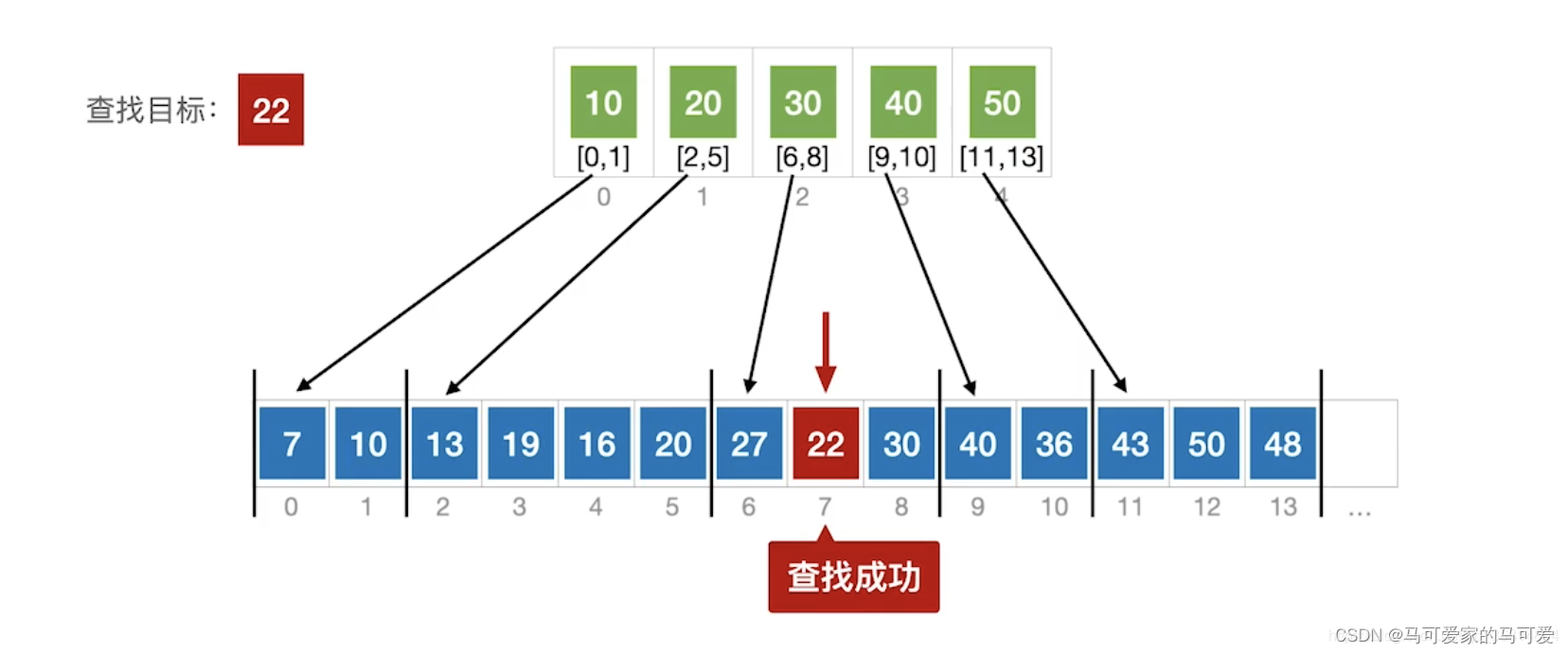
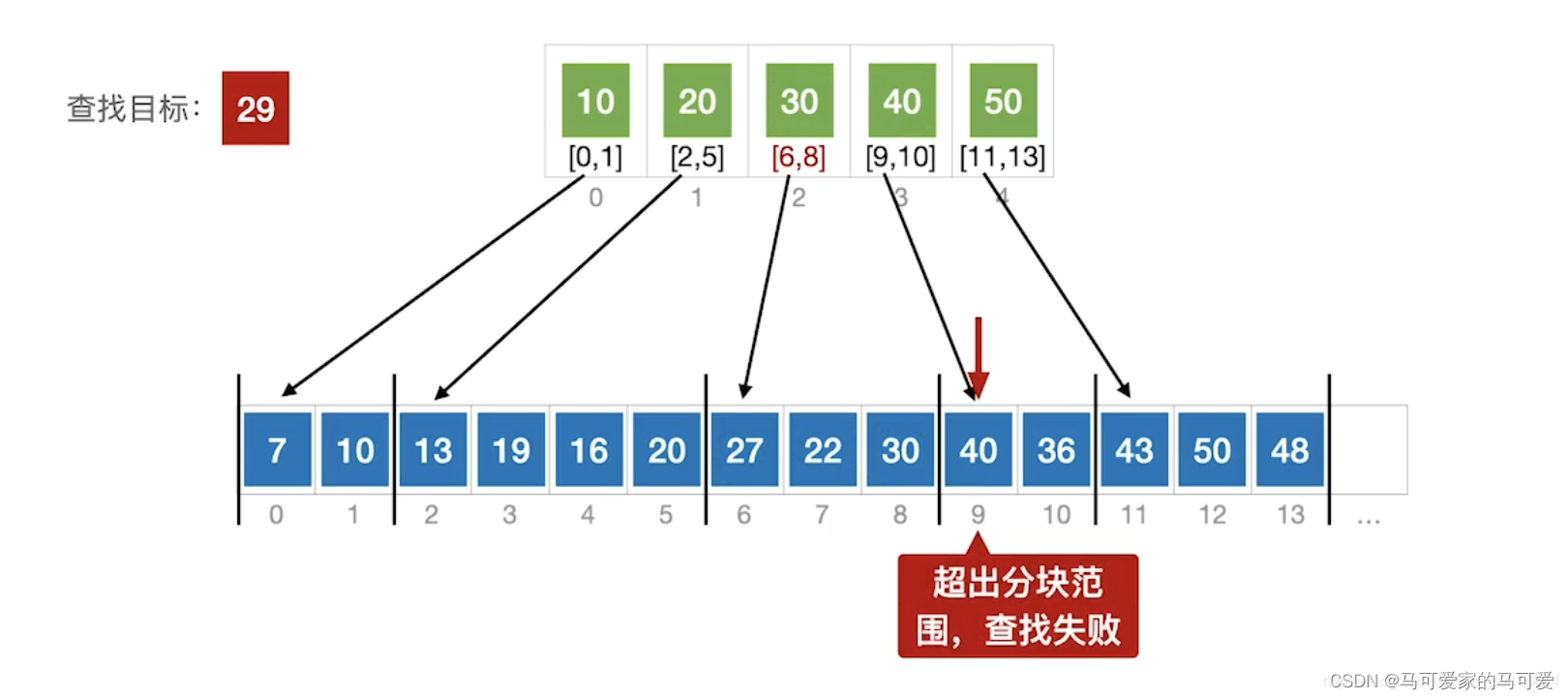
(2)、分块查找的过程
● 第一步是在索引表中确定待查记录所在的块,可以顺序查找或折半查找索引表。
● 第二步是在块内顺序查找。
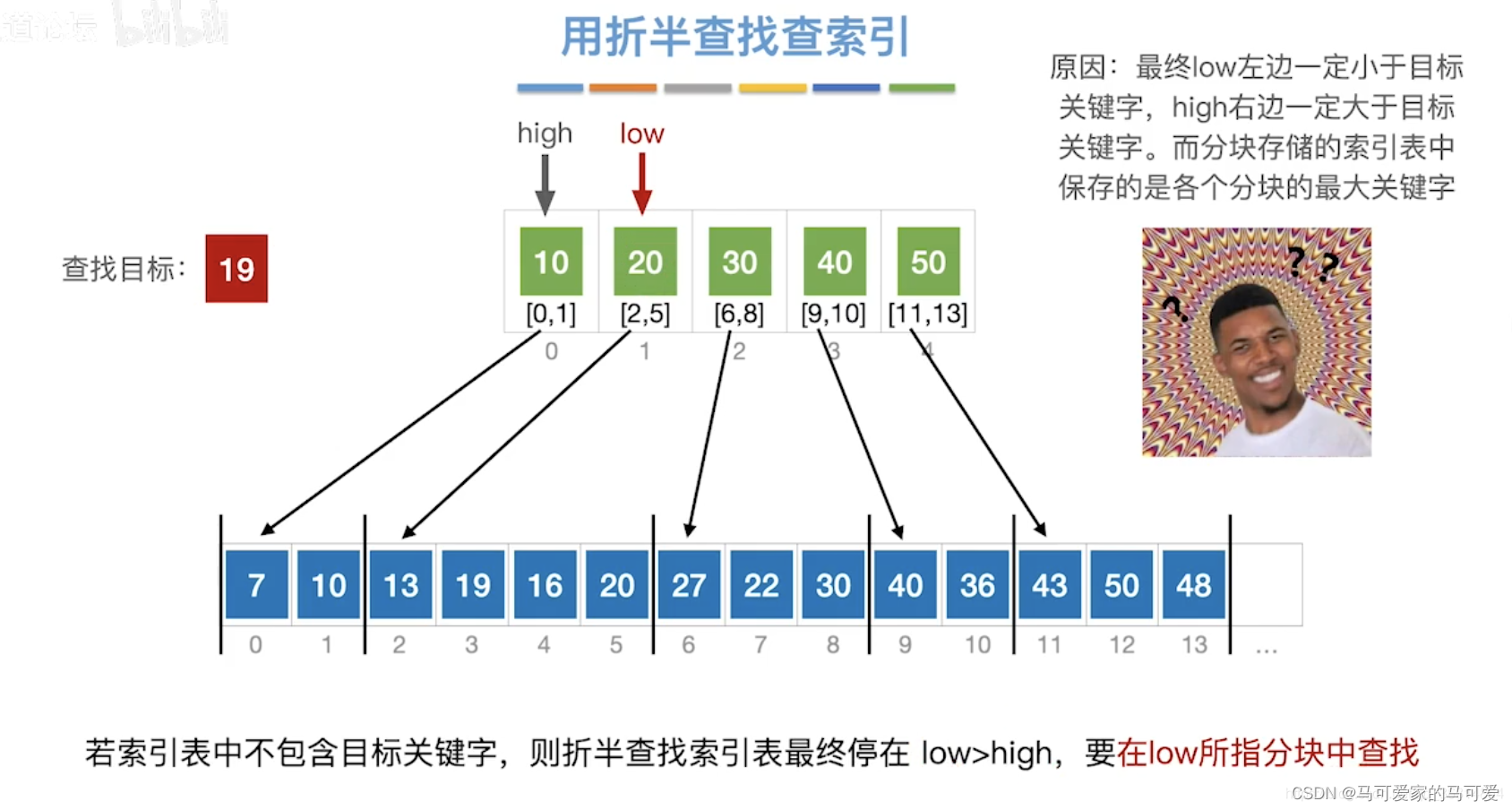
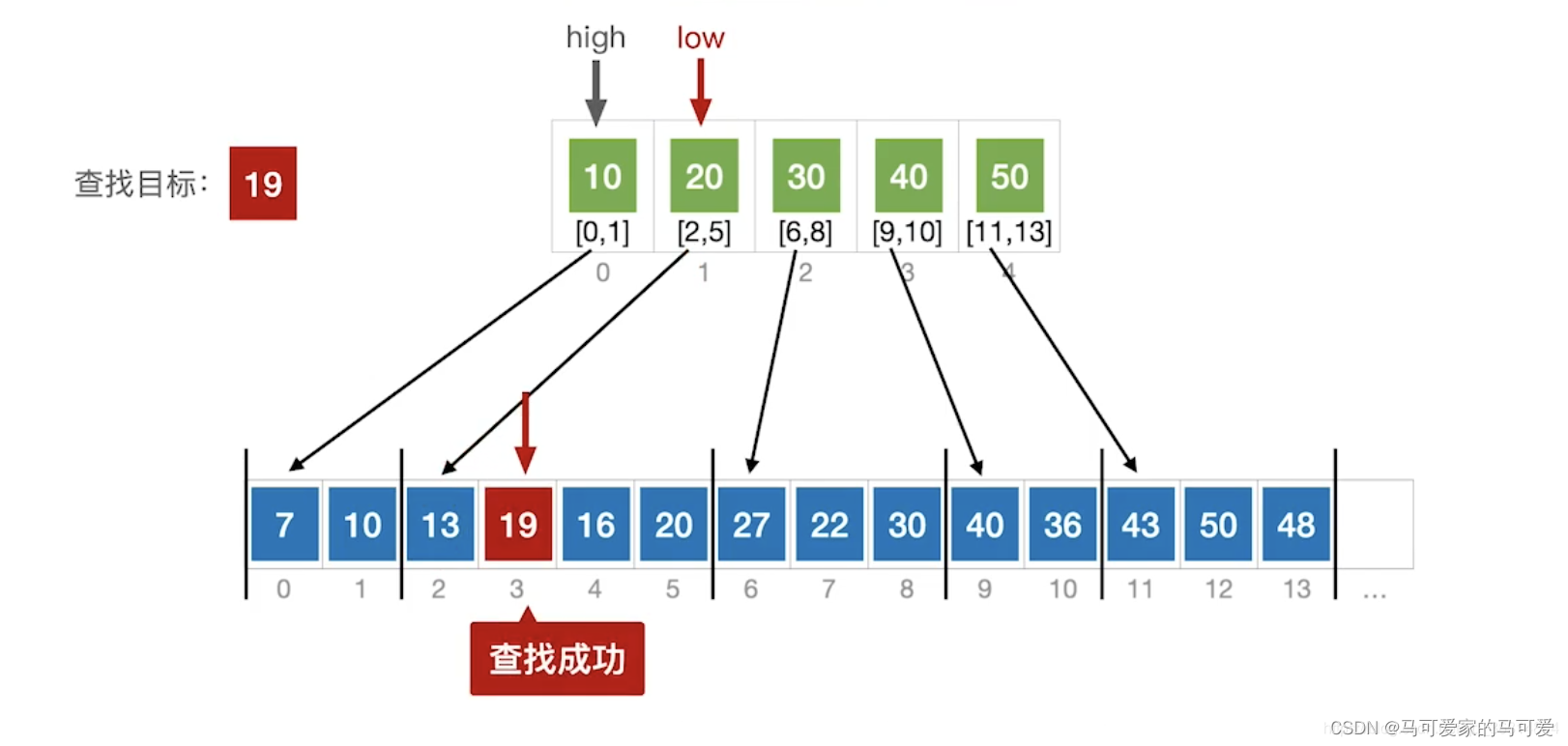
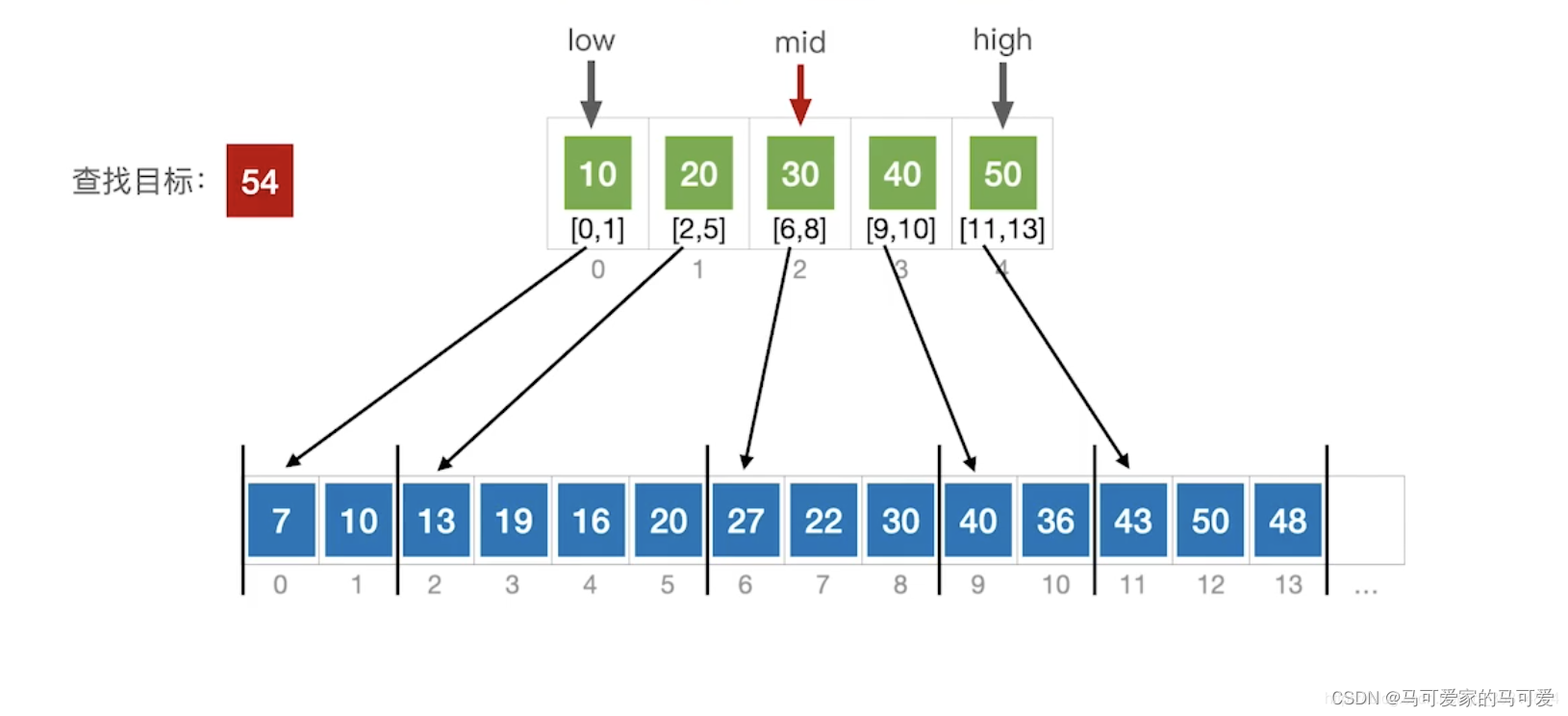
(3)、使用折半查找索引表
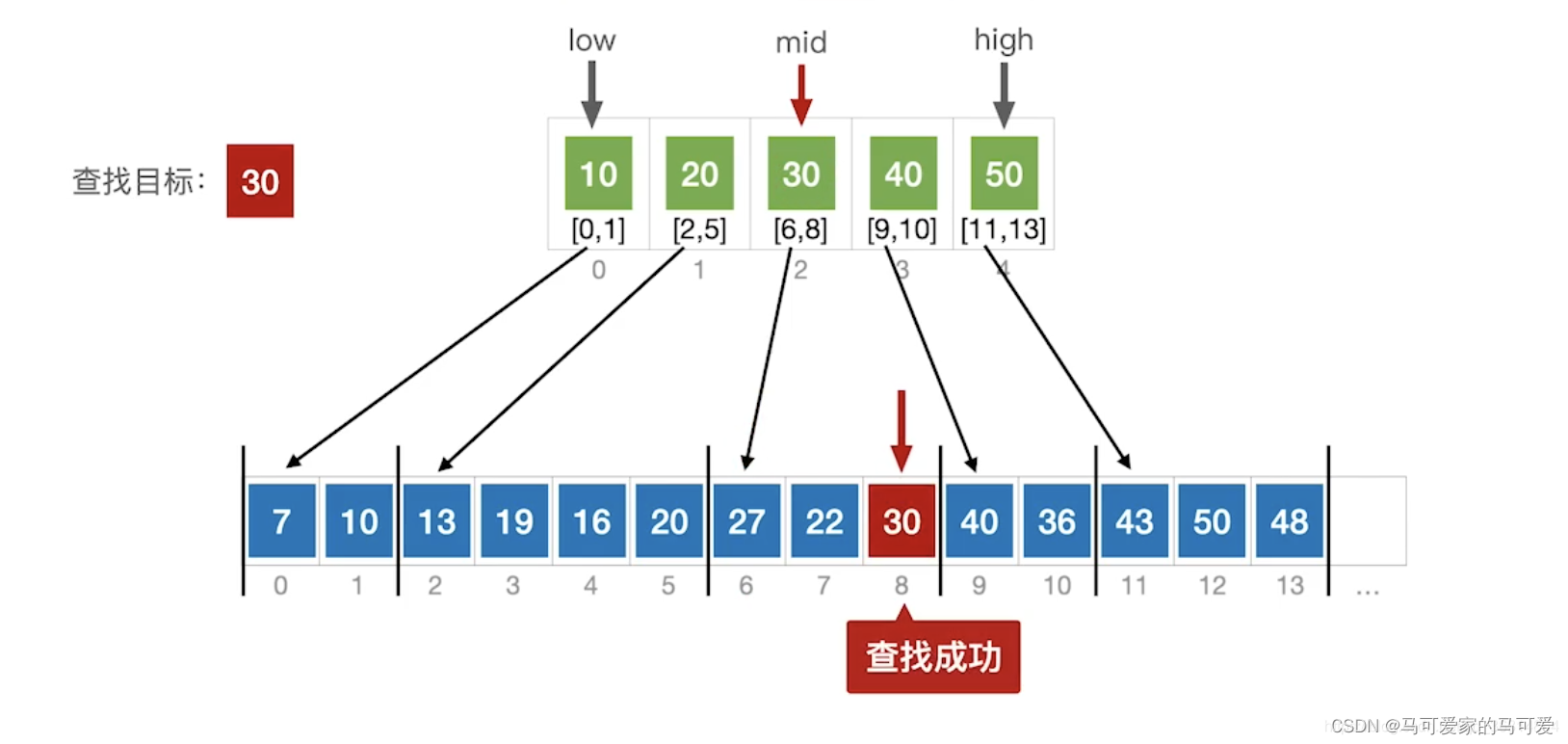
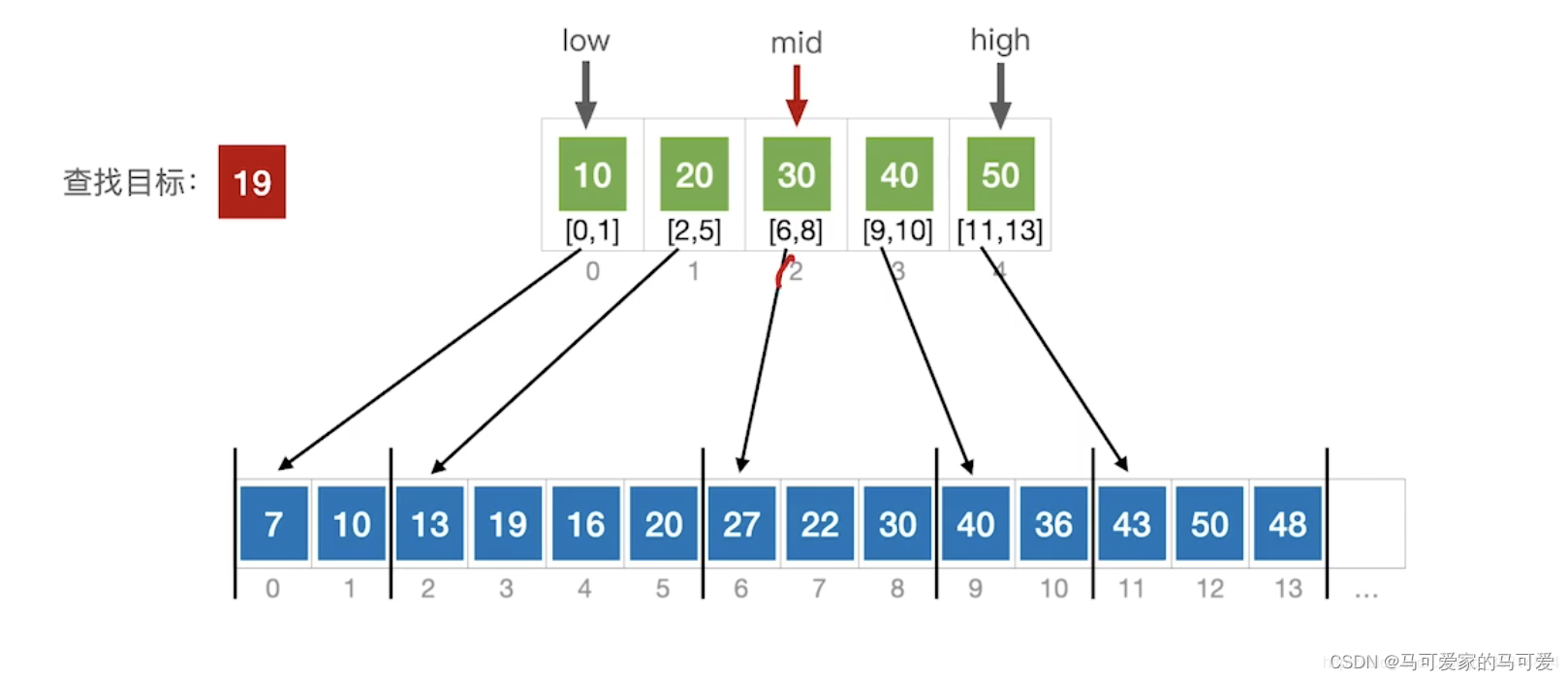
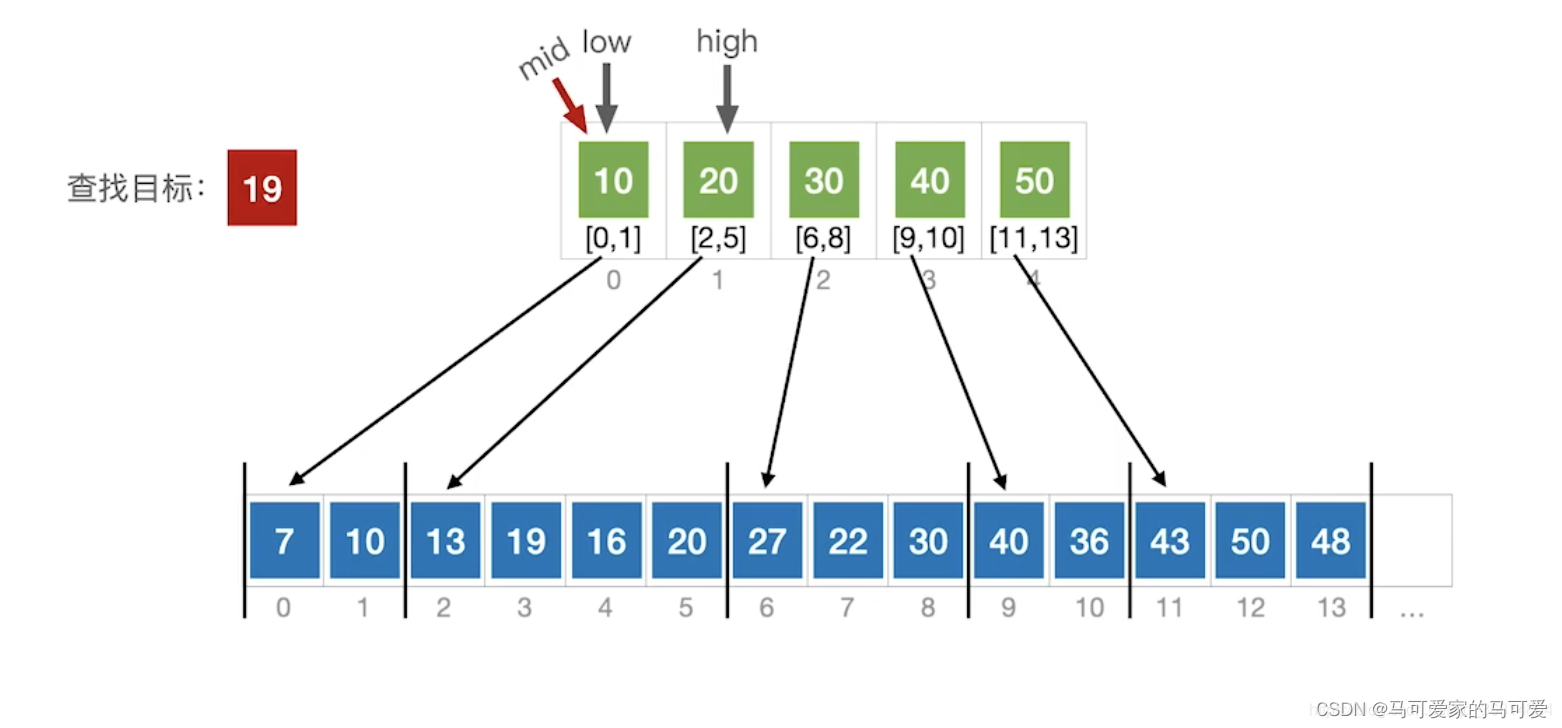
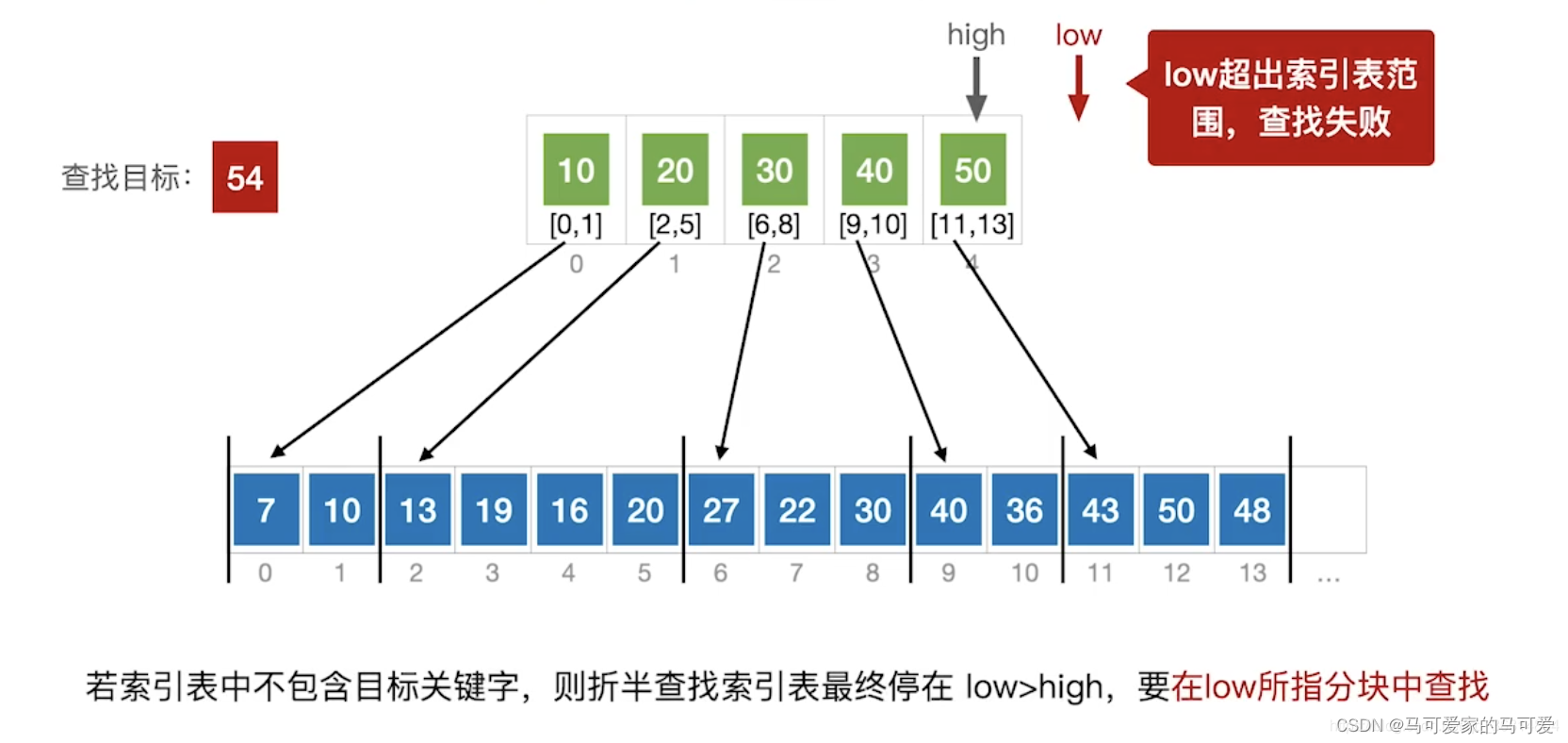
(4)、ASL分析
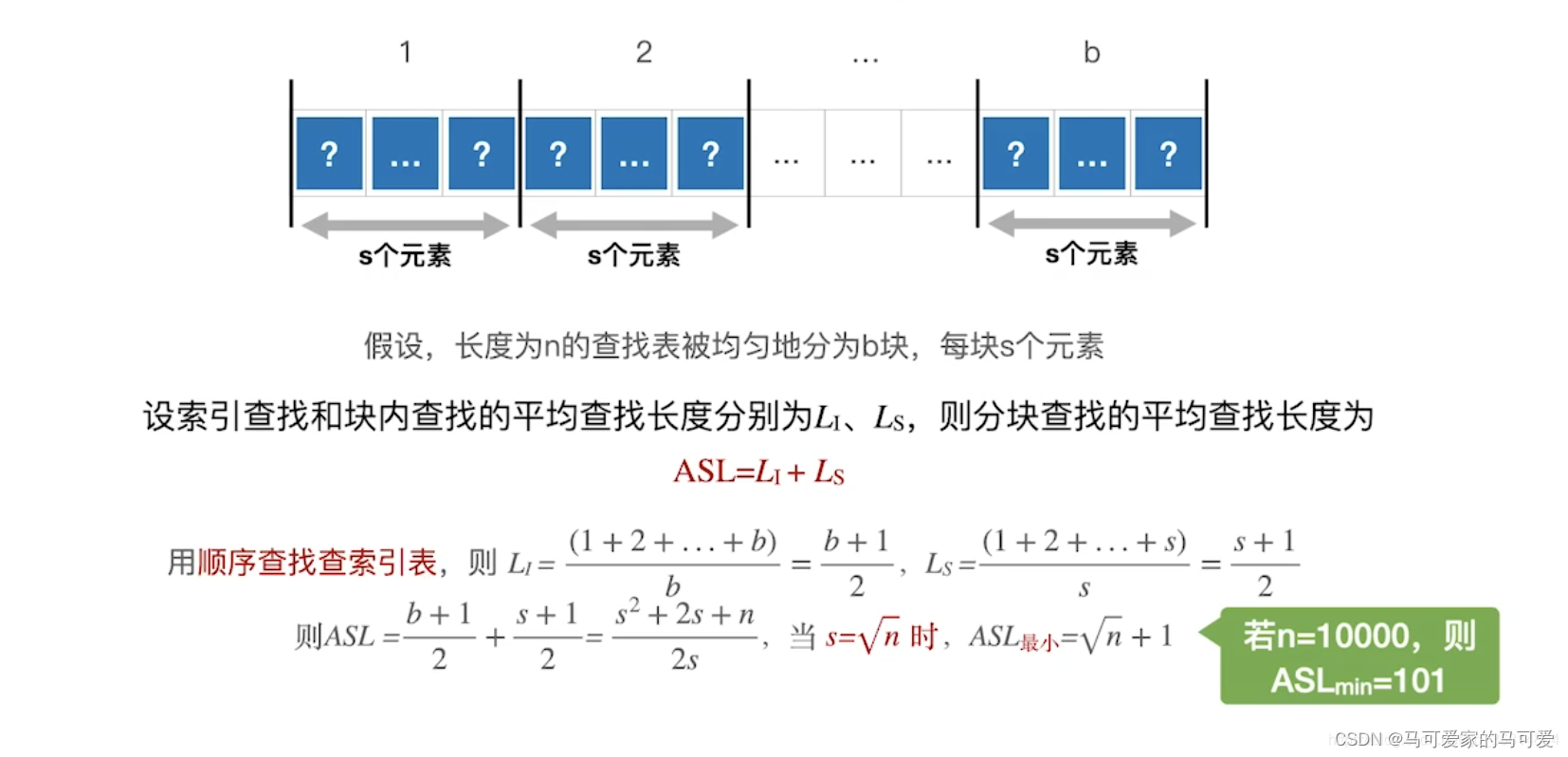
当 s 取根号n的时候,ASLmin = 根号n + 1,这个值比顺序查找有了很大的改进,但是远不及折半查找!
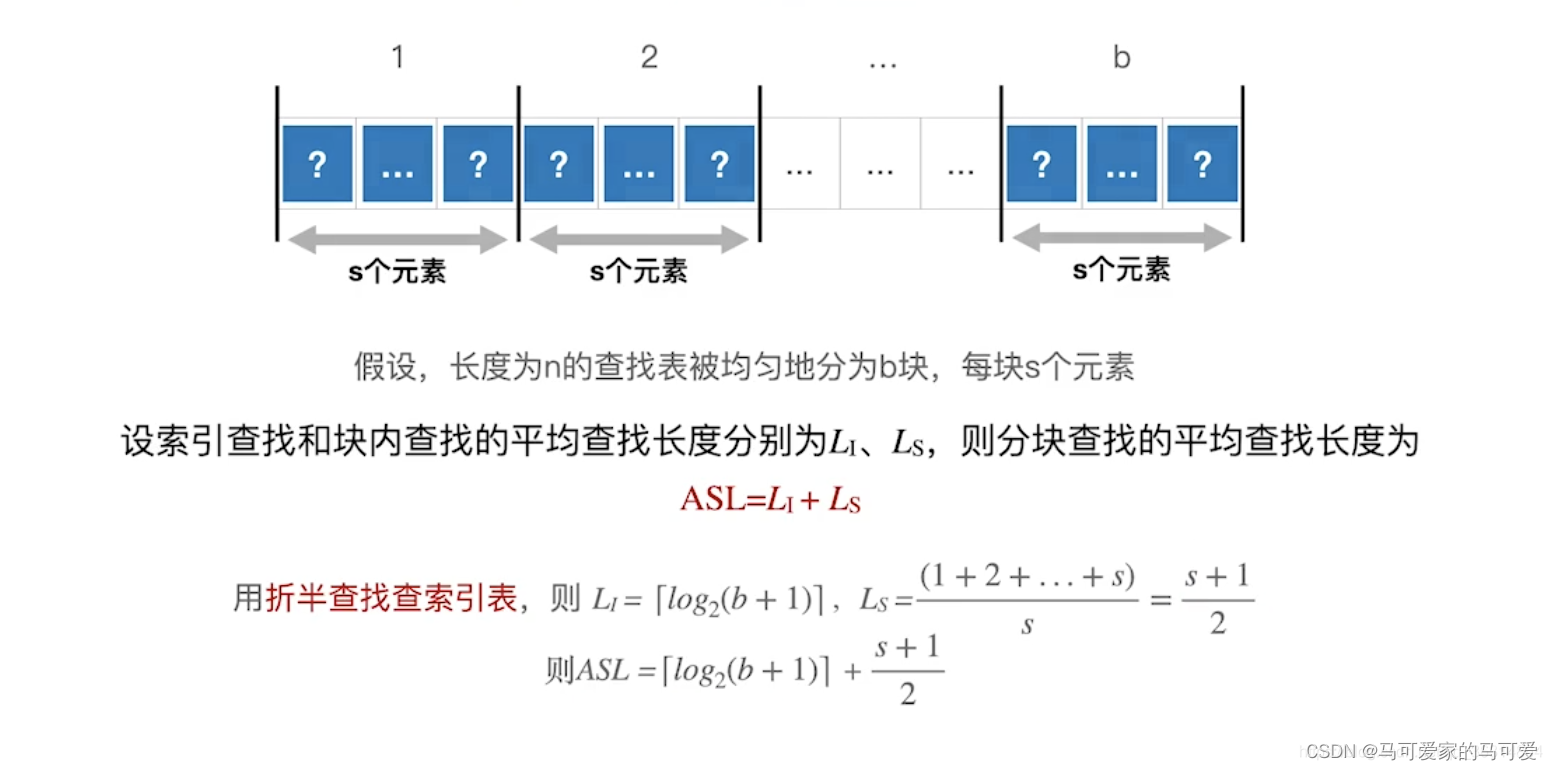
严蔚敏版数据结构与算法中 ASL = log2[n/s + 1] + s/2 = log2[b + 1] + s/2,和王道中有些不同!
(5)、算法分析
在表中插入或者删除数据的时候,只要找到该元素对应的块,就可以在该块内进行插入或者删除操作。由于块内是无序的,故插入或者删除比较容易,无需进行大量的移动。如果线性表既要实现快速查找又要经常插入或者删除的动态变化,则可以使用分块查找,因为块间可以使用折半查找(二分查找),而块内无序可以实现插入或者删除,不需要大量的移动!
边栏推荐
- 跨域解决方案
- 网络安全与元宇宙:找出薄弱环节
- SuperMap支持的国产环境汇总
- Understand the recommendation system in one article: Recall 06: Two-tower model - model structure, training method, the recall model is a late fusion feature, and the sorting model is an early fusion
- 【Unity入门计划】2D游戏中遮挡问题的处理方法&伪透视
- fragment可见性判断
- Live playback including PPT download | Build Online Deep Learning based on Flink & DeepRec
- JZ搜索引擎solr研究-从数据库创建索引
- 树形查找(二叉查找树)
- [Endnote] Word inserts a custom form of Endnote document format
猜你喜欢

软件测试技术之最有效的七大性能测试技术
使用SuperMap iDesktopX数据迁移工具迁移ArcGIS数据
为什么他们选择和AI恋爱?

iNFTnews | 对体育行业和球迷来说,NFT可以带来什么?
![[Redis] Redis installation under Linux](/img/84/7791a87ff976be15b455f6ddc05bf2.png)
[Redis] Redis installation under Linux

“嘀哩哩,等灯等灯”,工厂安全生产的提示音
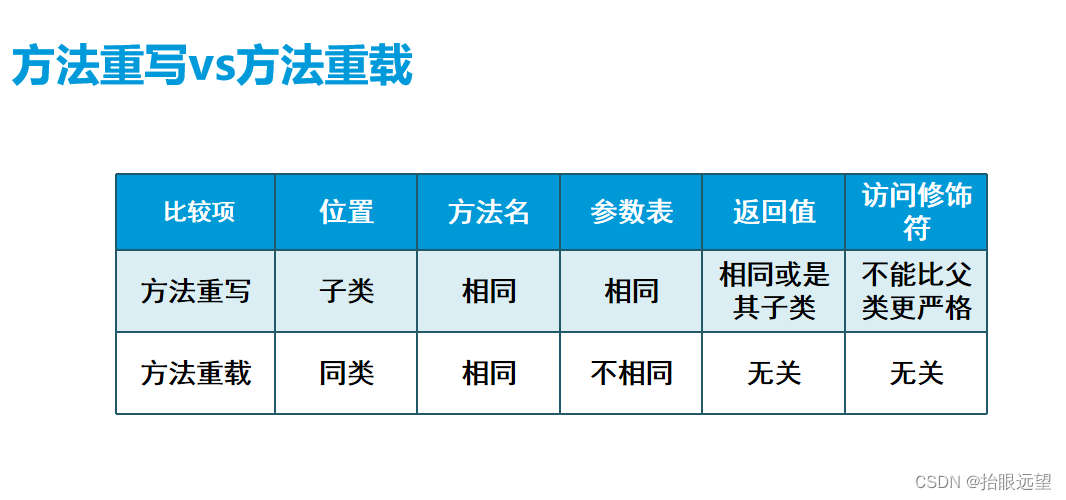
方法重写与Object类
ExcelPatternTool: Excel table-database mutual import tool
英特尔 XDC 2022 精彩回顾:共建开放生态,释放“基建”潜能
KingbaseES V8 GIS data migration solution (2. Introduction to the capabilities of Kingbase GIS)
随机推荐
Jincang database KingbaseES V8 GIS data migration solution (3. Data migration based on ArcGIS platform to KES)
【Endnote】Word插入自定义形式的Endnote文献格式
第09章 性能分析工具的使用【2.索引及调优篇】【MySQL高级】
C language basics -- pointers
iNFTnews | 对体育行业和球迷来说,NFT可以带来什么?
Flink 1.15.1 集群搭建(StandaloneSession)
DDOS攻击真的是无解吗?不!
SuperMap iDesktop.Net之布尔运算求交——修复含拓扑错误复杂模型
Greenplum Database Fault Analysis - Can a Soft Connection Be Made to the Database Base Folder?
Leetcode刷题——22. 括号生成
开篇-开启全新的.NET现代应用开发体验
KingbaseES V8 GIS data migration solution (2. Introduction to the capabilities of Kingbase GIS)
【MySQL series】- Does LIKE query start with % will make the index invalid?
如何逐步执行数据风险评估
STM32使用stm32cubemx LL库系列教程
MySQL3
直播预告|30分钟快速入门!来看可信分布式AI链桨的架构设计
接口自动化测试框架postman tests常用方法
Live preview | 30 minutes started quickly!Look at credible distributed AI chain oar architectural design
树形查找(二叉查找树)