当前位置:网站首页>[combinatorics] Application of exponential generating function (multiple set arrangement problem | different balls in different boxes | derivation of exponential generating function of odd / even sequ
[combinatorics] Application of exponential generating function (multiple set arrangement problem | different balls in different boxes | derivation of exponential generating function of odd / even sequ
2022-07-03 03:05:00 【Programmer community】
List of articles
- Full Permutation formula of multiple sets
- Exponential generating function Deal with the arrangement of multiple sets introduce
- Exponential generating function Deal with the arrangement of multiple sets Formula derivation
- Exponential generating function Handle Finite number string problem
- Exponential generating function Handle n Bit string problem
- Exponential generating function Handle n Bit string problem ( Examination questions )
Full Permutation formula of multiple sets
Given multiset , Yes
k
k
k Elements , Each element
n
i
n_i
ni individual ;
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
 
,
n
k
⋅
a
k
}
S = \{n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k\}
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}
Full Permutation of multiple sets Formula is
n
!
n
1
!
n
2
!
⋯
n
k
!
\cfrac{n!}{n_1! n_2!\cdots n_k!}
n1!n2!⋯nk!n!
among
n
=
n
1
+
n
2
+
n
3
+
⋯
+
n
k
n=n_1 + n_2 + n_3 + \cdots + n_k
n=n1+n2+n3+⋯+nk ;
Exponential generating function Deal with the arrangement of multiple sets introduce
Given multiset , Yes
k
k
k Elements , Each element
n
i
n_i
ni individual ;
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
 
,
n
k
⋅
a
k
}
S = \{n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k\}
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}
But if it's not all arranged , Is to select some of these elements to arrange , You use Exponential generating function ;
Exponential generating function It can deal with the arrangement of multiple sets :
Exponential generating function Deal with the arrangement of multiple sets Formula derivation
Derivation of exponential generating function formula :
① Every element has to find its General
x
k
k
!
\cfrac{x^k}{k!}
k!xk ;
② For the first element
a
1
a_1
a1 It's advisable Number Of The scope is
{
0
,
1
,
2
,
3
,
⋯
 
,
n
1
}
\{0, 1, 2, 3, \cdots , n_1\}
{ 0,1,2,3,⋯,n1} ,
Its exponential generating function is
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
⋯
x
n
1
n
1
!
\cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_1}}{ {n_1}!}
0!x0+1!x1+2!x2+⋯n1!xn1
It is reduced to :
1
+
x
1
!
+
x
2
2
!
+
⋯
x
n
1
n
1
!
1 + \cfrac{x}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_1}}{ {n_1}!}
1+1!x+2!x2+⋯n1!xn1
③ For the second element
a
2
a_2
a2 The number of acceptable Of The scope is
{
0
,
1
,
2
,
3
,
⋯
 
,
n
2
}
\{0, 1, 2, 3, \cdots , n_2\}
{ 0,1,2,3,⋯,n2} ;
Its exponential generating function is
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
⋯
x
n
2
n
2
!
\cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_2}}{ {n_2}!}
0!x0+1!x1+2!x2+⋯n2!xn2
It is reduced to :
1
+
x
1
!
+
x
2
2
!
+
⋯
x
n
2
n
2
!
1 + \cfrac{x}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_2}}{ {n_2}!}
1+1!x+2!x2+⋯n2!xn2
④ For the first
k
k
k Elements
a
k
a_k
ak The number of acceptable Of The scope is
{
0
,
1
,
2
,
3
,
⋯
 
,
n
k
}
\{0, 1, 2, 3, \cdots , n_k\}
{ 0,1,2,3,⋯,nk} ;
Its exponential generating function is
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
⋯
x
n
k
n
k
!
\cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_k}}{ {n_k}!}
0!x0+1!x1+2!x2+⋯nk!xnk
It is reduced to :
1
+
x
1
!
+
x
2
2
!
+
⋯
x
n
k
n
k
!
1 + \cfrac{x}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_k}}{ {n_k}!}
1+1!x+2!x2+⋯nk!xnk
⑤ The final exponential generating function is :
G
e
(
x
)
=
(
1
+
x
1
!
+
x
2
2
!
+
⋯
x
n
1
n
1
!
)
(
1
+
x
1
!
+
x
2
2
!
+
⋯
x
n
2
n
2
!
)
⋯
(
1
+
x
1
!
+
x
2
2
!
+
⋯
x
n
k
n
k
!
)
G_e(x) = (1 + \cfrac{x}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_1}}{ {n_1}!}) (1 + \cfrac{x}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_2}}{ {n_2}!}) \cdots (1 + \cfrac{x}{1!} + \cfrac{x^2}{2!} + \cdots \cfrac{x^{n_k}}{ {n_k}!})
Ge(x)=(1+1!x+2!x2+⋯n1!xn1)(1+1!x+2!x2+⋯n2!xn2)⋯(1+1!x+2!x2+⋯nk!xnk)
Exponential generating function Handle Finite number string problem
subject :
Yes
4
4
4 A digital
1
,
2
,
3
,
4
1, 2,3,4
1,2,3,4 constitute
5
5
5 digit Number of schemes ;
among
1
1
1 Not more than
2
2
2 Time , There must be ;
among
2
2
2 No more than
1
1
1 Time ;
among
3
3
3 The number of occurrences can reach
3
3
3 Time , It's also possible not to appear ;
among
4
4
4 The number of occurrences must be even numbers ;
analysis :
- 1.
1
1
1
1
1 Not more than
2
2
2 Time , There must be , therefore At least there must be
1
1
1 Time , The sequence of its occurrence here is
{
1
,
2
}
\{1, 2\}
{ 1,2} ;
- Its corresponding exponential generating function is :
(
x
1
1
!
+
x
2
2
!
)
(\cfrac{x^1}{1!} + \cfrac{x^2}{2!})
(1!x1+2!x2) ;
1 Number of occurrences :
- Its corresponding exponential generating function is :
- 2.
2
2
2
2
2 Not more than
1
1
1 Time , The sequence of its occurrence here is
{
0
,
1
}
\{0, 1\}
{ 0,1} ;
- Its corresponding exponential generating function is :
(
x
0
0
!
+
x
1
1
!
)
( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} )
(0!x0+1!x1) ;
2 Number of occurrences :
- Its corresponding exponential generating function is :
- 3.
3
3
3
3
3 The number of occurrences can reach
3
3
3 Time , Can not appear , The sequence of its occurrence here is
{
0
,
1
,
2
,
3
}
\{0, 1, 2, 3\}
{ 0,1,2,3} ;
- Its corresponding exponential generating function is :
(
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
)
( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} )
(0!x0+1!x1+2!x2+3!x3) ;
3 Number of occurrences :
- Its corresponding exponential generating function is :
- 4.
4
4
4
4
4 The number of occurrences is even , The sequence of its occurrence here is
{
0
,
2
,
4
}
\{0, 2, 4\}
{ 0,2,4} ;
- Its corresponding exponential generating function is :
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
)
( \cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} )
(0!x0+2!x2+4!x4) ;
4 Number of occurrences :
- Its corresponding exponential generating function is :
Explain :
① Write its corresponding generating function : Here is the arrangement , Therefore, the general term of the generating function must be divided by
k
!
k!
k! ;
G
e
(
x
)
=
(
x
1
1
!
+
x
2
2
!
)
(
x
0
0
!
+
x
1
1
!
)
(
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
)
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
)
=
(
x
+
x
2
2
!
)
(
1
+
x
)
(
1
+
x
+
x
2
2
!
+
x
3
3
!
)
(
1
+
x
2
2
!
+
x
4
4
!
)
G_e(x) = (\cfrac{x^1}{1!} + \cfrac{x^2}{2!}) ( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} ) ( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} ) ( \cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} )\\ = ( x + \cfrac{x^2}{2!}) ( 1+ x) ( 1 + x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} ) ( 1 + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} )
Ge(x)=(1!x1+2!x2)(0!x0+1!x1)(0!x0+1!x1+2!x2+3!x3)(0!x0+2!x2+4!x4)=(x+2!x2)(1+x)(1+x+2!x2+3!x3)(1+2!x2+4!x4)
② Expand the above formula :
G
e
(
x
)
=
(
x
+
3
2
x
2
+
1
2
x
3
)
(
1
+
x
+
x
2
+
2
3
x
3
+
7
24
x
4
+
1
8
x
5
+
1
48
x
6
+
1
144
x
7
)
=
x
+
5
2
x
2
+
3
x
3
+
8
3
x
4
+
43
24
x
5
+
43
48
x
6
+
17
48
x
7
+
1
288
x
8
+
1
48
x
9
+
1
288
x
10
G_e(x) = (x + \cfrac{3}{2} x^2 + \cfrac{1}{2} x^3) (1 + x + x^2 + \cfrac{2}{3}x^3+ \cfrac{7}{24}x^4 + \cfrac{1}{8}x^5 + \cfrac{1}{48}x^6 + \cfrac{1}{144}x^7) \\ = x + \cfrac{5}{2}x^2 + 3x^3 + \cfrac{8}{3}x^4 + \cfrac{43}{24}x^5 + \cfrac{43}{48}x^6 + \cfrac{17}{48}x^7 + \cfrac{1}{288}x^8 + \cfrac{1}{48}x^9 + \cfrac{1}{288}x^{10}
Ge(x)=(x+23x2+21x3)(1+x+x2+32x3+247x4+81x5+481x6+1441x7)=x+25x2+3x3+38x4+2443x5+4843x6+4817x7+2881x8+481x9+2881x10
③ Put the above formula in Of
43
24
x
5
\cfrac{43}{24}x^5
2443x5 term Convert to
x
k
k
!
\cfrac{x^k}{k!}
k!xk In the form of :
43
×
5
!
24
×
5
!
x
5
=
43
×
5
!
24
×
x
5
5
!
=
43
×
5
×
4
×
3
×
2
24
×
x
5
5
!
=
215
×
x
5
5
!
\cfrac{43 \times 5!}{24 \times 5!}x^5 =\cfrac{43 \times 5!}{24} \times \cfrac{x^5}{5!} =\cfrac{43 \times 5 \times 4 \times 3 \times 2}{24} \times \cfrac{x^5}{5!} = 215 \times \cfrac{x^5}{5!}
24×5!43×5!x5=2443×5!×5!x5=2443×5×4×3×2×5!x5=215×5!x5
④ The above calculation results
x
5
5
!
\cfrac{x^5}{5!}
5!x5 Of The coefficient is
215
215
215 ; therefore Four Numbers constitute
5
5
5 The number of schemes with digits is
215
215
215 individual ;
Exponential generating function Handle n Bit string problem
subject : seek
1
,
3
,
5
,
7
,
9
1,3,5,7,9
1,3,5,7,9 Five numbers , form
n
n
n Number of schemes with digits , At the same time, the following requirements should be met ;
3
,
7
3,7
3,7 Here is even numbers ;
1
,
5
,
9
1,5,9
1,5,9 There is no limit to the number of occurrences ;
analysis : Is equivalent to
n
n
n Put a different ball into
1
,
3
,
5
,
7
,
9
1,3,5,7,9
1,3,5,7,9 Five boxes , The number of balls in each box Number of schemes ;
3
,
7
3,7
3,7 Occurrence analysis : It can only appear Even number of times , namely The number of occurrences is a sequence
{
0
,
2
,
4
,
⋯
 }
\{0, 2, 4, \cdots\}
{ 0,2,4,⋯} ;
- The corresponding exponential generating function term is :
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
+
…
 )
(\cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \dots)
(0!x0+2!x2+4!x4+…) ;
- The corresponding exponential generating function term is :
1
,
5
,
9
1,5,9
1,5,9 Occurrence analysis : There is no limit to the number of times it appears , Then the sequence of occurrences is
0
,
1
,
2
,
⋯
{0, 1, 2, \cdots}
0,1,2,⋯
- The corresponding exponential generating function term is :
(
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
⋯
 )
=
e
x
( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cdots ) = e^x
(0!x0+1!x1+2!x2+⋯)=ex ;
- The corresponding exponential generating function term is :
Explain :
① Write the corresponding Exponential generating function :
G
e
(
x
)
=
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
+
⋯
 
)
2
(
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
3
G_e(x) = ( \cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots )^2 ( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots)^3
Ge(x)=(0!x0+2!x2+4!x4+⋯)2(0!x0+1!x1+2!x2+3!x3+⋯)3
② Number of occurrences Normal natural number Sequence
{
0
,
1
,
2
,
3
,
4
,
⋯
 
}
\{ 0, 1, 2, 3, 4, \cdots\}
{ 0,1,2,3,4,⋯} Calculation of exponential generating function :
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
=
∑
k
=
0
∞
1
⋅
x
k
k
!
=
e
x
\begin{array}{lcl} & \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots\\ \\ = & 1+ x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots\\ \\ =& \sum_{k=0}^{\infty} 1 \cdot \cfrac{x^k}{k!} \\ = & e^x \end{array}
===0!x0+1!x1+2!x2+3!x3+⋯1+x+2!x2+3!x3+⋯∑k=0∞1⋅k!xkex
② appear Even number of times Sequence
{
0
,
2
,
4
,
6
,
⋯
 
}
\{0 , 2, 4, 6 , \cdots\}
{ 0,2,4,6,⋯} Calculation of exponential generating function : Eliminate odd items , Leave even items ;
Two formulas are known :
e
x
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
e^x = 1+ x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots
ex=1+x+2!x2+3!x3+⋯
( All terms of this formula are positive )
e
−
x
=
1
−
x
+
x
2
2
!
−
x
3
3
!
+
⋯
e^{-x} = 1 - x + \cfrac{x^2}{2!} - \cfrac{x^3}{3!} + \cdots
e−x=1−x+2!x2−3!x3+⋯
( All even terms of the formula It's all positive , All odd directions are negative )
Add the two formulas :
e
x
+
e
−
x
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
+
1
−
x
+
x
2
2
!
−
x
3
3
!
+
⋯
=
1
×
2
+
x
2
2
!
×
2
+
x
4
4
!
×
2
+
⋯
\begin{array}{lcl}e^x + e^{-x} & = & 1 + x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots \\ \\ && +1 - x + \cfrac{x^2}{2!} - \cfrac{x^3}{3!} + \cdots \\ \\ & = & 1 \times 2 + \cfrac{x^2}{2!} \times 2 + \cfrac{x^4}{4!} \times 2 + \cdots \end{array}
ex+e−x==1+x+2!x2+3!x3+⋯+1−x+2!x2−3!x3+⋯1×2+2!x2×2+4!x4×2+⋯
( The result is even numbers Sequence Exponential generating function 2 times )
Even sequence generating function calculation :
1
+
x
2
2
!
+
x
4
4
!
+
⋯
=
1
2
(
e
x
+
e
−
x
)
1 + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots = \cfrac{1}{2} (e^x + e^{-x})
1+2!x2+4!x4+⋯=21(ex+e−x)
③ take ① ② The result of is substituted into the exponential generating function :
G
e
(
x
)
=
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
+
⋯
 
)
2
(
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
3
=
(
1
2
(
e
x
+
e
−
x
)
)
2
(
e
x
)
3
=
1
4
(
2
e
x
e
−
x
+
e
2
x
+
e
−
2
x
)
e
3
x
=
1
4
(
2
e
3
x
+
e
5
x
+
e
x
)
=
1
4
(
∑
n
=
0
∞
5
n
n
!
x
n
+
2
∑
n
=
0
∞
3
n
n
!
x
n
+
∑
n
=
0
∞
1
n
!
x
n
)
=
1
4
∑
n
=
0
∞
(
5
n
+
2
⋅
3
n
+
1
)
x
n
n
!
\begin{array}{lcl}G_e(x) &=& ( \cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots )^2 ( \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots)^3\\ \\ &=& ( \cfrac{1}{2} (e^x + e^{-x}))^2 (e^x)^3 \\ &=& \cfrac{1}{4}( 2 e^x e^{-x} + e^{2x} + e^{-2x} ) e^{3x} \\ &=& \cfrac{1}{4}( 2 e^{3x} + e^{5x} + e^{x} ) \\ &=& \cfrac{1}{4} ( \sum_{n=0}^{\infty} \cfrac{5^n}{n!} x^n + 2\sum_{n=0}^{\infty} \cfrac{3^n}{n!} x^n + \sum_{n=0}^{\infty} \cfrac{1}{n!} x^n ) \\ &=& \cfrac{1}{4} \sum_{n=0}^{\infty} ( 5^n + 2 \cdot 3^n + 1 ) \cfrac{x^n}{n!} \\ \end{array}
Ge(x)======(0!x0+2!x2+4!x4+⋯)2(0!x0+1!x1+2!x2+3!x3+⋯)3(21(ex+e−x))2(ex)341(2exe−x+e2x+e−2x)e3x41(2e3x+e5x+ex)41(∑n=0∞n!5nxn+2∑n=0∞n!3nxn+∑n=0∞n!1xn)41∑n=0∞(5n+2⋅3n+1)n!xn
thus , You can get
x
n
n
!
\cfrac{x^n}{n!}
n!xn The coefficient of is
1
4
(
5
n
+
2
⋅
3
n
+
1
)
\cfrac{1}{4} ( 5^n + 2 \cdot 3^n + 1 )
41(5n+2⋅3n+1)
④
5
5
5 The digits are composed as required
n
n
n Number of digits, number of schemes yes
1
4
(
5
n
+
2
⋅
3
n
+
1
)
\cfrac{1}{4} ( 5^n + 2 \cdot 3^n + 1 )
41(5n+2⋅3n+1) Kind of ;
Exponential generating function Handle n Bit string problem ( Examination questions )
subject : hold
n
n
n Numbered balls , Put in
3
3
3 In a different box , At the same time, the following requirements should be met ;
The first
1
1
1 Put at least one box ;
The first
2
2
2 Put an odd number of boxes ;
The first
3
3
3 Put an even number of boxes ;
analysis :
- The first
1
1
1 Analysis of the number of balls in a box : At least one , It puts the ball Number Sequence is
{
1
,
2
,
3
,
⋯
 }
\{1, 2, 3, \cdots\}
- The first
1
1
1 Boxes Of Release sequence Corresponding Exponential generating function :
(
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
 )
(\cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots)
(1!x1+2!x2+3!x3+⋯)
{ 1,2,3,⋯}
- The first
- The first
2
2
2 Analysis of the number of balls in a box : Put an odd number of balls , It puts the ball Number Sequence is
{
1
,
3
,
5
,
⋯
 }
\{1, 3, 5, \cdots\}
- The first
2
2
2 Boxes Of Release sequence Corresponding Exponential generating function :
(
x
1
1
!
+
x
3
3
!
+
x
5
5
!
+
⋯
 )
(\cfrac{x^1}{1!} + \cfrac{x^3}{3!} + \cfrac{x^5}{5!} + \cdots)
(1!x1+3!x3+5!x5+⋯)
{ 1,3,5,⋯}
- The first
- The first
3
3
3 Analysis of the number of balls in a box : Put an even number of balls , It puts the ball Number Sequence is
{
2
,
4
,
6
,
⋯
 }
\{2, 4, 6, \cdots\}
- The first
3
3
3 Boxes Of Release sequence Corresponding Exponential generating function :
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
+
⋯
 )
(\cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots)
(0!x0+2!x2+4!x4+⋯)
{ 2,4,6,⋯}
- The first
Explain :
① Write the generating function :
G
e
(
x
)
=
(
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
(
x
1
1
!
+
x
3
3
!
+
x
5
5
!
+
⋯
 
)
(
x
0
0
!
+
x
2
2
!
+
x
4
4
!
+
⋯
 
)
=
(
x
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
(
x
+
x
3
3
!
+
x
5
5
!
+
⋯
 
)
(
1
+
x
2
2
!
+
x
4
4
!
+
⋯
 
)
\begin{array}{lcl}\\ G_e(x) &=& (\cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots) ( \cfrac{x^1}{1!} + \cfrac{x^3}{3!} + \cfrac{x^5}{5!} + \cdots ) ( \cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots )\\ \\ &=& ( x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots ) ( x + \cfrac{x^3}{3!} + \cfrac{x^5}{5!} + \cdots ) ( 1 + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots ) \\ \end{array}
Ge(x)==(1!x1+2!x2+3!x3+⋯)(1!x1+3!x3+5!x5+⋯)(0!x0+2!x2+4!x4+⋯)(x+2!x2+3!x3+⋯)(x+3!x3+5!x5+⋯)(1+2!x2+4!x4+⋯)
② Calculation The first
1
1
1 individual The box Of Exponential generating function term ( except
0
0
0 Outer sequence ) :
We know the formula :
e
x
=
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
\begin{array}{lcl}e^x &=& \cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots\\ \\ &=& 1 + x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots \\ \end{array}
ex==0!x0+1!x1+2!x2+3!x3+⋯1+x+2!x2+3!x3+⋯
e
−
x
=
x
0
0
!
−
x
1
1
!
+
x
2
2
!
−
x
3
3
!
+
⋯
=
1
−
x
+
x
2
2
!
−
x
3
3
!
+
⋯
\begin{array}{lcl}e^{-x} &=& \cfrac{x^0}{0!} - \cfrac{x^1}{1!} + \cfrac{x^2}{2!} - \cfrac{x^3}{3!} + \cdots\\ \\ &=& 1 - x + \cfrac{x^2}{2!} - \cfrac{x^3}{3!} + \cdots \\ \end{array}
e−x==0!x0−1!x1+2!x2−3!x3+⋯1−x+2!x2−3!x3+⋯
The exponential generating function corresponding to the first box :
x
+
x
2
2
!
+
x
3
3
!
+
⋯
=
e
x
−
1
\begin{array}{lcl}\\ x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots = e^x-1 \end{array}
x+2!x2+3!x3+⋯=ex−1
③ Calculation The first
2
2
2 individual The box Of Exponential generating function term ( Odd sequence ) :
e
x
−
e
−
x
=
(
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
−
(
1
−
x
+
x
2
2
!
−
x
3
3
!
+
⋯
 
)
=
2
(
x
+
x
3
3
!
+
x
5
5
!
+
⋯
 
)
\begin{array}{lcl}\\ e^x - e^{-x} &=& (1 + x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots) - (1 - x + \cfrac{x^2}{2!} - \cfrac{x^3}{3!} + \cdots) \\ &=& 2 ( x + \cfrac{x^3}{3!} + \cfrac{x^5}{5!} + \cdots) \\ \end{array}
ex−e−x==(1+x+2!x2+3!x3+⋯)−(1−x+2!x2−3!x3+⋯)2(x+3!x3+5!x5+⋯)
So odd sequence Corresponding exponential generating function yes :
x
+
x
3
3
!
+
x
5
5
!
+
⋯
=
e
x
−
e
−
x
2
x + \cfrac{x^3}{3!} + \cfrac{x^5}{5!} + \cdots = \cfrac{e^x - e^{-x}}{2}
x+3!x3+5!x5+⋯=2ex−e−x
④ Calculation The first
3
3
3 individual The box Of Exponential generating function term ( Even sequence ) :
e
x
+
e
−
x
=
(
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
+
(
1
−
x
+
x
2
2
!
−
x
3
3
!
+
⋯
 
)
=
2
(
0
+
x
2
2
!
+
x
4
4
!
+
⋯
 
)
\begin{array}{lcl}\\ e^x + e^{-x} &=& (1 + x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots) + (1 - x + \cfrac{x^2}{2!} - \cfrac{x^3}{3!} + \cdots) \\ &=& 2 ( 0 + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots) \\ \end{array}
ex+e−x==(1+x+2!x2+3!x3+⋯)+(1−x+2!x2−3!x3+⋯)2(0+2!x2+4!x4+⋯)
So odd sequence Corresponding exponential generating function yes :
1
+
x
2
2
!
+
x
4
4
!
+
⋯
=
e
x
+
e
−
x
2
1 + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots = \cfrac{e^x + e^{-x}}{2}
1+2!x2+4!x4+⋯=2ex+e−x
⑤ take ② ③ ④ result Plug in Exponential generating function :
G
e
(
x
)
=
(
x
+
x
2
2
!
+
x
3
3
!
+
⋯
 
)
(
x
+
x
3
3
!
+
x
5
5
!
+
⋯
 
)
(
1
+
x
2
2
!
+
x
4
4
!
+
⋯
 
)
=
(
e
x
−
1
)
(
e
x
−
e
−
x
2
)
(
e
x
+
e
−
x
2
)
=
1
4
(
e
x
−
1
)
(
(
e
x
)
2
−
(
e
−
x
)
2
)
=
1
4
(
e
x
−
1
)
(
e
2
x
−
e
−
2
x
)
=
1
4
(
e
x
e
2
x
−
e
x
e
−
2
x
−
e
2
x
+
e
−
2
x
)
=
1
4
(
e
3
x
−
e
−
x
−
e
2
x
+
e
−
2
x
)
=
1
4
(
∑
n
=
0
∞
x
n
n
!
3
n
−
∑
n
=
0
∞
x
n
n
!
(
−
1
)
n
−
∑
n
=
0
∞
x
n
n
!
2
n
+
∑
n
=
0
∞
x
n
n
!
(
−
2
)
n
)
=
∑
n
=
0
∞
x
n
n
!
(
1
4
(
3
n
−
(
−
1
)
n
−
2
n
+
(
−
2
)
n
)
)
\begin{array}{lcl}\\ G_e(x) &=& ( x + \cfrac{x^2}{2!} + \cfrac{x^3}{3!} + \cdots ) ( x + \cfrac{x^3}{3!} + \cfrac{x^5}{5!} + \cdots ) ( 1 + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots )\\ \\ \\ &=& ( e^x - 1) ( \cfrac{e^x - e^{-x}}{2} ) ( \cfrac{e^x + e^{-x}}{2} ) \\ \\ &=& \cfrac{1}{4} (e^x - 1) ( (e^x)^2 - (e^{-x})^2 ) \\ \\ &=& \cfrac{1}{4} (e^x - 1) ( e^{2x} - e^{-2x} ) \\ \\ &=& \cfrac{1}{4} ( e^x e^{2x} - e^x e^{-2x} - e^{2x} + e^{-2x} ) \\ \\ &=& \cfrac{1}{4} (e^{3x} - e^{-x} - e^{2x} + e{-2x} ) \\ \\ &=& \cfrac{1}{4} ( \sum_{n=0}^{\infty}\cfrac{x^n}{n!} 3^n - \sum_{n=0}^{\infty}\cfrac{x^n}{n!} (-1)^n - \sum_{n=0}^{\infty}\cfrac{x^n}{n!} 2^n + \sum_{n=0}^{\infty}\cfrac{x^n}{n!} (-2)^n) \\ \\ &=& \sum_{n=0}^{\infty}\cfrac{x^n}{n!} ( \cfrac{1}{4} ( 3^n - (-1)^n - 2^n + (-2)^n) ) \\ \\ \end{array}
Ge(x)========(x+2!x2+3!x3+⋯)(x+3!x3+5!x5+⋯)(1+2!x2+4!x4+⋯)(ex−1)(2ex−e−x)(2ex+e−x)41(ex−1)((ex)2−(e−x)2)41(ex−1)(e2x−e−2x)41(exe2x−exe−2x−e2x+e−2x)41(e3x−e−x−e2x+e−2x)41(∑n=0∞n!xn3n−∑n=0∞n!xn(−1)n−∑n=0∞n!xn2n+∑n=0∞n!xn(−2)n)∑n=0∞n!xn(41(3n−(−1)n−2n+(−2)n))
thus , You can see
x
n
n
!
\cfrac{x^n}{n!}
n!xn The coefficient before is
1
4
(
3
n
−
(
−
1
)
n
−
2
n
+
(
−
2
)
n
)
\cfrac{1}{4} ( 3^n - (-1)^n - 2^n + (-2)^n)
41(3n−(−1)n−2n+(−2)n) ;
⑥ The final result is calculated :
Based on the above calculation ,
x
n
n
!
\cfrac{x^n}{n!}
n!xn The coefficient before is
1
4
(
3
n
−
(
−
1
)
n
−
2
n
+
(
−
2
)
n
)
\cfrac{1}{4} ( 3^n - (-1)^n - 2^n + (-2)^n)
41(3n−(−1)n−2n+(−2)n) , So the corresponding
n
n
n Numbered balls Put in 3 In different boxes , The number of schemes satisfying a series of conditions is
1
4
(
3
n
−
(
−
1
)
n
−
2
n
+
(
−
2
)
n
)
\cfrac{1}{4} ( 3^n - (-1)^n - 2^n + (-2)^n)
41(3n−(−1)n−2n+(−2)n) ;
边栏推荐
- 左值右指解释的比较好的
- I2C 子系統(四):I2C debug
- Variable declarations following if statements
- open file in 'w' mode: IOError: [Errno 2] No such file or directory
- Opengauss database development and debugging tool guide
- Left connection, inner connection
- ASP. Net core 6 framework unveiling example demonstration [02]: application development based on routing, MVC and grpc
- Thunderbolt Chrome extension caused the data returned by the server JS parsing page data exception
- I2C subsystem (IV): I2C debug
- What does it mean when lambda is not entered?
猜你喜欢

用docker 连接mysql的过程
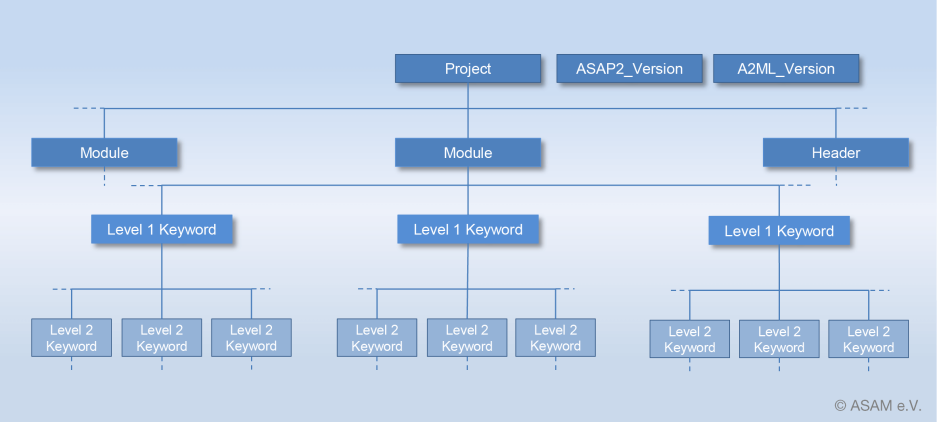
A2L file parsing based on CAN bus (2)
From C to capable -- use the pointer as a function parameter to find out whether the string is a palindrome character
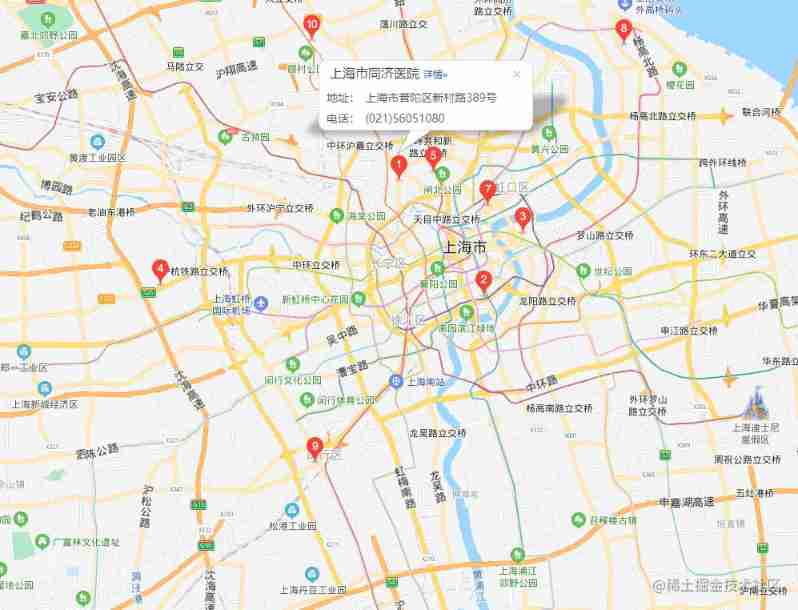
Baidu map - surrounding search

Spark on yarn资源优化思路笔记
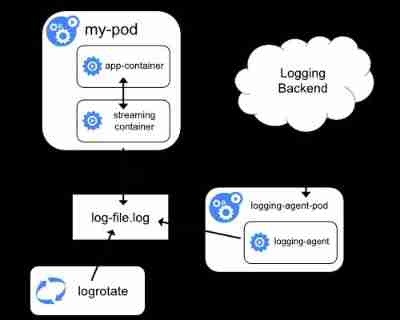
Kubernetes cluster log and efk architecture log scheme

Do you really understand relays?
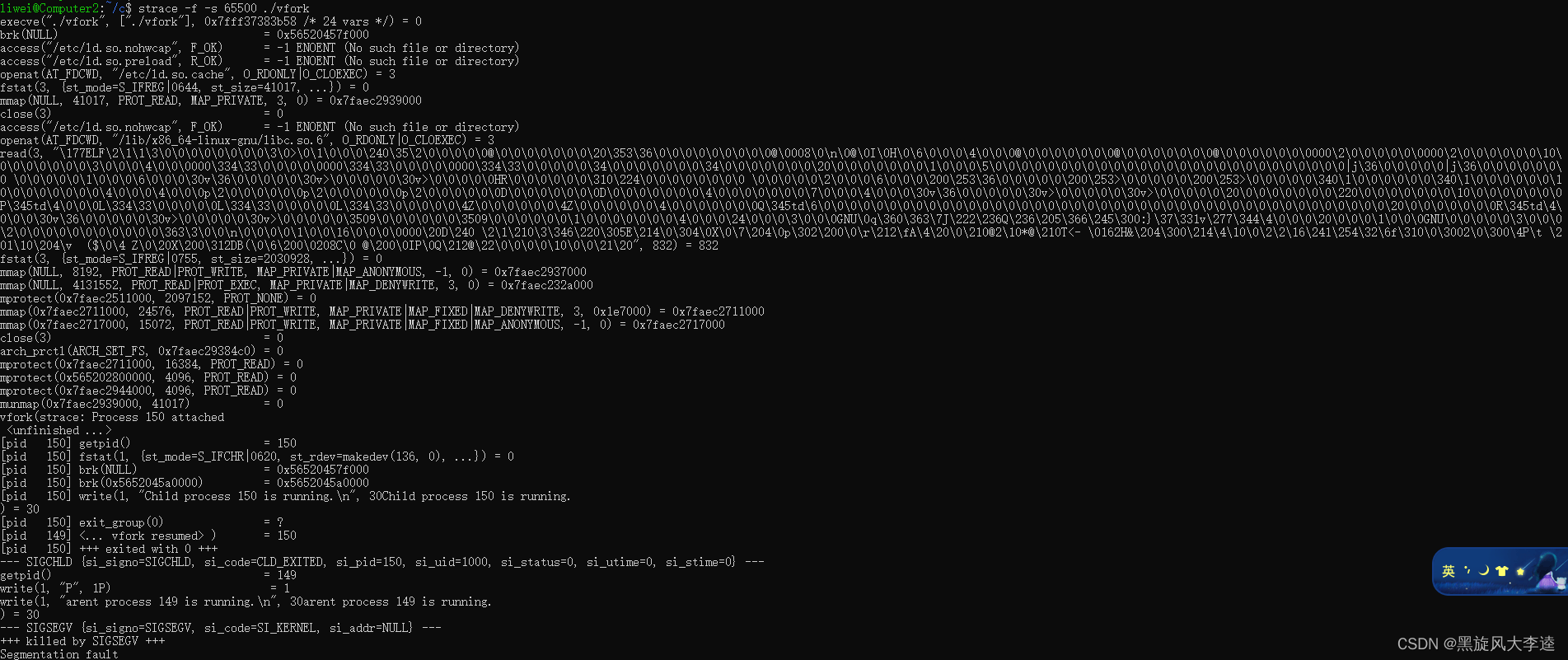
vfork执行时出现Segmentation fault

MySql实战45讲【SQL查询和更新执行流程】

超好用的日志库 logzero
随机推荐
Can netstat still play like this?
Getting started | jetpack hilt dependency injection framework
SqlServer行转列PIVOT
Spark on yarn资源优化思路笔记
Do you really understand relays?
yii2 中andWhere多个or查询 orm条件
Are there any recommended term life insurance products? I want to buy a term life insurance.
[leectode 2022.2.15] lucky numbers in the matrix
Force deduction ----- the minimum path cost in the grid
Andwhere multiple or query ORM conditions in yii2
MySQL practice 45 [global lock and table lock]
敏捷认证(Professional Scrum Master)模拟练习题
I2C 子系统(四):I2C debug
[principles of multithreading and high concurrency: 1_cpu multi-level cache model]
Today, it's time to copy the bottom!
Deep learning: multi-layer perceptron and XOR problem (pytoch Implementation)
用docker 連接mysql的過程
JMeter performance test JDBC request (query database to obtain database data) use "suggestions collection"
SQL server queries the table structure of the specified table
[fluent] futurebuilder asynchronous programming (futurebuilder construction method | asyncsnapshot asynchronous calculation)