【动态规划--01背包】HJ16 购物单

题目描述

王强决定把年终奖用于购物，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

如果要买归类为附件的物品，必须先买该附件所属的主件，且每件物品只能购买一次。
每个主件可以有 0 个、 1 个或 2 个附件。附件不再有从属于自己的附件。
王强查到了每件物品的价格（都是 10 元的整数倍），而他只有 N 元的预算。除此之外，他给每件物品规定了一个重要度，用整数 1 ~ 5 表示。他希望在花费不超过 N 元的前提下，使自己的满意度达到最大。
满意度是指所购买的每件物品的价格与重要度的乘积的总和，请你帮助王强计算可获得的最大的满意度。

题目链接

输入描述：
输入描述：

• 输入的第 1 行，为两个正整数N，m，用一个空格隔开。(其中 N ( N<32000 )表示总钱数， m (m <60 )为可购买的物品的个数。)
• 从第 2 行到第 m+1 行，第 j 行给出了编号为 j-1 的物品的基本数据，每行有 3 个非负整数 v 、p、 q。(其中 v 表示该物品的价格( v<10000 )， p 表示该物品的重要度( 1 ~ 5 )， q 表示该物品是主件还是附件。如果 q=0 ，表示该物品为主件，如果 q>0 ，表示该物品为附件， q 是所属主件的编号)

输出描述：
输出一个正整数，为张强可以获得的最大的满意度。

示例：

输入： 50 5
	  20 3 5
	  20 3 5
	  10 3 0
	  10 2 0
	  10 1 0
输出： 130
说明：
由第1行可知总钱数N为50以及希望购买的物品个数m为5；
第2和第3行的q为5，说明它们都是编号为5的物品的附件；
第4~6行的q都为0，说明它们都是主件，它们的编号依次为3~5；
所以物品的价格与重要度乘积的总和的最大值为10*1+20*3+20*3=130       

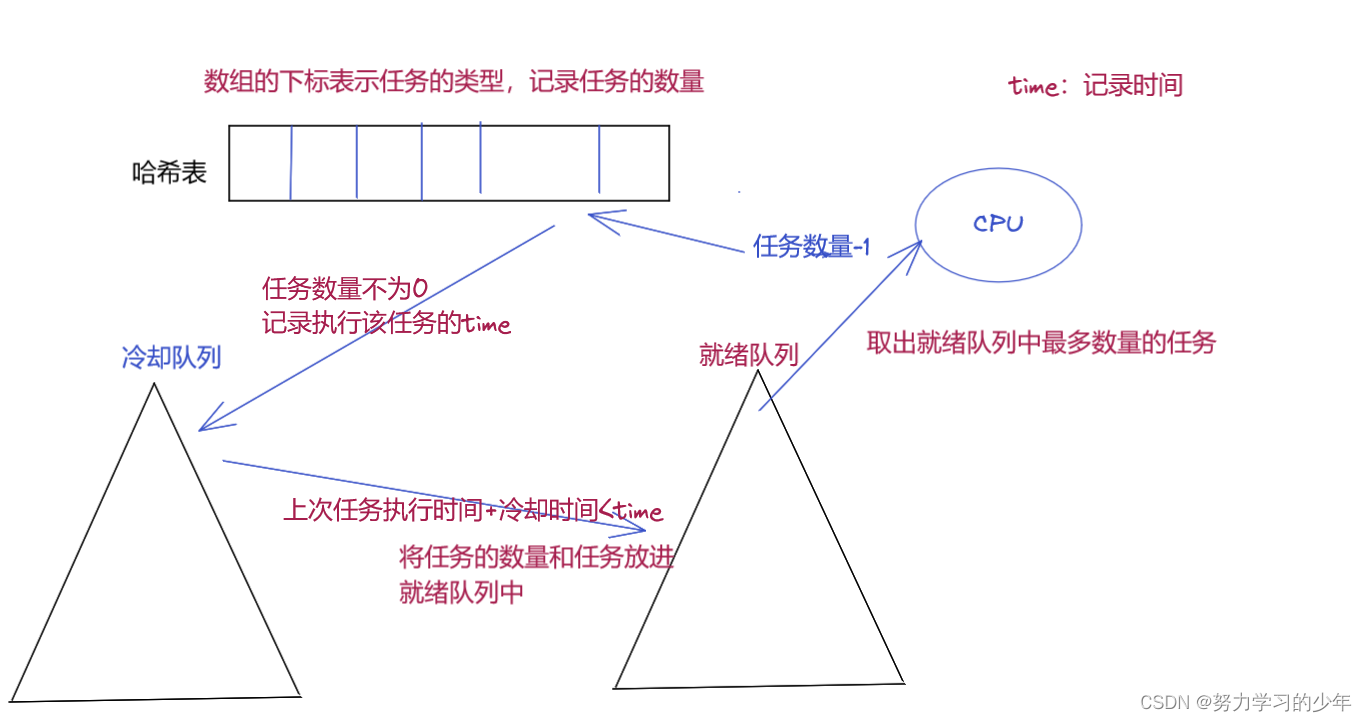
解题思路

不了解0-1背包问题的，一定先看过这篇!

本质上还是0-1背包问题，只不过多了主件和附件。假设先不看附件，那么就和0-1背包完全一样了。

对应于背包问题，主件的个数就是物品的个数，考虑每个主件时要考虑可能出现的情况，1、主件，2、主件+附件1，3、主件+附件2，4、主件+附件1+附件2，不一定每种情况都出现，只有当存在附件时才会出现对应的情况。

自定义数据存储格式，只考虑主件，其次考虑主件状态。至此，就将购物车转化为0-1背包问题了。

详细解释看下方代码注释！

代码实现

#include<iostream>
#include<math.h>
#include<bits/stdc++.h>
using namespace std;

//0-1背包问题
int shopping(vector<int>& prices, vector<int>& weights, vector<int>& index, int N){
    
	//构建附件清单：主件原数组下标 -- [<附件1的价格，附件2的重要度>， <附件1的价格，附件2的重要度>]
    unordered_map<int, vector<pair<int, int>>> umap;
    for(int i = 0; i < prices.size(); i++){
    
        if(index[i] != -1){
    
            umap[index[i]].push_back(make_pair(prices[i], weights[i]));
        }
    }
    /* 自定义数据存储格式，方便dp循环遍历时的操作，“”标记可能存在值 consume[i] : [主件价格，“主件 + 附件1 的价格”，“主件 + 附件2 的价格”，“主件 + 附件1 + 附件2 的价格”] value[i] : [主件的满意度，“主件 + 附件1 的满意度”，“主件 + 附件2 的满意度”，“主件 + 附件1 + 附件2 的满意度”] */
    vector<vector<int>> consume;
    vector<vector<int>> value;
    
    for(int i = 0; i < prices.size(); i++){
    
        if(index[i] == -1){
    
            vector<int> vec(4);
            vector<int> tor(4);
            vec[0] = prices[i];
            tor[0] = weights[i] * prices[i];
            if(umap.count(i)){
    
                vec[1] = vec[0] + umap[i][0].first;
                tor[1] = tor[0] + umap[i][0].first * umap[i][0].second;
                if(umap[i].size() == 2){
    
                    vec[2] = vec[0] + umap[i][1].first;
                    vec[3] = vec[0] + umap[i][0].first + umap[i][1].first;
                    tor[2] = tor[0] + umap[i][1].first * umap[i][1].second;
                    tor[3] = tor[0] + umap[i][0].first * umap[i][0].second + umap[i][1].first * umap[i][1].second;
                }
            }
            consume.push_back(vec);
            value.push_back(tor);
        }
    }
    //创建dp数组，此处使用到了滚动数组压缩空间的技巧，二维dp[i][j]表示值“考虑” 0 - i号主件下，只有j元时，最大的满意度！！！
    vector<int> dp(N + 1);
    /* 初始化dp[]，考虑到主件搭配附件的情况，需要将dp[]分段初始化！ 因为附件可能不存在，只存在一个，或两个附件，需要分情况考虑 按照搭配后的价格划分背包！！！ */
    if(consume[0][2]){
    
        for(int i = consume[0][0]; i < min(consume[0][1], consume[0][2]) && i <= N; i++){
    
            dp[i] = value[0][0];
        }
        
        for(int i = min(consume[0][1], consume[0][2]); i < max(consume[0][1], consume[0][2]) && i <= N; i++){
    
            if(consume[0][1] < consume[0][2]){
    
                dp[i] = value[0][1];
            }else if(consume[0][1] > consume[0][2]){
    
                dp[i] = value[0][2];
            }else{
    
                dp[i] = max(value[0][1], value[0][2]);
            }
        }
        for(int i = max(consume[0][1], consume[0][2]); i < consume[0][3] && i <= N; i++){
    
            dp[i] = max(value[0][1], value[0][2]);
        }

        for(int i = consume[0][3]; i <= N; i++){
    
            dp[i] = value[0][3];
        }
    }else if(consume[0][1]){
    
        for(int i = consume[0][0]; i < consume[0][1] && i <= N; i++){
    
            dp[i] = value[0][0];
        }
        for(int i = consume[0][1]; i <= N; i++){
    
            dp[i] = value[0][1];
        }
    }else{
    
        for(int i = consume[0][0]; i <= N; i++){
    
            dp[i] = value[0][0];
        }
    }
    
    //遍历dp[]数组，因为滚动数组压缩后，先遍历物品，在遍历背包，且背包倒序遍历！！！
    for(int i = 1; i < consume.size(); i++){
    
        for(int j = N; j >= consume[i][0]; j--){
    
            for(int k = 0; k < 4; k++){
    
            	//状态转移方程
                if(j >= consume[i][k]) dp[j] = max(dp[j], dp[j - consume[i][k]] + value[i][k]);
                else break;
            }
        }
    }
    return dp[N] * 10;
}

//主函数，程序入口
int main(){
    
    int N, n, temp;
    cin>>N>>n;
    //用来接收价格
    vector<int> prices;
    //重要度
    vector<int> weights;
    //所属主件id，需要减一
    vector<int> index;
    while(n--){
    
        cin>>temp;
        prices.push_back(temp);
        cin>>temp;
        weights.push_back(temp);
        cin>>temp;
        index.push_back(temp - 1);//减一，第一行如数组后下标为0！！！
    }
    cout<<shopping(prices, weights, index, N);
}