当前位置:网站首页>二叉树遍历
二叉树遍历
2022-07-27 09:14:00 【wfsm】
二叉树 binary tree : 每个节点最多有 2 个孩子节点
名词:
根的节点
根的子树
叶子节点 : 没有“孩子” 的 leaf
父节点 parent
兄弟节点: sibling
孩子节点: child
树的高度
左孩子 left child
右孩子 right child
满二叉树 : 一个二叉树的所有非叶子节点都存在左右孩子,并且所有的叶子节点都在同一个层级上。。。每一个分支都是满的
完全二叉树:对一个有 n 个节点的二叉树,按层级顺序编号,所有的编号从1 到 n ,,如果这个树的所有节点和同样深度的满二叉树的编号 从1到n 节点位置相同,则是完全二叉树二叉查找树 binary search tree: 对于一个节点分布均衡的二叉查找树,如果节点总数是n,那么时间复杂度为O(logn),和树的深度一样
二叉查找树,又称二叉排序树 binary sort tree
二叉堆: 一种特殊的完全二叉树,用数组存储,只要求父节点比它的左右孩子都大
二叉树自平衡: 红黑树,AVL树,数堆
二叉树遍历
在计算机程序中,遍历本身是一个线性操作,所以遍历同样具有线性结构的数组或链表,是件轻而易举的事
二叉树: 典型的非线性数据结构,遍历时需要将非线性关联节点转化成一个线性的序列
- 深度优先遍历 : 纵深,一头扎到底
- 前序
根节点在最前面,从左到右 - 中序
- 后序
- 前序
- 广度优先遍历
- 层序遍历 :二叉树按照从根节点到叶子节点的层次关系,一层一层横向遍历各个节点
绝大多数可以用递归解决的问题,其实都可以用栈 解决
因为:递归和栈都有回溯的特性
代码:
递归遍历:
public class BinaryTreeDemo {
private static class TreeNode{
int data;
TreeNode leftChild;
TreeNode rightChild;
public TreeNode(int data) {
this.data = data;
}
}
// 创建binary tree
public static TreeNode createBinaryTree(LinkedList<Integer> inputList){
TreeNode node = null;
if (inputList == null || inputList.isEmpty()){
return null;
}
Integer data = inputList.removeFirst();
if (data != null){
node = new TreeNode(data);
node.leftChild = createBinaryTree(inputList);
node.rightChild = createBinaryTree(inputList);
}
return node;
}
// 前序
public static void preOrderTraveral(TreeNode node){
if (node == null){
return;
}
System.out.println(node.data);
preOrderTraveral(node.leftChild);
preOrderTraveral(node.rightChild);
}
// 中序
public static void inOrderTraveral(TreeNode node){
if (node == null){
return;
}
inOrderTraveral(node.leftChild);
System.out.println(node.data);
inOrderTraveral(node.rightChild);
}
// 后序
public static void postOrderTraveral(TreeNode node){
if (node == null){
return;
}
postOrderTraveral(node.leftChild);
postOrderTraveral(node.rightChild);
System.out.println(node.data);
}
public static void main(String[] args) {
LinkedList<Integer> inputList = new LinkedList<>(Arrays.asList(3,2,9,null,null,10,null,null,8,null,4));
TreeNode node = createBinaryTree(inputList);
System.out.println("前序遍历");
preOrderTraveral(node);
System.out.println("中序遍历");
inOrderTraveral(node);
System.out.println("后序遍历");
postOrderTraveral(node);
}
}
栈遍历:
public class BinaryTreeStack {
private static class TreeNode{
int data;
TreeNode leftChild;
TreeNode rightChild;
public TreeNode(int data) {
this.data = data;
}
}
// 先序
public static void preOrderTraveralWithStack(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
TreeNode treeNode = root;
while (treeNode != null || !stack.isEmpty()){
while (treeNode != null){
System.out.println(treeNode.data);
stack.push(treeNode);
treeNode = treeNode.leftChild;
}
if (!stack.isEmpty()){
treeNode = stack.pop();
treeNode = treeNode.rightChild;
}
}
}
// 中序
public static void inOrderTraveralWithStack(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
TreeNode treeNode = root;
while (treeNode != null || !stack.isEmpty()){
if (treeNode != null){
stack.push(treeNode);
treeNode = treeNode.leftChild;
}else{
treeNode = stack.pop();
System.out.println("----"+treeNode.data);
treeNode = treeNode.rightChild;
}
}
}
/** * 后序遍历 : 顺序 左--右--根 * 先序遍历 : 顺序 根--左--右 * 这里我们可以想到,将先序遍历微调为: 根 -- 右 -- 左。。 然后将这些节点 出栈 ,,push到一个反向栈中,调换顺序 * 这个微调很简单,只是在push节点到栈时,先push左节点,再push右节点,,此时栈顶是右节点,,,先弹出的是右节点,再push * 到反向栈stackReverse中,再push节点 * 核心: 我们只需要增加一个栈来反向输出微调之后的先序遍历的每个节点,就可以得到后序遍历 */
public static void postOrderBinaryTreeWithStack(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
TreeNode treeNode = root;
Stack<TreeNode> stackReverse = new Stack<>();
ArrayList<Integer> list = new ArrayList<>();
stack.push(root);
while (!stack.isEmpty()){
treeNode = stack.pop();
stackReverse.push(treeNode);
// stack中右边先取出来,,stackReverse中右边先放进去,后取出来
if (treeNode.leftChild != null){
stack.push(treeNode.leftChild);
}
if (treeNode.rightChild != null){
stack.push(treeNode.rightChild);
}
}
while (!stackReverse.isEmpty()){
treeNode = stackReverse.pop();
list.add(treeNode.data);
}
System.out.println(list);
}
// 创建binary tree
public static TreeNode createBinaryTree(LinkedList<Integer> inputList){
TreeNode node = null;
if (inputList == null || inputList.isEmpty()){
return null;
}
Integer data = inputList.removeFirst();
if (data != null){
node = new TreeNode(data);
node.leftChild = createBinaryTree(inputList);
node.rightChild = createBinaryTree(inputList);
}
return node;
}
// 层序遍历
public static void levelOrderTraversalWithQueue(TreeNode root){
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode node = queue.poll();
System.out.println(node.data);
if (node.leftChild != null){
queue.offer(node.leftChild);
}
if (node.rightChild != null){
queue.offer(node.rightChild);
}
}
}
// 一个层级 :一个集合
static ArrayList<List<Integer>> levels = new ArrayList<>();
// 层序遍历-递归
public static void levelOrderTraversal(TreeNode node,int level){
if (levels.size() == level) {
// start the current level
levels.add(new ArrayList<Integer>());
}
// 填充数据
levels.get(level).add(node.data);
if (node.leftChild != null){
levelOrderTraversal(node.leftChild,level+1);
}
if (node.rightChild != null){
levelOrderTraversal(node.rightChild,level+1);
}
System.out.println("levels = " + levels);
}
public static void levelOrderTraversal(TreeNode root){
if (root == null){
return;
}
levelOrderTraversal(root,0);
}
public static void main(String[] args) {
LinkedList<Integer> inputList = new LinkedList<>(Arrays.asList(3,2,9,null,null,10,null,null,8,null,4));
TreeNode node = createBinaryTree(inputList);
System.out.println("前序遍历");
preOrderTraveralWithStack(node);
System.out.println("中序");
inOrderTraveralWithStack(node);
System.out.println("后序");
postOrderBinaryTreeWithStack(node);
System.out.println("层序遍历");
levelOrderTraversalWithQueue(node);
System.out.println("层序遍历--2");
levelOrderTraversal(node);
}
}
后序遍历: 使用一个反向栈
层序遍历: 使用队列,将子节点offer()进去就出队
边栏推荐
- 坚果天气
- npm和yarn 更新依赖包
- Install Oracle under Linux, connect local pl/sql to Oracle import table under Linux, and create new user and password
- Explanation of binary tree
- 一些实用、常用、效率越来越高的 Kubernetes 别名
- ES6 new - deconstruction assignment of array / object
- Explanation of common basic controls for C # form application (suitable for Mengxin)
- qt中使用sqlite同时打开多个数据库文件
- A survey of robust lidar based 3D object detection methods for autonomous driving paper notes
- Detailed explanation of two methods of Sqlalchemy
猜你喜欢
Restful
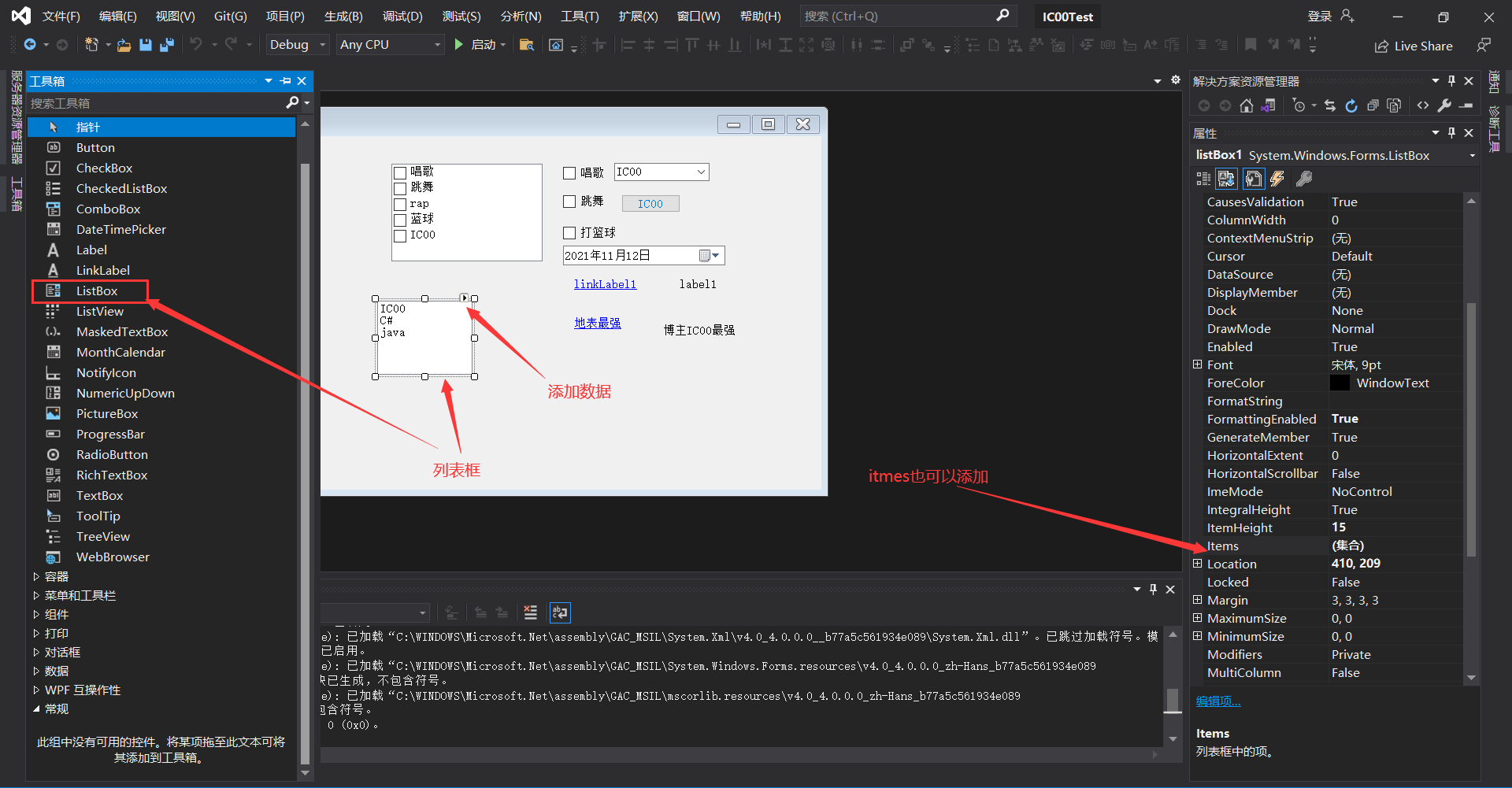
C# 窗体应用常用基础控件讲解(适合萌新)

ES6 new - Operator extension

Data interaction based on restful pages
js call和apply
![Software testing function testing a full set of common interview questions [function testing - zero foundation] essential 4-1](/img/1c/c1c1b15e502ee901a396840c01e84d.png)
Software testing function testing a full set of common interview questions [function testing - zero foundation] essential 4-1

NPM install error forced installation

Solve the problem of Chinese garbled code on the jupyter console
Wechat applet 5 - foundation strengthening (not finished)

PyTorch自定义CUDA算子教程与运行时间分析
随机推荐
500报错
pollFirst(),pollLast(),peekFirst(),peekLast()
NPM install error forced installation
Cross domain and processing cross domain
The lifecycle of arkui development framework components
基于ArkUI eTS开发的坚果食谱(NutRecipes
Solve the problem of Chinese garbled code on the jupyter console
罗克韦尔AB PLC 通过RSLinx Classic与PLC建立通信的具体方法步骤
[daily algorithm day 96] Tencent interview question: merge two ordered arrays
flex:1的原理
存储和计算引擎
ArkUI框架中的两个小技巧
一些实用、常用、效率越来越高的 Kubernetes 别名
async/await的执行顺序以及宏任务和微任务
[leetcode -- the second day of introduction to programming ability] operator (the number of bit 1 / the difference between the sum of the products of integers)
MySQL transaction
SQL exercise set
openharmony萌新贡献指南
ES6 new - string part
CUDA Programming -03: thread level