当前位置:网站首页>169. 多数元素
169. 多数元素
2022-06-26 03:20:00 【Mr Gao】
169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
思路
如果我们把众数记为 +1+1+1,把其他数记为 −1-1−1,将它们全部加起来,显然和大于 0,从结果本身我们可以看出众数比其他数多。
算法
Boyer-Moore 算法的本质和方法四中的分治十分类似。我们首先给出 Boyer-Moore 算法的详细步骤:
我们维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,count 为 0;
我们遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,我们先将 x 的值赋予 candidate,随后我们判断 x:
如果 x 与 candidate 相等,那么计数器 count 的值增加 1;
如果 x 与 candidate 不等,那么计数器 count 的值减少 1。
在遍历完成后,candidate 即为整个数组的众数。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
这题比较简单的其实:
int majorityElement(int* nums, int numsSize){
int target=1;
int nowdata=nums[0];
int i;
for(i=1;i<numsSize;i++){
if(target==0){
nowdata=nums[i];
target++;
}
else{
if(nums[i]!=nowdata){
target--;
}
else{
target++;
}
}
}
return nowdata;
}
边栏推荐
- 进度条
- Can string be changed?
- 类图
- 数字孪生智慧水务,突破海绵城市发展困境
- WebRTC系列-网络传输之6-Connections裁剪
- Double carbon bonus + great year of infrastructure construction 𞓜 deep ploughing into the field of green intelligent equipment for water conservancy and hydropower
- Qt 中 deleteLater 使用总结
- 2022年挖财证券开户安全嘛?
- Uni app custom drop-down selection list
- Nepal graph learning Chapter 3_ Multithreading completes 6000w+ relational data migration
猜你喜欢

MySQL advanced part (IV: locking mechanism and SQL optimization)

Some mobile phones open USB debugging, and the solution to installation failure
Uni app custom selection date 2 (September 16, 2021)

Analysis of technological changes in social robots
![[reading papers] fbnetv3: joint architecture recipe search using predictor training network structure and super parameters are all trained by training parameters](/img/84/2b66b513a0a36464233708fbb4b57d.png)
[reading papers] fbnetv3: joint architecture recipe search using predictor training network structure and super parameters are all trained by training parameters

Class diagram
Partition, column, list

上传文件/文本/图片,盒子阴影

Nebula Graph学习篇3_多线程完成6000w+关系数据迁移
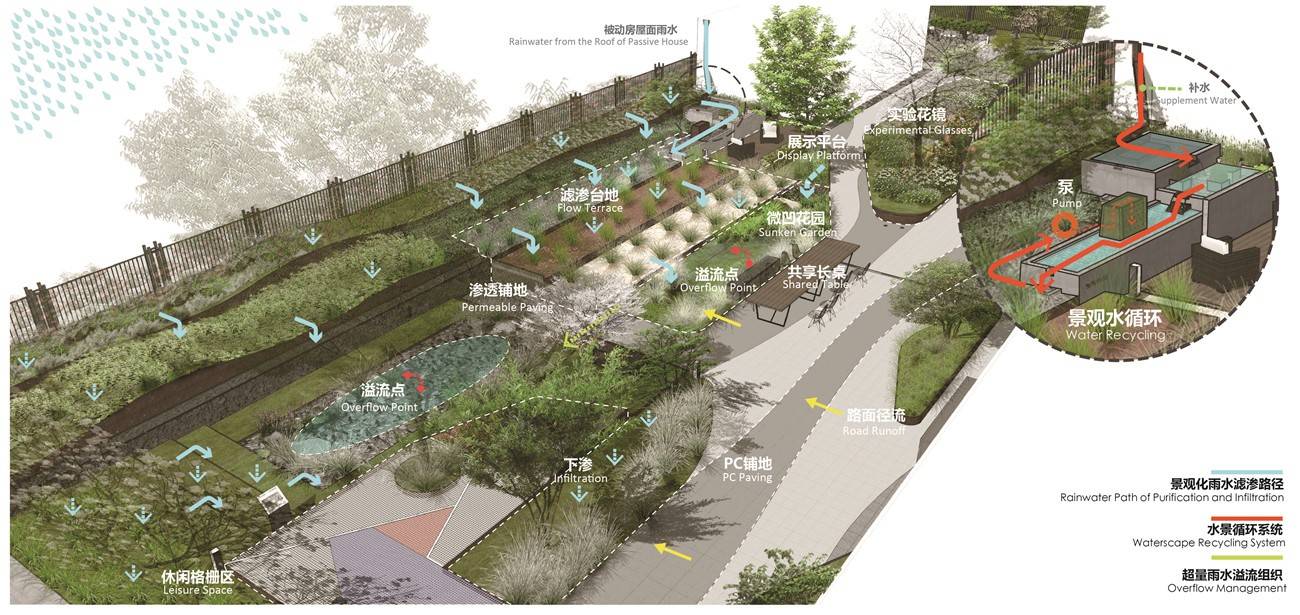
数字孪生智慧水务,突破海绵城市发展困境
随机推荐
redux-thunk 简单案例,优缺点和思考
How to prepare for a moving wedding
Gradient
MySQL addition, deletion, query and modification (Advanced)
Multimedia elements, audio, video
MySQL的视图
虚拟化是什么意思?包含哪些技术?与私有云有什么区别?
[hash table] a very simple zipper hash structure, so that the effect is too poor, there are too many conflicts, and the linked list is too long
Binary search
2022.6.25-----leetcode.剑指offer.091
Dynamic segment tree leetcode seven hundred and fifteen
[reading papers] fbnetv3: joint architecture recipe search using predictor training network structure and super parameters are all trained by training parameters
MySQL development environment
Kotlin quick start
2022.6.25-----leetcode. Sword finger offer 091
Analysis of the multiple evaluation system of children's programming
[appium stepping pit] io appium. uiautomator2. common. exceptions. InvalidArgumentException: ‘capabilities‘ are mand
面试阿里测开岗失败后,被面试官在朋友圈吐槽了......(心塞)
[hash table] improved, zipper hash structure - directly use two indexes to search, instead of hashing and% every time
Navicat16 wireless trial