当前位置:网站首页>【周赛复盘】LeetCode第81场双周赛
【周赛复盘】LeetCode第81场双周赛
2022-06-27 12:43:00 【执 梗】
目录
1、统计星号
1)题目描述
给你一个字符串
s,每 两个 连续竖线'|'为 一对 。换言之,第一个和第二个'|'为一对,第三个和第四个'|'为一对,以此类推。
请你返回不在竖线对之间,s 中'*'的数目。
注意,每个竖线'|'都会恰好属于一个对。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)先统计出所有
*的个数,然后减去两两|之前的*的个数则是答案,使用List存下所有|的下标,进行两两遍历。
4)模板代码
class Solution {
public int countAsterisks(String s) {
int n=s.length();
char[] c=s.toCharArray();
int ans=0;
List<Integer> list=new ArrayList<>();
for (int i=0;i<n;++i){
char g=c[i];
if (g=='|') list.add(i);
if (g=='*') ans++;
}
int len=list.size();
int gg=0;
for (int i = 0; i <len; i+=2) {
int l=list.get(i);
int r=list.get(i+1);
for (int j = l+1; j <r; j++) {
if (c[j]=='*') gg++;
}
}
return ans-gg;
}
}
5)算法与时间复杂度
算法:模拟
时间复杂度:遍历一次字符串,复杂度为 O ( n ) O(n) O(n)。
2、统计无向图中无法互相到达点对数
1)题目描述
给你一个整数
n,表示一张 无向图 中有n个节点,编号为0到n - 1。同时给你一个二维整数数组edges,其中edges[i] = [ai, bi]表示节点ai和bi之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)并查集的模板题,使用数组
w保存额外信息,每个连通块的点的个数,对于每个连通块,所有预期不相连的点的个数为 S S S,这有:
S = ( l o n g ) ( ( n − w [ i ] ) ∗ w [ i ] S=(long)((n-w[i])*w[i] S=(long)((n−w[i])∗w[i]
由于答案不考虑顺序,两个点只视为一种答案,所以最后答案会翻倍,我们需要把每个连通块得到的 S S S相加再除以 2 2 2。 - ( 2 ) (2) (2)我们发现,确实本质就是求一下每个连通块的大小,所以我们无论用DFS还是BFS也都非常好写。
4)模板代码
class Solution {
int N=100010;
int[] q=new int[N];
int[] w=new int[N];
public long countPairs(int n, int[][] edges) {
for (int i = 0; i < n; i++) {
q[i]=i;
w[i]=1;
}
for (int[] g:edges){
int a=g[0];
int b=g[1];
a=find(a);
b=find(b);
if (a!=b){
q[a]=b;
w[b]+=w[a];
}
}
long ans=0;
Set<Integer> set=new HashSet<>();
for (int i = 0; i < n; i++) {
int a=find(i);
if (set.contains(a)) continue;
ans+= (long)(n -w[a]) *w[a];
set.add(a);
}
return ans/2;
}
int find(int x){
if (q[x]!=x) q[x]=find(q[x]);
return q[x];
}
}
5)算法与时间复杂度
算法:并查集、BFS、DFS
时间复杂度:不进行具体分析
3、操作后的最大异或和
1)题目描述
给你一个下标从 0 开始的整数数组
nums。一次操作中,选择 任意 非负整数x和一个下标i,更新nums[i]为nums[i] AND (nums[i] XOR x)。
注意,AND 是逐位与运算,XOR 是逐位异或运算。
请你执行 任意次 更新操作,并返回nums中所有元素最大逐位异或和。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)对于位运算操作,我们可知与其二进制有关,而二进制在数据范围内不会超过
32位。二进制中位与位之间是相互独立互不影响的,为了发现规律我们去考虑每一位二进制位的情况。 - ( 2 ) (2) (2)假设我们考虑第 y y y位,由于是二进制,所以 y y y的值只可能是 0 0 0或者 1 1 1,此时我们假设 y y y为0,那么则有 0 A N D ( 0 X O R x ) 0AND(0XORx) 0AND(0XORx),因为 0 0 0与上任何值都为 0 0 0,所以无论x为多少该位都只能是 0 0 0,如果假设 y y y为 1 1 1,则有 1 A N D ( 0 X O R x ) 1AND(0XORx) 1AND(0XORx),这种情况则需要进行讨论,如果 x x x为 1 1 1,这最后结果为 1 1 1,否则为 0 0 0。
- ( 3 ) (3) (3)由此我们发现,当某个数的二进制的第 y y y位是 0 0 0时,它无法改变,当第 y y y位是 1 1 1时,它可以变成 0 0 0。对于数组内的所有数,如果存在某个数的第 y y y位为 1 1 1,那我们一定可以保证其他数的第 y y y位均是 0 0 0或者变成 0 0 0。使得所有数在异或后保证第 y y y位为 1 1 1。为了让值更大,就要保证更多的 1 1 1,我们去判断每个位是否都有 1 1 1即可,即将所有数或上即是答案。
4)模板代码
class Solution {
public int maximumXOR(int[] nums) {
int n=nums.length;
int g=nums[0];
for(int i=1;i<n;++i) g|=nums[i];
return g;
}
}
5)算法与时间复杂度
算法:位运算
时间复杂度:遍历一遍数组为 O ( n ) O(n) O(n)
4、不同骰子序列的数目
1)题目描述
给你一个整数
n。你需要掷一个 6 面的骰子n次。请你在满足以下要求的前提下,求出 不同 骰子序列的数目:
1、序列中任意 相邻 数字的 最大公约数 为1。
2、序列中 相等 的值之间,至少有2个其他值的数字。正式地,如果第i次掷骰子的值 等于 第j次的值,那么abs(i - j) > 2。
请你返回不同序列的 总数目 。由于答案可能很大,请你将答案对 1 0 9 + 7 10^9+7 109+7取余 后返回。
如果两个序列中至少有一个元素不同,那么它们被视为不同的序列。
2)原题链接
3)思路解析
- ( 1 ) (1) (1)一眼肯定是线性 d p dp dp问题,考虑到第 i i i次扔骰子被第 i − 1 i-1 i−1和 i − 2 i-2 i−2次有关,我们需要使用三维 d p dp dp存储状态方便转移。定义 f [ i ] [ k ] [ u ] f[i][k][u] f[i][k][u]为第 i i i次扔的点数为 u u u,第 i − 1 i-1 i−1次为 k k k的方案数。
- ( 2 ) (2) (2)我们可以先预处理出哪些点数是可以作为相邻的点的,对于第 i i i次丢筛子然后再去三重循环枚举 j , k , u j,k,u j,k,u,在判断符合的情况下,有转移方程:
f [ i ] [ j ] [ k ] = ( f [ i ] [ j ] [ k ] + f [ i − 1 ] [ u ] [ j ] ) f[i][j][k] = (f[i][j][k] + f[i-1][u][j]) f[i][j][k]=(f[i][j][k]+f[i−1][u][j])
4)模板代码
class Solution {
int N=10010;
int[][][] f=new int[N][7][7];
boolean[][] st=new boolean[7][7];
int mod=1000000007;
public int distinctSequences(int n) {
if (n==1) return 6;
for (int i = 1; i <=6; i++) {
for (int j = 1; j <=6; j++) {
if (i!=j&&gcd(i,j)==1){
f[2][i][j]=1;
st[i][j]=true;
}
}
}
for (int i = 3; i <=n; i++) {
for (int j = 1; j <=6; j++) {
for (int k = 1; k <=6; k++) {
if (st[j][k]&&j!=k){
for (int u = 1; u <=6; u++) {
if (st[u][j]&&k!=u&&j!=u){
f[i][j][k] = (f[i][j][k] + f[i-1][u][j]) % mod;
}
}
}
}
}
}
int res=0;
for (int i = 1; i <=6; i++) {
for (int j = 1; j <=6; j++) {
res=(res+f[n][i][j])%mod;
}
}
return res;
}
int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
}
5)算法与时间复杂度
算法:dp
时间复杂度: O ( n m 3 ) O(nm^3) O(nm3),该处 m m m为6,因为筛子只有6个面。
5、周赛总结
第三题不会位运算分析,第四题不写三维 d p dp dp,我是 s b sb sb。
边栏推荐
猜你喜欢

大小端字节序

script defer async模式

Cloud native (30) | kubernetes' app store Helm

The world's fastest download tool XDM
![[medical segmentation] unet3+](/img/93/1e9728a3dbebbf3bd9ce015552ce7a.jpg)
[medical segmentation] unet3+

Airbnb复盘微服务

On the complexity of software development and the way to improve its efficiency

Full explanation of ThreadLocal source code (threadlocalmap)
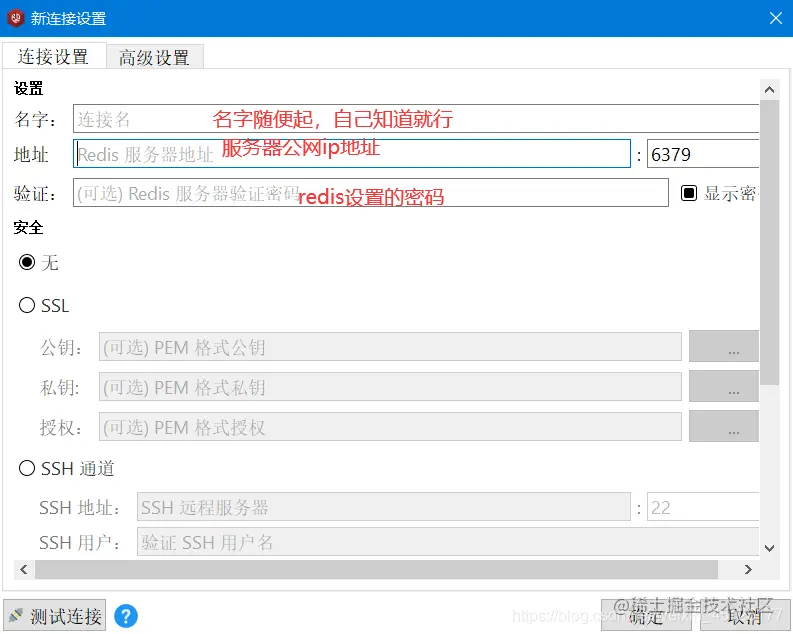
Local visualization tool connects to redis of Alibaba cloud CentOS server

Privacy computing fat offline prediction
随机推荐
【动态规划】—— 背包问题
外包2年的我终于上岸了!记录我的字节跳动3轮面试,希望帮助到大家!
Two TCP flow control problems
L June training (day 27) - figure
云原生(三十) | Kubernetes篇之应用商店-Helm
Nmcli team bridge basic configuration
Quanzhi A13 tossing memo
深信服X计划-系统基础总结
An interesting experiment of netmask
nifi从入门到实战(保姆级教程)——身份认证
Snipaste, the world's strongest screenshot software
ssh工作流程及原理
Vs debugging skills
LeetCode_ Fast power_ Recursion_ Medium_ 50.Pow(x, n)
隐私计算FATE-离线预测
Tiktok practice ~ public / private short video interchange
今日睡眠质量记录78分
Viewpager2 usage record
【TcaplusDB知识库】TcaplusDB-tcapsvrmgr工具介绍(三)
【医学分割】unet3+


