当前位置:网站首页>“蔚来杯“2022牛客暑期多校训练营2,签到题GJK
“蔚来杯“2022牛客暑期多校训练营2,签到题GJK
2022-07-29 01:25:00 【小哈里】
题号 标题 已通过代码 通过率 团队的状态
A Falfa with Polygon 点击查看 56/445
B light 点击查看 50/326
C Link with Nim Game 点击查看 192/1035
D Link with Game Glitch 点击查看 831/6211
E Falfa with Substring 点击查看 264/3287
F NIO with String Game 点击查看 52/412
G Link with Monotonic Subsequence 点击查看 1667/7564
H Take the Elevator 点击查看 290/769
I let fat tension 点击查看 204/454
J Link with Arithmetic Progression 点击查看 1407/7990
K Link with Bracket Sequence I 点击查看 996/3057
L Link with Level Editor I 点击查看 564/2616
文章目录
G.Link with Monotonic Subsequence
题意:
- 官方

思路:
- 开始想的是构造(1, 2, 3, 4)(9, 8, 7, ,6 , 5)这样的排列,这样前面一个组最多与后面的组中的一个形成LIS,答案就是n/2+1,然后再想可以多弄几个组,就可以变得更小。
- 构造形如(3, 2, 1),( 6, 5, 4),( 9, 8, 7) 的排列,这样每个组与后一个组都只能选一个,然后如果组数变多,长度也会变大,在此基础上要让每组元素相对更多,所以就是继续求平均的根号n,即每组根号n个元素即可。
- 注意要向上取整,因为比如7的时候,介于2~3之间,我们肯定是选3来让组数变得更少。
#include<bits/stdc++.h>
using namespace std;
int main(){
int T; cin>>T;
while(T--){
int n; cin>>n;
int sq = ceil(sqrt(n));
for(int i = n; i > 0; i -= sq){
//(7 8 9 )(4 5 6) (1 2 3)
for(int j = max(1,i-sq+1); j <= i; j++)
cout<<j<<" ";
}
cout<<"\n";
}
return 0;
}
J.Link with Arithmetic Progression
题意:
- 官方:

思路:
官方:

讲一下线性回归
最小二乘法,即最小化残差的平方和,就是本题要求的值,等差数列和当前数列的差值平方。
证明过程可以参考:https://zhuanlan.zhihu.com/p/73494604,
公式可以参考:https://blog.csdn.net/snowdroptulip/article/details/79020590
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double LD;
const int maxn = 1e6+10;
int a[maxn];
int main(){
int T; cin>>T;
while(T--){
LD n; cin>>n;
LD x = 0, y = 0; //坐标(i,a[i])
for(int i = 1; i <= n; i++){
cin>>a[i];
x += i; y += a[i];
}
x /= n; y /= n; //期望E(x),E(y),即x,y均值
LD s1 = 0, s2 = 0;
for(int i = 1; i <= n; i++){
s1 += (i-x)*(a[i]-y); //协方差:Cov(X,Y) = E[(X-E[X])(Y-E[Y])]?
s2 += (i-x)*(i-x); //方差:D(x) = E[(X-E[X])(X-E[X])]
}
LD k = s1/s2, b = y-k*x; //公式
LD ans = 0;
for(int i = 1; i <= n; i++){
ans += (a[i]-k*i-b)*(a[i]-k*i-b);
}
printf("%.15Lf\n",ans);
}
return 0;
}
- 三分做法
已知f(x)在l,r上单峰且连续,求极值。每次迭代将当前区间的长度缩小1/3直到找到极值。
前面我们知道等差数列是一条直线,这条直线与所有给出的点(i,a[i])求方差最小时就是要找的点。
所以设直线y = kx+b ,即b^2=(y-kx)^2,令y=a[i], x=i,此时我们只需要最小化b的方差即可。
b关于k单峰且连续,b=f(k)。
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
typedef long double LD;
const LL maxn = 1e6+10;
const LD eps = 1e-10;
LD a[maxn], b[maxn], n;
LD check(LD k){
//b=y-kx的方差
LD sum = 0, res = 0;
for(int i = 1; i <= n; i++){
b[i] = a[i]-k*i;
sum += b[i];
}
sum /= n;
for(int i = 1; i <= n; i++){
res += (b[i]-sum)*(b[i]-sum);
}
return res;
}
int main(){
IOS;
int T; cin>>T;
while(T--){
cin>>n;
LD sum = 0;
for(int i = 1; i <= n; i++){
cin>>a[i]; sum += a[i];
}
LD l = -1e15, r = 1e15, ans = 1e100;
while(r-l > eps){
LD mt = (r-l)/3;
LD m1 = l+mt, m2 = r-mt;
LD v1 = check(m1), v2 = check(m2);
if(v1 >= v2){
ans = min(ans, v2);
l = m1;
}else{
ans = min(ans, v1);
r = m2;
}
}
printf("%.15Lf\n",ans);
}
return 0;
}
K.Link with Bracket Sequence I
题意:
- 官方:

思路:
- 官方

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
const int maxn = 210;
const int mod = 1e9+7;
LL f[maxn][maxn][maxn];//b前i位,'('比')'多j个,a前k位的方案数
int main(){
IOS;
int T; cin>>T;
while(T--){
int n, m; cin>>n>>m;
string a; cin>>a;
a = "0"+a;
// memset(f,0,sizeof(f)); //TLE 70%
for (int i = 0; i <= m; ++ i) {
for (int j = 0; j <= m; ++ j) {
for (int k = 0; k <= m; ++ k) {
f[i][j][k] = 0;
}
}
}
f[0][0][0] = 1;
for(int i = 0; i < m; i++){
for(int j = 0; j <= i; j++){
for(int k = 0; k <= i; k++){
//对于b[i+1], a[k+1]选或不选
if(a[k+1]==')'){
if(j>0)(f[i+1][j-1][k+1] += f[i][j][k]) %= mod;
(f[i+1][j+1][k] += f[i][j][k]) %= mod;
}else if(a[k+1]=='('){
(f[i+1][j+1][k+1] += f[i][j][k]) %= mod;
if(j>0)(f[i+1][j-1][k] += f[i][j][k]) %= mod;
}else {
(f[i+1][j+1][k] += f[i][j][k]) %= mod;
if(j>0)(f[i+1][j-1][k] += f[i][j][k]) %= mod;
}
}
}
}
cout<<f[m][0][n]<<"\n";
}
return 0;
}
边栏推荐
- The growth path of embedded engineers
- What is browser fingerprint recognition
- JS dom2 and dom3
- QT memory management tips
- Large scale web crawling of e-commerce websites (Ultimate Guide)
- Understand the working principle of timer in STM32 in simple terms
- The solution of reducing the sharpness of pictures after inserting into word documents
- leetcode/和大于等于target的连续最短子数组
- druid. io kill -9 index_ Realtime traceability task
- Leetcode 242. valid anagram
猜你喜欢

数学建模——带相变材料的低温防护服御寒仿真模拟
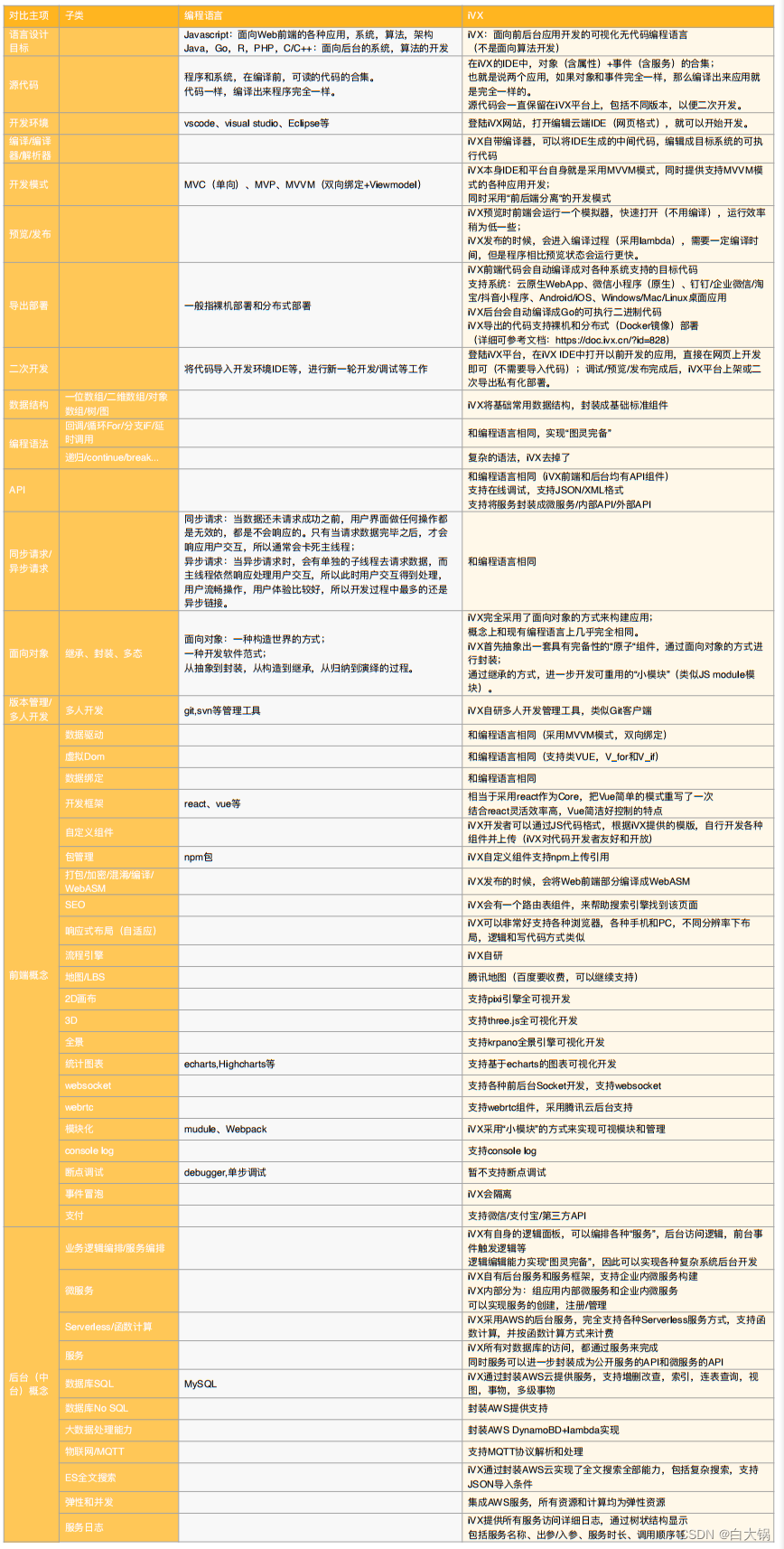
iVX低代码平台系列详解 -- 概述篇(二)
![[golang] use select {}](/img/30/fa593ec682a40c47689c1fd88f9b83.png)
[golang] use select {}

Wonderful use of data analysis

Lm13 morphological quantification momentum period analysis

Web crawler API Quick Start Guide

Lxml web page capture the most complete strategy

Implementation of 10m multifunctional signal generator with FPGA

数学建模——自来水管道铺设问题

Nine days later, we are together to focus on the new development of audio and video and mystery technology
随机推荐
Control the pop-up window and no pop-up window of the input box
As long as I run fast enough, it won't catch me. How does a high school student achieve a 70% salary increase under the epidemic?
Mathematical modeling -- Optimization of picking in warehouse
数学建模——带相变材料的低温防护服御寒仿真模拟
What is a proxy server? [2022 guide]
Anti crawler mechanism solution: JS code generates random strings locally
Ciscn 2022 central China Misc
Thirty years of MPEG audio coding
Mathematical modeling -- cold proof simulation of low temperature protective clothing with phase change materials
Dynamic memory and smart pointer
Process -- user address space and kernel address space
【流放之路-第二章】
[golang] use select {}
[public class preview]: application exploration of Kwai gpu/fpga/asic heterogeneous platform
DSP vibration seat
【云原生与5G】微服务加持5G核心网
12.< tag-动态规划和子序列, 子数组>lt.72. 编辑距离
Lua third-party byte stream serialization and deserialization module --lpack
Force deduction brush question (2): sum of three numbers
为什么 BI 软件都搞不定关联分析