当前位置：网站首页>深度学习基础-基于Numpy的循环神经网络（RNN）实现和反向传播训练

深度学习基础-基于Numpy的循环神经网络（RNN）实现和反向传播训练

2022-08-01 23:15:00 【LeonYi】

本文是深度学习入门：基于Python的实现、神经网络与深度学习（NNDL）以及动手学深度学习的读书笔记。本文将介绍基于Numpy的循环神经网络的前向传播和反向传播实现，包括RNN、LSTM和GRU。

一、概述

1.1 循环神经网络（RNN）

循环神经网络（Recurrent Neural Networks, RNN）是一类具有短期记忆能力的神经网络，其特点是在处理序列数据时，能够记录历史信息。RNN已经被广泛应用序列数据上，例如语言模型、语音识别、自然语言生成、机器翻译以及时间序列等任务上。 RNN可以被理解为一种迭代地利用当前时刻信息及历史信息来更新短期记忆的网络。通过数据的循环，RNN能一边记住历史的信息，一边更新到最新的信息。RNN通常按时间展开其计算图以便于理解其计算过程，具体如上图所示。在后文中，本文用RNN代指简单的循环神经网络。

理论上，一个完全连接的循环网络是任何非线性动力系统的近似器。RNN可以处理任意长的序列。但是在实际中，简单的RNN通常会面临梯度消失和梯度爆炸问题，使其不能建模好序列的长期依赖。

具体地，RNN是一个非常简单的循环神经网络，它是只有一个隐藏层的神经网络。RNN在时刻$t$的更新公式如下所示：\[ \mathbf{h}_t = \tanh \left( \mathbf{h}_{t-1}\mathbf{W}_{\text{h}} + \mathbf{x}_t \mathbf{W}_{\text{x}} + \mathbf{b} \right)\] 其中，向量$\mathbf{h}_t \in \mathbb{R}^{1 \times d}$为RNN的隐藏状态，而$\mathbf{x}_t \in \mathbb{R}^{1 \times m}$是网络在时刻$t$的输入，则$\mathbf{h}_t $不仅和当前时刻的输入$\mathbf{x}_t$相关，也和上一个时刻的隐藏状态$\mathbf{h}_{t-1}$相关。此外，$\mathbf{W}_{\text{h}} \in \mathbb{R}^{d \times d}$和$\mathbf{W}_{\text{x}} \in \mathbb{R}^{m \times d}$分别表示状态-状态权重矩阵和状态-输入权重矩阵。

在这里，RNN可被进一步表示为$\mathbf{h}_t = \tanh \left( \mathbf{z}_{t} \right)$，其中$\mathbf{z}_t$为RNN在时刻$t$的净输入,有$\mathbf{z}_t = \mathbf{h}_{t-1}\mathbf{W}_{\text{h}} + \mathbf{x}_t \mathbf{W}_{\text{x}} +\mathbf{b} $。注意，本文为了便于编程实现，将向量均表示为行向量。

1.2 RNN的应用

RNN可以应用到很多不同类型的机器学习任务。根据这些任务的特点，其主要可被分为: 序列到类别模式、序列到序列模式。

1.2.1 序列到类别

序列到类别模式主要用于输入为序列、输出为类别的序列数据的分类问题，例如时间序列分类、文本分类。比如在文本分类中，输入数据为单词序列，输出为该文本的类别。

假设一个实例$\mathbf{X} =[\mathbf{x}_{1} , \mathbf{x}_{2}, \ldots,\mathbf{x}_{T}] \in \mathbb{R}^{T \times m}$为一个长度为$T$的序列，输出为一个类别$\mathcal{Y} = \{1, \ldots, C\}$。可将实例$\mathbf{X}$按不同时刻输入到RNN中，并得到不同时刻的隐藏状态$\mathbf{h}_{1} , \mathbf{h}_{2}, \ldots,\mathbf{h}_{T}$。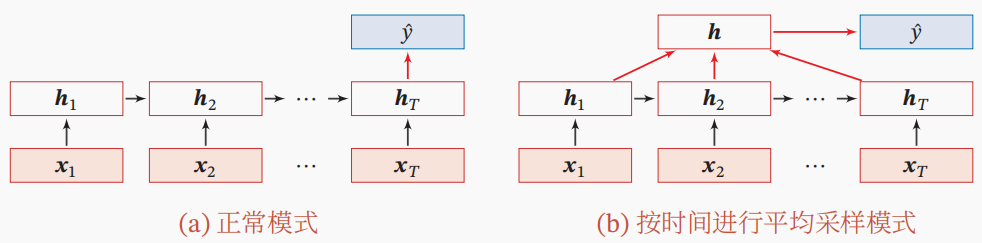

这时，可选择将最后时刻的状态$\mathbf{h}_{T}$作为整个序列的表示，也可对所有的隐藏状态进行汇聚，把这个汇聚后的状态$\mathbf{s} \in \mathbb{R}^{1 \times d}$作为整个序列的最终表示。其操作如上图所示。具体地，有:\[ \mathbf{s} = \operatorname{Pooling} \big( \mathbf{h}_{1} , \mathbf{h}_{2}, \ldots,\mathbf{h}_{T}\big) \]其中，汇聚操作可使用平均或注意力机制。然后，我们可将序列的最终表示$\mathbf{s}$送入简单的线性层或多层前馈神经网络（Feed Forward Network,FFN）用于分类。

当然，也可将其用于回归任务中。此外，这一架构稍加改造，便可以用于语言模型或者序列化推荐中（通常是自回归的形式，即基于历史的序列，预测序列的下一个时刻未知的元素）

1.2.2 序列到序列

序列到序列（Sequence-to-Sequence）可分为同步的序列到序列和异步的序列到序列。

同步的序列到序列模式主要用于序列标注（Sequence Labeling）任务，即每一时刻都有输入和输出，输入序列和输出序列的长度相同。其具体应用有，视频分类、词性标注等。比如，在词性标注（Part-of-Speech Tagging）中，每一个单词都需要标注其对应的词性标签。 异步的序列到序列模式也称为编码器-解码器（Encoder-Decoder）模型，即输入序列和输出序列不需要有严格的对应关系，也不需要保持相同的长度。其具体应用有，文本摘要、图像理解（Image Caption）、问答系统（Question Answering system）、机器翻译等。比如在机器翻译中，输入为源语言的单词序列，输出为目标语言的单词序列。

1.3 模型学习

RNN的参数可以通过梯度下降方法，例如SGD，来进行学习。以同步的序列到序列模式为例，给定一个训练样本$(\mathbf{X}, \mathbf{y})$，其中$\mathbf{y} \in \mathbb{R}^{1 \times T}$是长度为$T$的标签序列。

RNN的参数关于某一时间步$t$的损失$L_t$（交叉熵损失），那么整个序列的损失函数为$L=\sum_{i=1}^{T} L_t$ 。整个序列的损失函数$L$关于参数的梯度为：\[ \frac{\partial L} {\partial \mathbf{W}_h}=\sum_{t=1}^{T} \frac{\partial L_t} {\partial \mathbf{W}_h} \] 即每个时刻损失$L_t$对参数$\mathbf{W}_h$的偏导数之和。由于，RNN存在循环的计算过程，其计算梯度的方式和FFN不同。通常，需展开其计算图，然后按时间来进行梯度反向传播（Backpropagation Through Time，BPTT）。

1.3.1 按时间反向传播BPTT

BPTT算法将RNN看作一个展开的多层FFN，其中“每一层”对应RNN中的每个时间步，此时RNN可视为在水平方向上延伸的神经网络（相当于T层参数共享的FFN），它可按FFN中的反向传播算法计算参数的梯度。

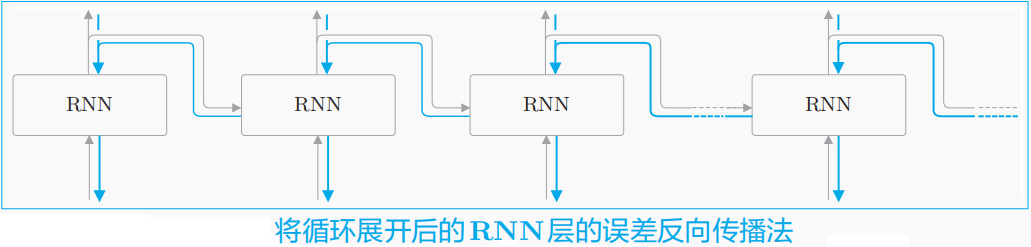
如上图所示，将循环展开后的RNN可使用反向传播。换句话说，可通过先进行正向传播，再进行反向传播的方式求目标梯度（直观地，只需要从损失开始，将其梯度不断反向传播回去，已求解各个参数的梯度）。在“展开”的RNN中所有层的参数是共享的，因此参数的真实梯度是所有展开层（时间步）的参数的梯度之和。

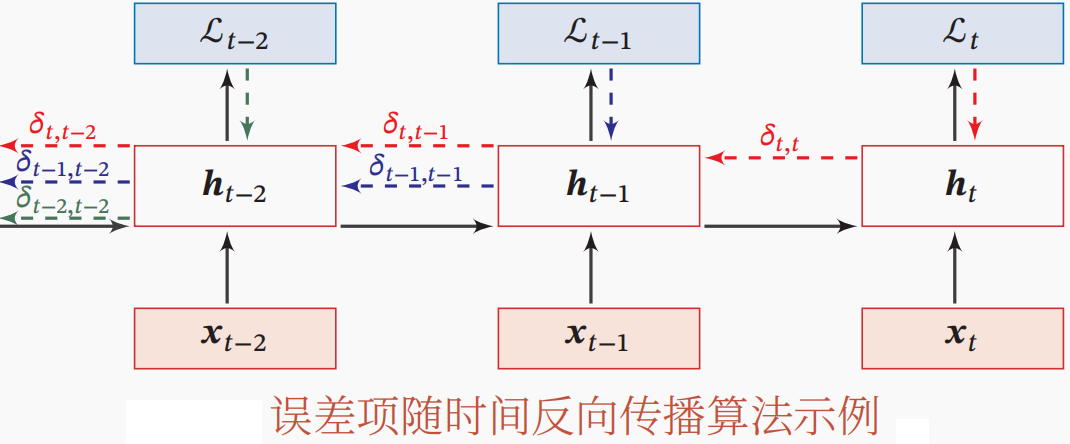
以时间步t时的损失为例，参数将是各个时间步t时的损失之和。具体地，考虑时间步t时的损失，参数的梯度是参数在所有的时间步的梯度之和。

1.3.1 截断BPTT

尽管通过BPTT，RNN的学习似乎可以进行，但在这之前还有一个须解决的问题，那就是学习长时序数据的问题。因为随着时序数据的时间跨度的增大，BPTT 消耗的计算机资源也会成比例地增大。另外，反向传播的梯度也会变得不稳定。

二、RNN实现

2.1 简单RNN

这里以RNN用于语言模型为例，试图建模马尔科夫链对应的条件概率分布。

# coding: utf-8
import numpy as np


class TimeEmbedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.layers = None
        self.W = W

    def forward(self, xs):
        N, T = xs.shape
        V, D = self.W.shape

        out = np.empty((N, T, D), dtype='f')
        self.layers = []

        for t in range(T):
            layer = Embedding(self.W)
            out[:, t, :] = layer.forward(xs[:, t])
            self.layers.append(layer)

        return out

    def backward(self, dout):
        N, T, D = dout.shape

        grad = 0
        for t in range(T):
            layer = self.layers[t]
            layer.backward(dout[:, t, :])
            grad += layer.grads[0]

        self.grads[0][...] = grad
        return None


 class TimeRNN:
    def __init__(self, Wx, Wh, b, stateful=False):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.layers = None

        self.h, self.dh = None, None
        self.stateful = stateful

    def forward(self, xs):
        Wx, Wh, b = self.params
        N, T, D = xs.shape
        D, H = Wx.shape

        self.layers = []
        hs = np.empty((N, T, H), dtype='f')

        if not self.stateful or self.h is None:
            self.h = np.zeros((N, H), dtype='f')

        for t in range(T):
            layer = RNN(*self.params)
            self.h = layer.forward(xs[:, t, :], self.h)
            hs[:, t, :] = self.h
            self.layers.append(layer)

        return hs

    def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D, H = Wx.shape

        dxs = np.empty((N, T, D), dtype='f')
        dh = 0
        grads = [0, 0, 0]
        for t in reversed(range(T)):
            layer = self.layers[t]
            dx, dh = layer.backward(dhs[:, t, :] + dh)
            dxs[:, t, :] = dx

            for i, grad in enumerate(layer.grads):
                grads[i] += grad

        for i, grad in enumerate(grads):
            self.grads[i][...] = grad
        self.dh = dh

        return dxs

    def set_state(self, h):
        self.h = h

    def reset_state(self):
        self.h = None


 class TimeAffine:
    def __init__(self, W, b):
        self.params = [W, b]
        self.grads = [np.zeros_like(W), np.zeros_like(b)]
        self.x = None

    def forward(self, x):
        N, T, D = x.shape
        W, b = self.params

        rx = x.reshape(N*T, -1)
        out = np.dot(rx, W) + b
        self.x = x
        return out.reshape(N, T, -1)

    def backward(self, dout):
        x = self.x
        N, T, D = x.shape
        W, b = self.params

        dout = dout.reshape(N*T, -1)
        rx = x.reshape(N*T, -1)

        db = np.sum(dout, axis=0)
        dW = np.dot(rx.T, dout)
        dx = np.dot(dout, W.T)
        dx = dx.reshape(*x.shape)

        self.grads[0][...] = dW
        self.grads[1][...] = db

        return dx

       
class SimpleRnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn

        # 初始化权重
        embed_W = (rn(V, D) / 100).astype('f')
        rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
        rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
        rnn_b = np.zeros(H).astype('f')
        affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # 生成层
        self.layers = [
            TimeEmbedding(embed_W),
            TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
            TimeAffine(affine_W, affine_b)
        ]
        self.loss_layer = TimeSoftmaxWithLoss()
        self.rnn_layer = self.layers[1]

        # 将所有的权重和梯度整理到列表中
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

    def forward(self, xs, ts):
        for layer in self.layers:
            xs = layer.forward(xs)
        loss = self.loss_layer.forward(xs, ts)
        return loss

    def backward(self, dout=1):
        dout = self.loss_layer.backward(dout)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)
        return dout

    def reset_state(self):
        self.rnn_layer.reset_state()