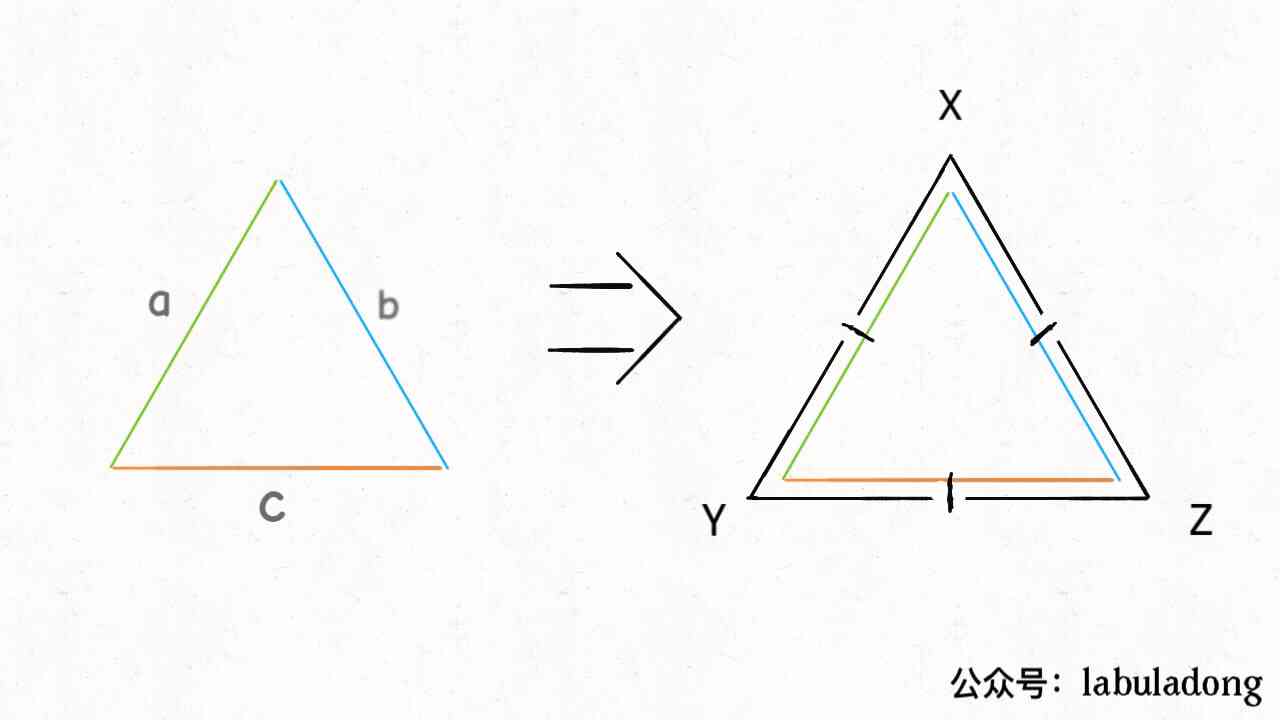作者|Samarendra Chandan Bindu Dash
编译|Flin
来源|analyticsvidhya
介绍
在本文中,我们将深入研究一种有趣的算法,称为“接缝雕刻”。调整图像的大小而不裁剪或扭曲其内容似乎是不可能完成的任务。我们将逐步构建,从头开始实现接缝雕刻算法,同时查看其背后的一些有趣的数学原理。
微积分方面的知识将有助于后续学习,但不是必需的。我们开始吧。
(本文的灵感来自麻省理工学院的格兰特·桑德森的演讲。)
问题
让我们看一下这张图片。

萨尔瓦多·达利(Salvador Dali)完成的这幅画被命名为“记忆的永恒”。我们对绘画的内容更感兴趣,而不是其艺术价值。我们要通过减小图片的宽度来调整图片的大小。我们可以想到的两个有效过程是裁剪图片或压缩宽度。

但是,正如我们所看到的,裁剪会删除许多对象,挤压又会扭曲图片。我们希望两者兼有,即在不裁剪任何对象或不扭曲对象的情况下减小宽度。
我们可以看到,除了对象之外,图片中还有很多空白。我们要在此处完成的任务是以某种方式删除对象之间的空白区域,以便保留图像中有趣的部分,同时丢弃不必要的空间。
这确实是一个棘手的问题,很容易迷失。因此,将问题分解为更小,更易于管理的部分始终是一个好主意。我们可以将这个问题分为两个部分。
-
识别图片中有趣的部分(即对象)。
-
标识可以去除而不会扭曲图片的像素路径。
识别对象
在继续之前,我们需要将图片转换为灰度图像。这将对我们稍后进行的操作很有帮助。这是一个将RGB像素转换为灰度值的简单公式

def rgbToGrey(arr):
greyVal = np.dot(arr[...,:3], [0.2989, 0.5870, 0.1140])
return np.round(greyVal).astype(np.int32)

为了识别对象,我们可以制定策略。如果我们能以某种方式识别图片中的所有边缘呢?然后,我们可以要求接缝雕刻算法采用不通过边缘的像素路径,因此,通过扩展,不会碰触任何由边缘封闭的区域。
但是,我们如何识别边缘呢?我们可以看到的一个观察结果是,每当两个相邻像素之间的颜色发生急剧变化时,最有可能就是物体的边缘。我们可以将这种立即的颜色变化合理化,作为从该像素开始的新对象的开始。
我们必须解决的下一个问题是如何识别像素值的急剧变化。现在,让我们考虑一个简单的情况,即一行像素。假设我们将此值数组表示为x。

我们可以取像素x [i + 1],x [i]之间的差。它会显示当前像素从右侧变化了多少。或者我们也可以取x [i]和x [i-1]之差,这将在左侧产生变化。为了表示总变化,我们可能要取两者的平均值,得出

熟悉微积分的任何人都可以快速地将此表达式识别为导数的定义。我们需要计算x值的急剧变化,因此我们正在计算它的导数。如果我们定义一个过滤器[ -0.5,0,0.5 ],然后用数组[x[i-1],x[i],x[i+1]乘以它的元素,然后取它的和,它就会得到x[i]的导数。
由于我们的图片是2D的,因此我们需要2D过滤器。我不会详细介绍,但是我们过滤器的2D版本看起来像这样,

当我们的过滤器计算沿x轴的每个像素的导数时,它将给出垂直边缘。同样,如果我们沿y轴计算导数,则将具有水平边缘。过滤器如下。(与转置时用于x轴的过滤器相同。)

这些过滤器也称为Sobel过滤器。
所以,我们有两个过滤器,需要在图片中传播。对于每个像素,用(3X3)子矩阵对其进行逐元素乘法,然后取其和。这种运算被称为卷积。

卷积:
数学上,卷积运算就是这样,

看看我们如何对两个函数进行逐点乘法,然后对其进行积分。从数值上讲,这将与我们之前所做的相对应,即过滤器和图像的逐元素相乘,然后对其求和。
注意,对于k函数,它如何写为k(t-τ)。因为卷积运算需要翻转其中一个信号。你可以直观地将其想象成这样:两列火车在一条直线的水平轨道上相互朝着一个不可避免的碰撞(不必担心,因为它们是叠加的,火车不会发生任何事情)。因此,火车头将彼此面对。现在,假设你正在从左到右扫描轨道。然后,对于左列火车,你将从尾部向头部扫描。
同样,计算机需要从右下角(2,2)角到左上角(0,0)而不是从左上角到右下角读取过滤器。因此,实际的Sobel过滤器如下所示,

在进行卷积运算之前,我们先进行180度旋转。

我们可以继续编写一个简单的实现来进行卷积运算。像这样:
def naiveConvolve(img,ker):
res = np.zeros(img.shape)
r,c = img.shape
rK,cK = ker.shape
halfHeight,halfWidth = rK//2,cK//2
ker = np.rot90(ker,2)
img = np.pad(img,((1,1),(1,1)),mode='constant')
for i in range(1,r+1):
for j in range(1,c+1):
res[i-1,j-1] = np.sum(np.multiply(ker,img[i-halfHeight:i+halfHeight+1,j-halfWidth:j+halfWidth+1]))
return res
这将很好地工作,但是将花费大量时间来执行,因为它将进行近9 * r * c的乘法和加法运算以得出结果。但是我们可以聪明地使用数学中的更多概念来大大减少时间复杂度。
快速卷积:
卷积具有有趣的性质。时域中的卷积对应于频域上的乘法。即

,其中F(w)表示频域中的函数。
我们知道傅立叶变换将时域的信号转换成其频域。因此,我们可以做的是计算图像和滤波器的傅立叶变换,将它们相乘,然后进行傅立叶逆变换以获得卷积结果。
为此我们可以使用NumPy库。
def fastConvolve(img,ker):
imgF = np.fft.rfft2(img)
kerF = np.fft.rfft2(ker,img.shape)
return np.fft.irfft2(imgF*kerF)
(注意:在某些情况下,得出来的值可能与朴素方法稍有不同,因为fastConvolve函数会计算圆形卷积。但是实际上,我们可以轻松地使用快速卷积,而不必担心这些较小的值差异。)
酷!现在,我们有了一种有效的方法来计算水平边缘和垂直边缘,即x和y分量。因此,使用

def getEdge(greyImg):
sX = np.array([[0.25,0.5,0.25],
[0,0,0],
[-0.25,-0.5,-0.25]])
sY = np.array([[0.25,0,-0.25],
[0.5,0,-0.5],
[0.25,0,-0.25]])
#edgeH = naiveConvolve(greyImg,sX)
#edgeV = naiveConvolve(greyImg,sY)
edgeH = fastConvolve(greyImg,sX)
edgeV = fastConvolve(greyImg,sY)
return np.sqrt(np.square(edgeH) + np.square(edgeV))
识别像素路径:
对于连续路径,我们可以定义一个规则,即每个像素仅连接到它下面的3个最近的像素。这将使像素从上到下具有连续的路径。因此,我们的子问题成为基本的寻路问题,我们必须将成本降到最低。
由于边缘具有更高的幅度,如果我们继续以最低的成本移除像素路径,它将避免出现边缘。
让我们定义一个函数“ cost”,该函数获取一个像素并计算从那里到图片结尾的最小成本像素路径。我们有以下观察,
- 在最底行(即i = r-1)

- 对于任何中间像素,

代码:
def findCostArr(edgeImg):
r,c = edgeImg.shape
cost = np.zeros(edgeImg.shape)
cost[r-1,:] = edgeImg[r-1,:]
for i in range(r-2,-1,-1):
for j in range(c):
c1,c2 = max(j-1,0),min(c,j+2)
cost[i][j] = edgeImg[i][j] + cost[i+1,c1:c2].min()
return cost
绘图:
我们可以在图中看到三角形。它们表示不返回的点,也就是说,如果你到达那个像素,就没有一条路径不通过边缘到达底部。而这正是我们试图避免的。
从成本矩阵中寻找像素路径可以很容易地用贪婪算法完成。在最上面一行找到最小成本像素,然后向下移动,在所有连接到它的像素中选择成本最低的像素。
def findSeam(cost):
r,c = cost.shape
path = []
j = cost[0].argmin()
path.append(j)
for i in range(r-1):
c1,c2 = max(j-1,0),min(c,j+2)
j = max(j-1,0)+cost[i+1,c1:c2].argmin()
path.append(j)
return path
为了删除路径定义的接缝,我们只需要遍历每一行并删除路径数组提到的列。
def removeSeam(img,path):
r,c,_ = img.shape
newImg = np.zeros((r,c,3))
for i,j in enumerate(path):
newImg[i,0:j,:] = img[i,0:j,:]
newImg[i,j:c-1,:] = img[i,j+1:c,:]
return newImg[:,:-1,:].astype(np.int32)
在这里,我已经预先计算了100个接缝雕刻操作。


我们可以看到画中的物体是如何彼此接近的。我们已经成功地使用接缝切割算法缩小了图像的大小,而不会对物体造成任何变形。我已经附上了完整代码链接。感兴趣的读者可以在这里看看。
总的来说,接缝雕刻是一个有趣的算法。它有一些警告,因为如果提供的图像有太多的细节或太多的边缘,它将失败。
使用该算法对不同的图片进行修改以查看最终结果总是很有趣的。如果你有任何疑问或建议,请给我留言。
感谢你的阅读!
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/