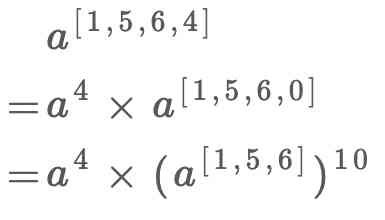题目下图所示:

题目大意是给定一个n*n的矩阵,每行从左到右和每列从上到下是递增的序列,找出矩阵中第k小的数。
方案一:
最简单的方式是将矩阵中的数都放在一个序列中,重新由小到大排序,然后输出第k个数,暴力解法。
实现代码:
class Solution { public: int kthSmallest1(vector<vector<int>>& matrix, int k) { int m[200001]; int nNum = 0; for(int i=0; i<matrix.size(); i++) { for(int j=0; j<matrix[i].size(); j++) { m[nNum++] = matrix[i][j]; } } sort(m, m+nNum); return m[k-1]; } };
方案二:
因为矩阵每行和每列都是有序的,可以使用二分查找来进行;取矩阵中前后两个数值的平均值来做查找,平均值跟矩阵中的数做对比,从上到下,从右到左,假如平均值大于等于矩阵的某一行的第N个值那么,那行就有N个数小于平均值,下一行就从第N个数开始比较,因为上一行的第N+1个数值比平均值大,下一行的肯定比平均值大,所以可以从第N个数开始;然后得到平均值比矩阵中的数大于等于的个数S,如果S大于等于K,最右边的数值R=平均值,否则,最左边的数值L=平均值+1;按照上述查找S的个数,然后和K比较,直到R不再大于L,输出L。
下面为部分流程的图解:
例子:[[1,3,5],[2,3,6],[4,5,7]],找第K=4个小的数
L:最左边的数值
R:最右边的数值
M:L和R的平均值
S:矩阵中小于M的个数
X:当前行最右边的位置
Y:当前行位置
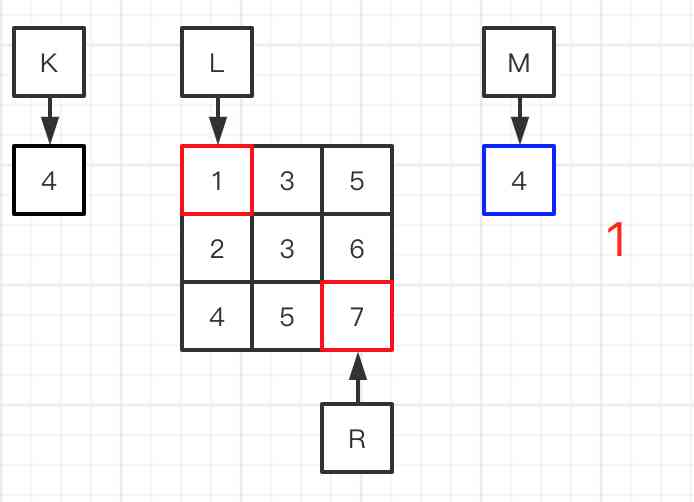
图一:初始化数据,L=1,R=7,计算出M=4
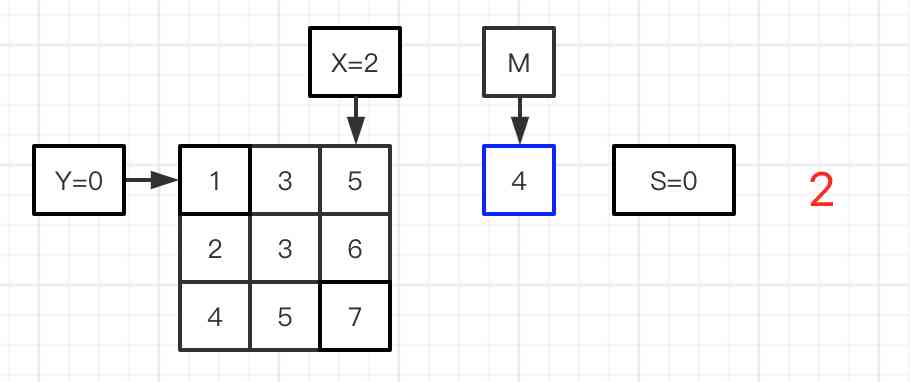
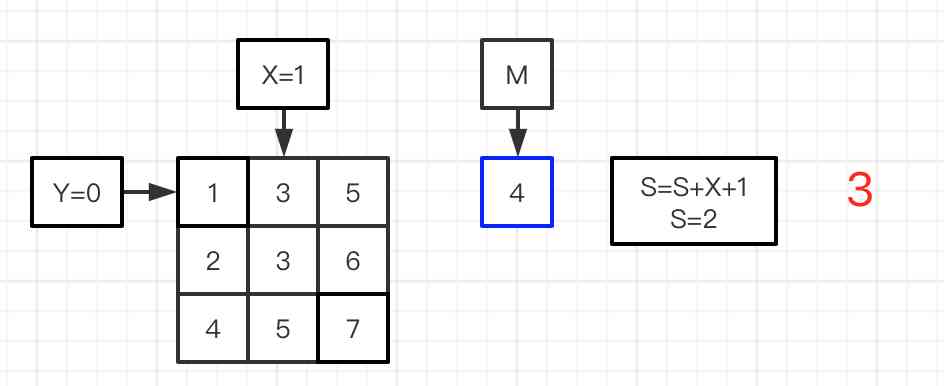
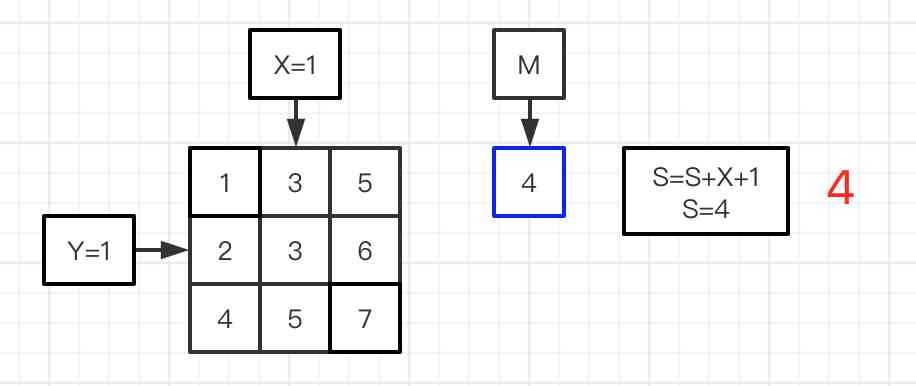
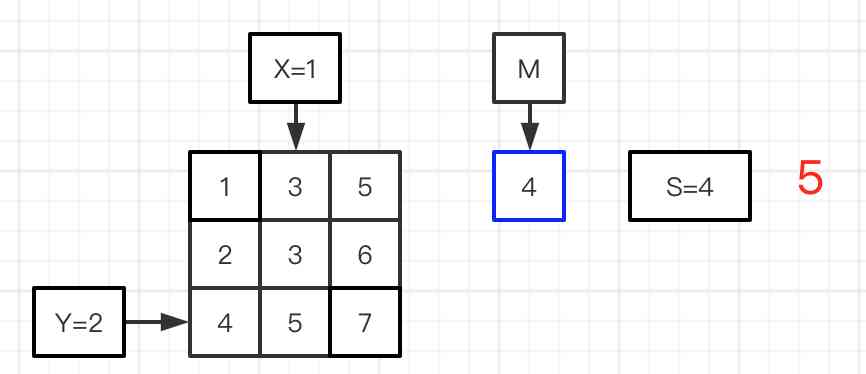
图二到六:进行平均值M与矩阵的数值做对比,图二的matrix[Y][X]=5比M=4大,X=X-1,比较前一位的数值;图三matrix[Y][X]=3比M=4小,则S加上第0行的个数,Y=Y+1,比较下一行;图四matrix[Y][X]=3比M=4小,则S加上第1行的个数,Y=Y+1,比较下一行;图五matrix[Y][X]=5比M=4大,X=X-1,比较前一位的数值;图六matrix[Y][X]=4与M=4相等,则S加上第1行的个数;完成矩阵的比较,得到最终的S。
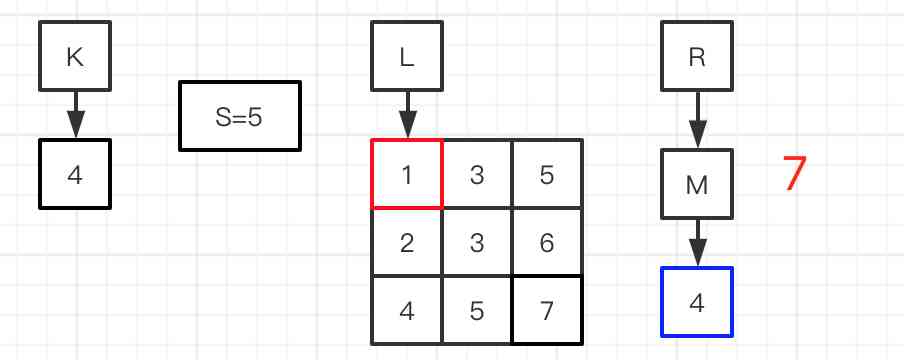
图七:S=5比K=4大,所以R=M=4
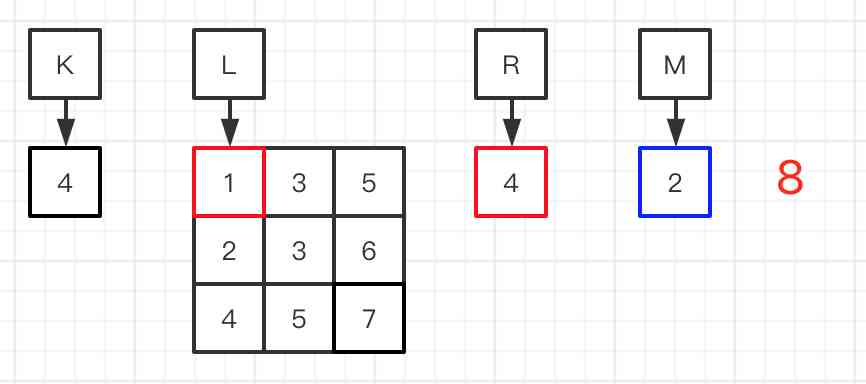
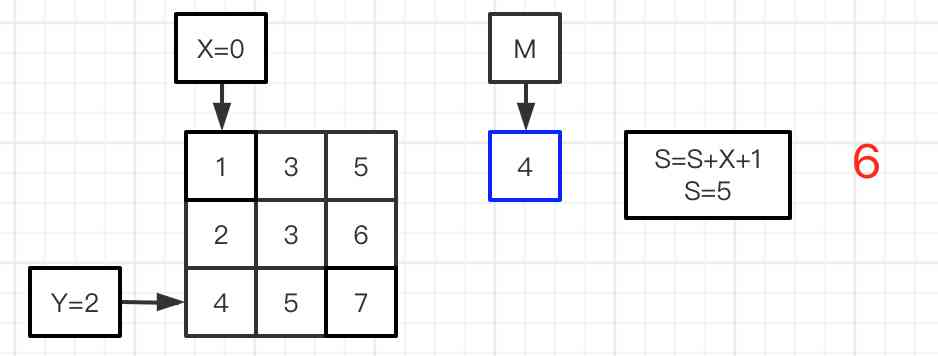
图八:计算出M=2,进行下一轮的比较,比较流程跟图二和六的做法一致,直到L大于等于R。
实现代码:
class Solution { public: int kthSmallest(vector<vector<int>>& matrix, int k) { int n = matrix.size(); int nm = n - 1; int nLeft = matrix[0][0]; int nRight = matrix[nm][nm]; while(nLeft < nRight) { int nMid = (nLeft + nRight) / 2.0; int nMaxx = 0; int nMaxy = nm; int nSize = 0; while(nMaxy >= 0 && nMaxx < n) { if(matrix[nMaxx][nMaxy] <= nMid) { nSize += (nMaxy + 1); nMaxx++; } else { nMaxy--; } } if(nSize >= k) { nRight = nMid; } else { nLeft = nMid + 1; } } return nLeft; } };
上面的步骤有一个问题需要讲解一下:为什么S大于等于K的时候R不是M-1,而是R=M?
因为当S==K的时候,有可能M就是等于矩阵中的某一个值,加入M-1就会导致答案错误。
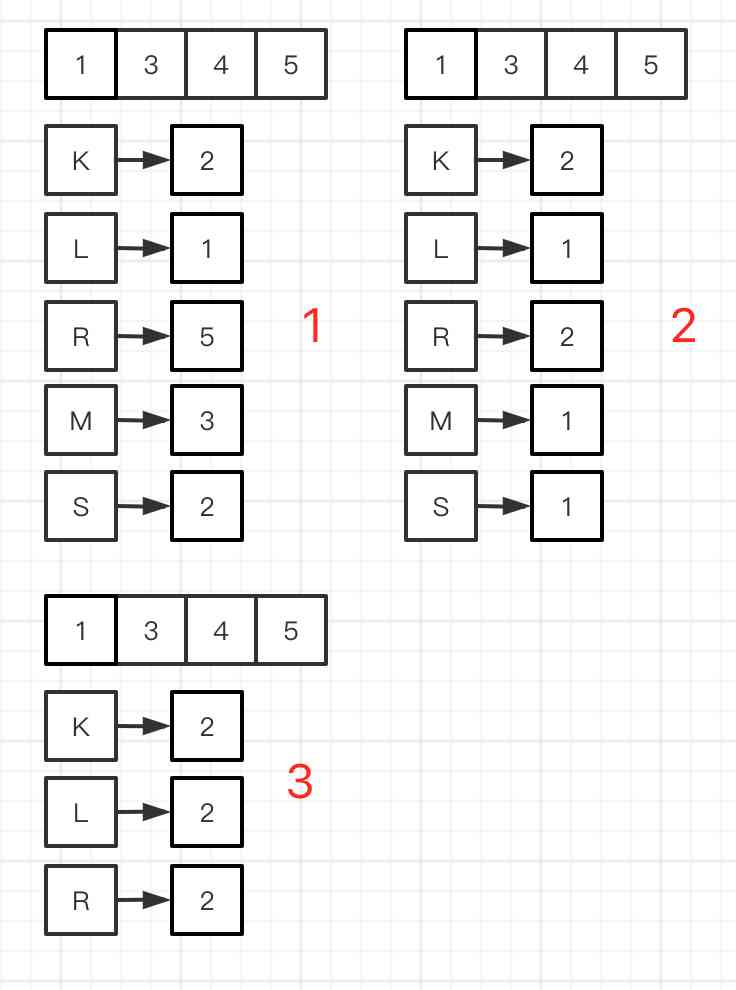
步骤1计算出S等于2,刚好跟K相等,M的值与数组中的也刚好相等,如果M-1的话R就等于2,然后最终结果就变成2。假如矩阵中有多个相同的值,S有可能大于K,M与要求的数相等,也会出现最后错误答案。L能加1的原因是,L的S个数比K要少,所以+1有可能变成S==K,直到L==R。

喜欢的可以关注公众号查看更多的文章