当前位置:网站首页>"Weilai Cup" 2022 Niuke summer multi school training camp 2
"Weilai Cup" 2022 Niuke summer multi school training camp 2
2022-07-26 19:24:00 【Bold!】
G.Link with Monotonic Subsequence
The question :
For each example , Give me a number n. from 1-n Form an arrangement . The value of an arrangement =max( The longest ascending subsequence , The length of the longest descending subsequence ), Output a sequence , Minimize the value of this arrangement .
Ideas :
Try to make the length of the longest ascending subsequence and the longest descending subsequence in an arrangement very small . One of our ideas is to first 1,2,```,n This sequence is grouped , Then arrange these groups in descending order , In that case , Because each group is strictly increasing , In this way, the length of the longest ascending subsequence can be controlled , And because the groups are arranged in descending order , In this way, the length of the longest descending subsequence can be controlled . in summary , Is the ascending order within the Group , Intergroup descending order . In fact, the minimum value obtained in the end is len=ceil(sqrt(n)).
So how to group ? How to divide each group ? How many are there in each group ?
What we want is to make the elements in each group len=ceil(sqrt(n)) individual , The number of elements in the last group <=len individual , Then arrange the groups in descending order . For example, an initial one is 1,2,3,4,5,6 Permutation ,
Then ensure that the maximum number of elements in the group is ceil(sqrt(6))=3 individual , Then it becomes [1,2,3][4,5,6] Two groups , Then arrange the groups in descending order , become [4 5 6] [1 2 3].
Code :
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline void solve(){
int n;
scanf("%d",&n);
double len=ceil(sqrt(n));
for(int i=n%int(len);i>=1;i--){// If you can't n average , Then first output the last remaining number
cout<<n-i+1<<" ";
}
for(int i=n/len;i>=1;i--){// Output in descending order is enough len Number of groups Group number : Descending
for(int j=1;j<=len;j++){
int x=(i-1)*len;// A number before the first number of each group
cout<<x+j<<" ";
}
}
cout<<endl;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t;
scanf("%d",&t);
while(t--){
solve();
}
return 0;
}
J.Link with Arithmetic Progression
The question :
Given length is n Array of a( Tell each number ai), I want to change these numbers to make this array an arithmetic sequence ai=a1+(i−1)d. Find out sum(ai’-ai)^2
Ideas :
Consider the least square method , Find the sum of squares of residuals .
namely x by 1-n, Corresponding y by a1-an, First find the fitting straight line , Then find out each x The point on the corresponding line , Then find the residual , Sum of squares of cumulative residuals .
Be careful :
You need to use the given in the title to input data .
You need to use long double To control accuracy , Otherwise it will be wrong .
Code :
#include <bits/stdc++.h>
#include <cstdio>
#include <cctype>
#include <vector>
namespace GTI{
char gc(void)
{
const int S = 1 << 16;
static char buf[S], *s = buf, *t = buf;
if (s == t) t = buf + fread(s = buf, 1, S, stdin);
if (s == t) return EOF;
return *s++;
}
int gti(void)
{
int a = 0, b = 1, c = gc();
for (; !isdigit(c); c = gc()) b ^= (c == '-');
for (; isdigit(c); c = gc()) a = a * 10 + c - '0';
return b ? a : -a;
}
}
using GTI::gti;
// using namespace GTI;
using namespace std;
typedef long long ll;
typedef long double ld;
using Parameter = struct {
ld k; // Slope
ld b; // intercept
};
// Least square calculation process
bool LeastSquares(std::vector<ld>& X, std::vector<ld>& Y, Parameter& param)
{
if (X.empty() || Y.empty())
return false;
int vec_size = X.size();
ld sum1 = 0, sum2 = 0;
ld x_avg = std::accumulate(X.begin(), X.end(), 0.0) / vec_size;
ld y_avg = std::accumulate(Y.begin(), Y.end(), 0.0) / vec_size;
for (int i = 0; i < vec_size; ++i) {
sum1 += (X.at(i) * Y.at(i) - x_avg * y_avg);
sum2 += (X.at(i) * X.at(i) - x_avg * x_avg);
}
param.k = sum1 / sum2;
param.b = y_avg - param.k * x_avg;
return true;
}
ld a[100005];
// The main function
int main(int argc, char* argv[])
{
int t;
// cin>>t;
t=gti();
while(t--){
ll n;
// cin>>n;
n=gti();// Input
Parameter param{ 0, 0 };
vector<ld> x_vec,y_vec;
for(int i=1;i<=n;i++){
// cin>>a[i];
a[i]=gti();// Input
x_vec.push_back(i);
y_vec.push_back(a[i]);
}
LeastSquares(x_vec, y_vec, param);
// printf("y=%lfx+%lf\n",param.k,param.b);
ld yi,ans=0;
for(int i=1;i<=n;i++){
yi=param.k*i+param.b;// To calculate the x Corresponding to y value
ans+=(yi-a[i])*(yi-a[i]);// Sum of squares of cumulative residuals
}
printf("%.15llf\n",ans);
}
}
K.Link with Bracket Sequence I
The question :
Give a length of n Parenthesized subsequence of a, Ask how many possible lengths are m Original sequence of .
Investigate :
Dynamic programming , string matching
Ideas :
Set a 3D array ,dp[i][j][k] Represents a string with a length of i, The matching length is j, The number of left parentheses is more than that of right parentheses k The answer is .
When it's an open parenthesis , You can match any .
When the right parenthesis is , Only when the number of left parentheses > The number of right parentheses can match .
Code :
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 210;
const int mod = 1e9+7;
int n,m,f[N][N][N];
char s[N];
void add(int &x,int y){// The reference , change x
x=(x+y)%mod;
}
inline void solve(){
scanf("%d%d%s",&n,&m,s+1);
// Initialize to 0
for(int i=0;i<=m;i++){
for(int j=0;j<=n;j++){
for(int k=0;k<=m;k++){
f[i][j][k]=0;
}
}
}
f[0][0][0]=1;// Initialize to 1
for(int i=0;i<m;i++){// Enumeration string length
for(int j=0;j<=n;j++){// Enumerate the length of successful matching
for(int k=0;k<=i;k++){// Enumerate the number of left parentheses more than right parentheses
// If it's left parenthesis , It can match at any time String length +1, The number of left parentheses is more than that of right parentheses +1
add(f[i+1][j+(s[j+1]=='(')][k+1],f[i][j][k]);
// Only when the number of left parentheses > When the number of right parentheses , Right parenthesis matching String length +1, The number of left parentheses is more than that of right parentheses -1
if(k) add(f[i+1][j+(s[j+1]==')')][k-1],f[i][j][k]);
}
}
}
// The answer is that the string length is m, The matching length is n, When the number of left parentheses and right parentheses is equal f value
printf("%d\n",f[m][n][0]);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t;
scanf("%d",&t);
while(t--){
solve();
}
return 0;
}
Link with Game Glitch
The question :
Find a maximum w, So that there is no loop .
Investigate :
graph theory , use Bellman-Ford The algorithm determines whether there is a negative ring
Ideas :
Consider drawing
Build points for each item , Each synthesis method consists of bi towards di There is an edge , The boundary right is ci/ai .
The original problem actually requires a maximum w , So that the edge weight on each side is multiplied by w after ,
There is no product greater than 1 Rings .
The most demanding w, Then you need a two-point answer ,check The problem of is similar to finding negative rings . Because the edge weight product is large , need
Take logarithm .
skill :
(1) If the number is too large, take logarithm
(2) If it's hard, it's hard , Take the opposite number and become negative edge weight , It is transformed into finding whether there is a negative loop .
Bellman-Ford The algorithm solves the negative edge weight problem
Code :
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1010,M=2010;
const double eps=1e-9;
// Build points for each item , Each synthesis method is from bi towards di There is an edge , The boundary right is ci/ai
int n,m,a[M],b[M],c[M],d[M];
double dis[N],w[M];
int Bellman_Ford(){
for(int i=1;i<=n;i++) dis[i]=0.0;//dis Array initializes vertices u The distance to each vertex , Initialize to 0
for(int i=1;i<n;i++){// Outer loop n-1 Time ,n Is the number of vertices
int f=0;
for(int j=1;j<=m;j++){// Inner loop m Time ,m Number of sides
// Relax the input edges in each round , to update dis Array
if(dis[b[j]]+w[j]<dis[d[j]]){
dis[d[j]]=dis[b[j]]+w[j];
f=1;// Circuit with negative weight
}
}
if(f==0) return 0;
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
}
double L=0.0,R=1.0;
while(R-L>eps){// Two points answer
double mid=(L+R)/2.0;
for(int i=1;i<=m;i++){
w[i]=-log(1.0*mid*c[i]/a[i]);// because mid And edge right c[i]/a[i] The product of may be very large , So take logarithm , Take the opposite number , It becomes to judge whether there is a negative ring
}
if(Bellman_Ford()==0) L=mid;
else R=mid;
}
printf("%.10lf\n",L);
return 0;
}
边栏推荐
- 2022 tea master (intermediate) examination question simulation examination question bank and answers
- 指标和标签是做什么的
- TB 117-2013美国联邦强制性法规
- Is it safe for CSC qiniu members to open preferential accounts? I don't know if it's the lowest Commission
- JS question brushing plan - array
- MySQL日志介绍
- Tensorflow GPU 1.15 installation
- 用低代码搭建千人食品制造企业高效管理系统案例分析
- EN 1504-6混凝土结构保护和修理用产品钢筋锚固—CE认证
- 【YOLOv5】--详细版训练自己的数据集 保姆级学习日志记录 手把手教程
猜你喜欢

PMP practice once a day | don't get lost in the exam -7.26 (including agility + multiple choices)

Support proxy direct connection to Oracle database, jumpserver fortress v2.24.0 release

LeetCode简单题之数组能形成多少数对
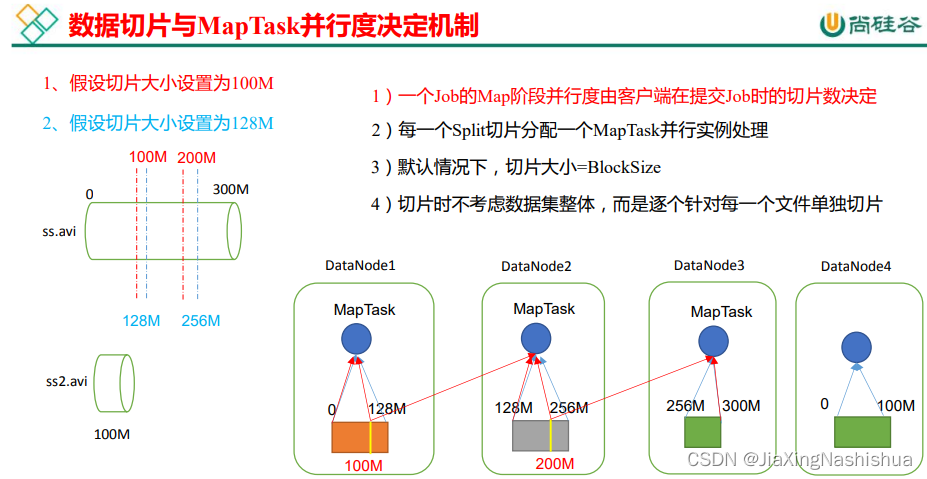
MapReduce (II)

一些时序建模策略(一)

Article 7:exited on desktop-dff5kik with error code -1073741511

How to become an excellent test / development programmer? Focus on planning and then move

Multi thread learning notes -1.cas

J3:Redis主从复制

多线程学习笔记-1.CAS
随机推荐
【MySQL必知必会】 日志Log详解
Leetcode simple question: the minimum total time required to fill a cup
[postgraduate entrance examination vocabulary training camp] day 14 - Panini, predict, access, apologize, sense, transport, aggregation
多线程学习笔记-1.CAS
JS map usage
LeetCode笔记:Biweekly Contest 83
销量下滑,品牌边缘化,失去“安全牌”的沃尔沃,还能走多远?
基础模块及算例#pytorch学习
机器学习笔记 - 构建推荐系统(6) 用于协同过滤的 6 种自动编码器
I'm cool, so I'm here
配置服务器环境
洋葱集团携手OceanBase实现分布式升级,全球数据首次实现跨云融合
Redis learning notes-2. Use of the client
[swoole series 3.1] have you been asked about processes, threads, and collaborations during the interview?
节省50%成本 京东云发布新一代混合CDN产品
2022 tea master (intermediate) examination question simulation examination question bank and answers
PMP每日一练 | 考试不迷路-7.26(包含敏捷+多选)
Detailed explanation of MySQL master-slave replication configuration
What aspects should be considered in the selection of MES system?
从6月25日考试之后,看新考纲如何复习PMP