当前位置:网站首页>ABC260 E - At Least One(双指针)
ABC260 E - At Least One(双指针)
2022-08-01 13:22:00 【Harris-H】
ABC260 E - At Least One(双指针)
一开始想到two pointers 了,但是不知道怎么快速维护是否满足条件。
原来开一个vector,然后用cnt变量存当前达到的组数。然后只对变为 0 0 0的桶影响cnt。
因为每个 i i i 对应的vector 至多遍历两次。
因此复杂度是: O ( n + m ) O(n+m) O(n+m)
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N, M;
cin >> N >> M;
vector<int> A(N), B(N);
for (int i = 0; i < N; i++) cin >> A[i] >> B[i];
vector<vector<int>> inv(M + 1);
for (int i = 0; i < N; i++) {
inv[A[i]].push_back(i);
inv[B[i]].push_back(i);
}
vector<int> cnt(N), ans(M + 3);
int cnt_zero = N;
for (int i = 1, j = 1; i <= M;) {
while (j <= M and cnt_zero != 0) {
for (auto& x : inv[j]) {
if (cnt[x] == 0) cnt_zero--;
cnt[x]++;
}
j++;
}
if (cnt_zero != 0) break;
ans[j - i]++, ans[M + 1 - i + 1]--;
for (auto& x : inv[i]) {
cnt[x]--;
if (cnt[x] == 0) cnt_zero++;
}
i++;
}
for (int i = 1; i <= M; i++) {
ans[i] += ans[i - 1];
cout << ans[i] << " \n"[i == M];
}
}
根据双指针,我们可以枚举左端点,右端点其实我们只需要更新 r = m a x ( r , m x [ l + + ] ) r=max(r,mx[l++]) r=max(r,mx[l++])
这里 m x [ v a l ] mx[val] mx[val] 是所有左端点为 v a l val val对应的最大右端点值。
显然 l + + l++ l++之后, r r r 必须大于等于 m x [ l ] mx[l] mx[l]。
特别地,当 l = 1 l=1 l=1, r r r 为所有左端点的最大值。这样 r r r是最小的 r r r。
然后双指针 O ( 1 ) O(1) O(1)更新即可。
注意 l ≤ min { b [ i ] } l\le \min\{b[i]\} l≤min{ b[i]} ,不然无解。
时间复杂度: O ( n ) O(n) O(n)
// Problem: E - At Least One
// Contest: AtCoder - AtCoder Beginner Contest 260
// URL: https://atcoder.jp/contests/abc260/tasks/abc260_e
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// Date: 2022-07-30 23:13:40
// --------by Herio--------
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e5+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7;
const int hashmod[4] = {
402653189,805306457,1610612741,998244353};
#define mst(a,b) memset(a,b,sizeof a)
#define db double
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define x first
#define y second
#define pb emplace_back
#define SZ(a) (int)a.size()
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define per(i,a,b) for(int i=a;i>=b;--i)
#define IOS ios::sync_with_stdio(false),cin.tie(nullptr)
void Print(int *a,int n){
for(int i=1;i<n;i++)
printf("%d ",a[i]);
printf("%d\n",a[n]);
}
template <typename T> //x=max(x,y) x=min(x,y)
void cmx(T &x,T y){
if(x<y) x=y;
}
template <typename T>
void cmn(T &x,T y){
if(x>y) x=y;
}
PII a[N];
int left_mx[N];
int is_right[N];
ll pre[N];
int n,m;
bool ck(int x){
for(int i=1;i<=n;i++){
if(x<a[i].x) return false;
}
return true;
}
int main(){
ll mn = 1e18;
cin>>n>>m;
rep(i,1,n){
cin>>a[i].x>>a[i].y;
cmx(left_mx[a[i].x],a[i].y);
cmn(mn,1LL*a[i].y);
}
int l=1,r=m,ans=0;
while(l<=r){
int mid = l+r>>1;
if(ck(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
//printf("%d %d\n",1,ans);
for(int i=1,j=ans;i<=mn;cmx(j,left_mx[i++])){
pre[j-i+1]++,pre[m-i+2]--;
}
rep(i,1,m) pre[i]+=pre[i-1];;
rep(i,1,m){
printf("%lld ",pre[i]);
}
return 0;
}
边栏推荐
猜你喜欢

PanGu-Coder:函数级的代码生成模型

态路小课堂丨浅谈优质光模块需要具备的条件!

如何使用OpenCV测量图像中物体之间的距离

MCU开发是什么?国内MCU产业现状如何

库函数的模拟实现(strlen)(strcpy)(strcat)(strcmp)(strstr)(memcpy)(memmove)(C语言)(VS)
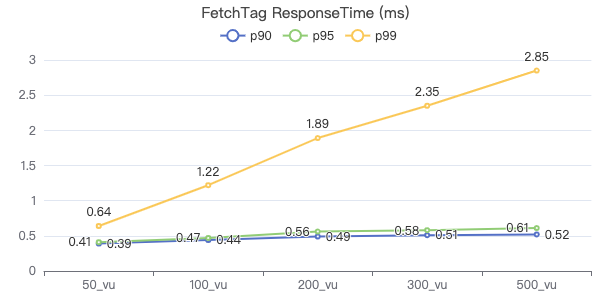
NebulaGraph v3.2.0 Performance Report

全球都热炸了,谷歌服务器已经崩掉了
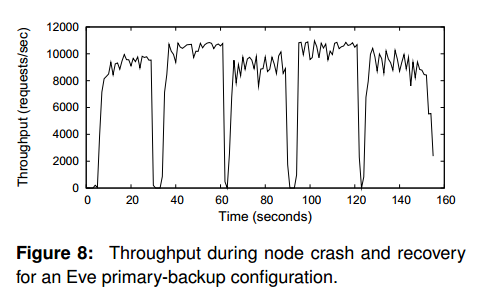
论文笔记All about Eve: Execute-Verify Replication for Multi-Core Servers

leetcode:1201. 丑数 III【二分 + 数学 + 容斥原理】
Efficiency tools to let programmers get off work earlier
随机推荐
Istio投入生产的障碍以及如何解决这些问题
iframe tag attribute description detailed [easy to understand]
uniapp读取和写入文件
8. How does the SAP ABAP OData service support the Create operation
CCS软件安装教程(超级详细)「建议收藏」
NebulaGraph v3.2.0 Performance Report
postgresql之page分配管理(一)
使用open3d可视化3d人脸
PAT 1163 Dijkstra Sequence(30)
mysql的基本使用
预防和制止家庭暴力 人身安全保护令司法解释今起施行
又拿三个大奖?!多力就是要让你吃的更营养更健康
全链路灰度在数据库上我们是怎么做的?
透过开发抽奖小程序,体会创新与迭代
NebulaGraph v3.2.0 性能报告
tensorflow2.0手写数字识别(tensorflow手写体识别)
Detailed explanation of table join
The obstacles to put Istio into production and how we solve them
JMP Pro 16.0 software installation package download and installation tutorial
论文详读《基于改进 LeNet-5 模型的手写体中文识别》,未完待补充