【图神经网络】图分类学习研究综述[2]：基于图神经网络的图分类

论文阅读：基于GNN的图分类学习研究综述

摘要：本文首先给出图分类问题的定义和该领域的挑战；然后梳理分析了两类图分类方法——基于图相似度计算的图分类方法和基于图神经网络的图分类方法；接着给出了图分类方法的评价指标、常用数据集和实验结果对比；最后介绍了图分类常见的实际应用场景，展望了图分类领域的未来研究方向并对全文进行总结。

关键词：图分类、图核、图卷积；图池化；图神经网络

---

3. 基于图神经网络的图分类

基于图核方法通常依赖于一组固定特征，其特征表示难以有效地适应于新的数据分布。本文重点关注基于图神经网络的图分类方法，这类方法通过端到端的方式进行模型的优化学习，为图分类的准确率带来了较大的提升。

应用于图像分类任务的传统卷积神经网络，主要包括卷积和池化两个操作，这两个操作依赖于图像数据的结构规则性和平移不变性。但不同于图像数据，图数据是非欧数据，同一个数据集中的每个图大小不同，结构不一。图中的每个节点也具有不同的局部结构，为图分类中卷积算子和池化算子的设计带来了巨大的挑战。

给定一组图，基于图神经网络的图分类方法通常先通过卷积的方式对这些图进行多次特征变换，然后在此基础上进行池化操作，将图的规模缩小，这个过程可以重复多次，最终得到整个图的表示，从而进行分类。

本节从卷积算子和池化算子的角度，对基于图神经网络的图分类方法进行总结和分析。利用图神经网络进行图分类的过程如图5所示，其中可选的操作和模块用虚线表示，环形箭头表示操作可以选择重复1-n次。

3.1 卷积

在图级别的任务中，图卷积操作主要是为了对图进行特征变换和特征提取，这个过程中需要尽可能多地利用图中节点特征和拓扑信息。当前在图分类任务中，主要的卷积方式有两种：
1）一种是信息传递（message-passing）式的卷积，即直接在原始图结构中定义由邻居聚合和迭代更新机制所组成的卷积算子。例如图卷积神经网络GCN，基于注意力机制的图卷积神经网络GAT等，
2）另一种是传统卷积网络（CNN）式的卷积，先将非欧图转化为规则网络结构，再应用传统卷积神经网络直接进行卷积操作。

（1）信息传递式卷积
Gilmer等提出了信息传递式（MPNN）的通用框架，将卷积过程形式化为信息传递和节点信息更新两个函数。信息传递是指各个节点将自己邻居的信息聚合到自身节点，节点信息更新是将该节点上一层的节点表示与聚合后的邻居信息进行结合的过程。本文把符合这种框架的卷积方式称为信息传递式（MPNN）卷积。
在图分类任务中，信息传递式卷积用来进行特征变换，得到图上节点的表示。以Kipf等提出的图卷积网络GCN为例：
$$H^{(l+1)}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$
其中，$H^{(l)}$是$l$层中节点的表示矩阵，$W^{(l)}$是可训练的参数矩阵，$\tilde{A}=A+I_N$表示包含自连接的邻接矩阵，$\sigma$表示非线性激活函数。

采用MPNN式卷积的图分类模型通常先利用节点的特征和图的结构求得特征映射后的节点表示，然后利用池化机制得到图的表示并进行分类。Ma等提出的谱池化（EigenPool）图分类模型，Gao等提出的Graph U-net模型和Lee等提出的自注意力池化（SAG）模型中均采用信息传递式卷积中的GCN进行节点表示学习。此外，Zhang等提出的深度图卷积网络DGCNN和Yuan等提出的结构池化图分类模型StructurePool也采用了类似于GCN的信息传递式卷积，具体卷积形式为$Z=f({\tilde{D}}_{-1}\tilde{A}XW)$，其中，$\tilde{A}$和GCN中定义相同，$\tilde{D}$是度矩阵，其中${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$。$W\in R^{c\times c^{\prime }}$是可训练参数矩阵。Zhang等证明了这种卷积方式理论上比GCN更近似于WL算法。Ying等提出的可微分池化分类模型DiffPool中，卷积部分可以采用任意MPNN式卷积。

以上提到的各模型中的MPNN式卷积，都是基于上文提到的1-WL算法提出的。但Xu等人指出，基于1-WL的任何信息传递式的图卷积神经网络，其表达能力都不会强于1-WL，而1-WL本身的表达能力有限，对很多非同构图并不能准确地分类。也就是说，当1-WL算法将两个非同构图判断为“可能同构”时，信息传递式的图卷积网络输出的两个图的表示是相同的。这样的弱区分能力，对图分类的效果会产生负面的影响。

近年来，有研究者提出了一些基于k-WL算法的图神经网络。k-WL算法是一种基于带标签子图的图同构判断算法。在基于1-WL的GNNs中，信息传递的基本单元是节点，不同于此，k-WL算法中信息传递的基本单元是大小为k的子图结构，其中，基于集合的k-WL算法set k-WL表达能力弱于k-WL算法，计算复杂度低于k-WL。考虑到内存的限制，Morris等人提出基于set k-WL算法的k-GNNs模型，该模型的关键是信息传递在大小为k的节点集合对应的子图结构之间进行。k-GNNs为每个大小为k的集合$s\in [V(G){]}^k$按照如下方式更新他们的特征向量：
$$f_k^{(t)}=\sigma \left\{f_k^{(t-1)}(s)\cdot W_1^{(t)}+\sum _{u\in N_L(s)\cup N_G(s)}{f}_k^{(t-1)}(u)\cdot W_2^{(t)}\right\}$$

其中，$N(s)=t\in [V(G){]}^k||s\cap t|=k-1$，表示集合s与邻居集合t的交集个数为k-1。k-GNNs的表达能力和set k-WL算法一样强大。该模型需要枚举大小为k的子图，由于计算复杂度较高，只考虑了k为1，2，3的情况，并提出一种层次化的1-2-3GNN网络。该模型在图分类任务中，取得了一致性好于1-GNN的效果。Maron等人提出通过矩阵相乘实现一种和3-WL有同样区分能力的GNN模型，比k-GNNs具有更低的空间复杂度和更容易部署的优点。

目前，图卷积神经网络模型的表达能力都是通过对图是否同构的判断能力来衡量的，那么基于k-WL算法的图卷积神经网络的表达能力显然强于基于1-WL算法的图卷积神经网络。然而，基于k-WL算法的图卷积神经网络需要带标签的子图结构进行枚举，类似于带标签信息的Graphlet的枚举，因此带来了非常大的计算代价。
（2）CNN式卷积
图分类任务中，还有一种卷积方式，即先把图数据按照一定的规则变换为欧式数据，然后按照传统方式进行卷积变换。本文把他们称为CNN式卷积。相比MPNN式卷积，这类卷积在目前的图分类中应用不多，但取得了较好的分类效果。
图分类中的CNN式卷积网络，可能也具备抽取图中关键结构的能力。Niepert等指出，由于图像中像素存在隐式的空间顺序，如图6a，因此可以为节点按照顺序从左到右从上到下生成邻居图，也就是感受野。接着，3×3的感受野读到的值会被转化为序列，然后送入卷积层中，如图6b所示。然而，图数据中每个节点结构并不一致，不存在这样统一的空间顺序。

Niepert等提出PSCN模型将非欧图数据转换为欧式数据，利用节点选择的方法解决了不同图数据中节点数不同的问题。具体地，用图标记算法按照某种排序标准对节点排序，使得不同图中结构相似的节点可以处在序列中相似的位置，然后选出指定个数的节点。接着，PSCN利用图标准化解决了图中每个节点的邻居个数不同导致的节点感受野定义问题。具体地，该模型先用宽度优先的方式聚合邻居并进行排序，将无序图空间映射到具有线性顺序的向量空间，接着在该序列中选择指定个数的节点作为中心节点的感受野。由于最优的图标准化是一个非常确定性多项式难（NP-hard）问题，PSCN并未解决这个问题，而是在众多图标记方法中选择了效果较好的方法并利用了辅助工具对邻居图中节点进行定序，得到统一的图表示后，用一维卷积层进行卷积，其中，卷积核大小与节点感受野大小相同。其余卷积和分类部分结构则可以任意选定。

由于PSCN模型为了解决不同图节点数不同的问题进行了节点的选择，因此对于节点的卷积过程无法进行层堆叠，只能抽取到一些局部的关键结构。直观的解释就是，如果进行第2次卷积，节点的感受野中的邻居节点有可能在第一次卷积前的节点选择中未被选中，因此没有这些节点的表达，无法进行第2次卷积，无法抽取一些全局的重要结构。针对这个问题，Tzeng等提出了以自我为中心的卷积网络Ego-CNN，可以发现图中的局部和全局关键结构。如图7是Ego-CNN的模型框架图。

不同于PSCN，以自我为中心的卷积网络Ego-CNN初始并没有进行节点的选择，而是将输入图中的所有节点经过一个网络嵌入算法得到图节点的初始表达。然后为每个节点选择指定个数的邻居并将邻居节点的表达拼接起来作为感受野。接着用与感受野尺寸相同的卷积核进行多层卷积。卷积过程可以公式化为：
$$H_{n,d}^{(l)}=\sigma (E^{(n,l)}\cdot W^{(l,d)}+b_d^{(l)})$$
$$E^{(n,l)}=[H_{n,:}^{l-1},H_{Nbr(n,1),:}^{(l-1)},...,H_{Nbr(n,K),:}^{l-1}{]}^T$$
其中，$E^{(n,l)}$是节点n在$l$层邻居的矩阵表示，由节点n及节点n的K个最近邻节点在上一层的表示连接形成，$Nbr(n,K)$表示节点n的第K阶最近邻居，它们是在模型开始前就确定好并且保持不变。$\sigma$是激活函数，$b_d$是偏置项。$\cdot$是Frobenius内积，定义为$X\cdot Y={\sum }_{i,j}{X}_{ij}{Y}_{ij}$。与PSCN相比，它们的卷积方式相同，主要的不同在于EgoCNN中节点k阶邻居的固定定义方式和多次卷积的堆叠。$H_{Nbr(n,K),:}^{(l-1)}$中已经包含了上一层的节点的表示，由于没有进行节点的选择，因此聚合K个最近邻时，没有PSCN中邻居节点表示可能不存在的问题。对$E^{n,l}$进行卷积时，可以重复地利用到上一层节点表示，因此，$l$层的Ego-CNN可以在以节点为中心$l-$跳的网络内发现重要结构，并可以通过反卷积的方式将关键结果可视化。

PSCN和Ego-CNN都是在节点上进行卷积，在卷积的过程中利用结构信息，不同于此，Peng等人提出的基于motif的子图注意力卷积网络MA-GCNN在将图表示为矩阵的过程中，就充分利用了图的结构信息。具体地，

• 在对图数据进行预处理时，该模型先按照某种选择策略选出N个节点，并为每个选出的节点选择K个重要的邻居节点形成N个子图。
• 然后将这些子图转换为基于motif匹配的矩阵表示，这个矩阵里的基本单元是一个2-跳路径的motif，经过匹配的多个motif形成子图表示，多个子图的表示连接形成整个图的表示。

可以看出，该模型在初始表示中用motif匹配的方式保留子图上的连边信息，也就是子图结构信息。基于此，MA-GCNN对这个矩阵进行2次感受野大小不同的卷积。然后利用子图级别的注意力机制，得到由重要子结构组成的图的表示进而进行分类。直觉上来说，在图分类中，子图级别的注意力机制更具有可解释性。通过验证表明，基于子图的卷积取得了更好的图分类效果，这也证明了该模型中对图数据的预处理过程更好地捕捉到了空间结构信息。
但与PSCN类似，MA-GCNN也对节点进行了排序和选择，节点选择的过程相当于一次池化操作，直接地丢掉了图中部分结构信息，节点排序操作则使得后续卷积得到的图上重要结构可能是这种启发式排序规则下的重要结构，而不是图分类任务所需要的重要结构。

对比这两类卷积方式，MPNN式的卷积假设相邻的节点标签相同，因此采用了邻居信息传递机制，这种机制从节点的角度出发，更适合图上节点级别的分类问题。CNN式卷积则具有发现关键结构的能力,这对于生物化学信息学等领域的实际应用具有重要意义.但当前CNN式卷积中存在参数过多,无法准确学习得到所有重要结构的问题.目前位置,关于图分类中适合的卷积方式并无定论,还不知道什么样的卷积方式可以最优地利用图中的结构信息帮助分类,接下来仍然需要探索.

3.2 池化

传统卷积网络中的池化也被称为下采样,可以降低特征维度,减少参数量并扩大感受野.作为欧式数据,图像数据中不同像素点的结构统一,因此传统卷积神经网络中的池化算子考虑结构信息时的方式会比较简单直观,主要有最大池化,加和池化和均值池化等方法.

在图分类中,池化操作主要是配合某些类型的卷积操作,降低表示的维度,得到整个图的表示.

不同于图像数据,在图数据中,每个节点的局部结构不同,在对图数据节点表示进行池化时,需要考虑每个节点不同的局部结构信息.

池化是图粗化的过程, 把相似的节点聚类在一起, 因此需要在图上定义有意义的邻居. 池化一般包括两个步骤:

1. 第一步,求分配矩阵,分配矩阵决定哪些邻居聚类在一起形成聚类簇. 分配矩阵$S^{(l)}\in R^{n_l\times n_{l+1}}$是第$l$层节点分配到$l+1$层不同的聚类簇中的指示矩阵.矩阵的行表示节点,共有$n_l$个.列表示粗化后的聚类簇,共有$n_{l+1}$个.
2. 第二步,按照分配矩阵进行聚合,即选定聚类簇中节点的聚合方式并将每个聚类簇聚合为一个新的超节点,所有的超节点构成新的图.通常在最直接的聚合方式下,新图的特征矩阵由$X^{(l+1)}=S^{(l)T}{X}^{(l)}$得到,邻居矩阵由$A^{(l+1)}=S^{(l)T}{A}^{(l)}{S}^{(l)}$得到. 当然,很多模型会提出新的更复杂的聚合方式.

本小节从分配矩阵的角度对图分类领域池化方法进行分类,并对具体的分配和聚合方式进行介绍分析.

(1) 节点硬分配和聚合
节点硬分配的方式是将图上的节点分为若干个无重叠的簇. 具体地, 硬分配矩阵是指从行的角度来说, 每一行有一个值为1,其他值均为0的分配矩阵.意味着每个节点属于且仅属于一个聚类簇. Ma等人提出的谱池化(EigenPooling)利用谱聚类得到硬分配矩阵$S^{(l)}$, 并根据该矩阵进行子图划分. EigenPooling将整个图划分为一些没有重叠节点的子图(聚类簇), 并把每个子图当作一个超节点.其中超节点之间的邻接矩阵通过$A^{(l+1)}=S^{(l)T}{A}^{(l)}{S}^{(l)}$得到. 子图中节点进行聚合时,EigenPooling并不是直接把分配矩阵$S^{(l)}$当做池化算子,而是将子图特征分解后得到的特征向量组合形成多个池化算子. 接着, 超节点的表示可以利用池化算子${\Theta }_l$通过$X_l={\Theta }_l^{T}X$得到, 多个池化算子得到的多组超节点表示并进行拼接后, 得到最终的超节点表示. 从局域角度来看, 这样的池化过程是子图上图信号的傅里叶变换过程; 从全局的角度来看,这样的池化算子相当于滤波器, 池化的过程就是对图上信号进行滤波, 这些池化算子保留了很好的性质, 如可以完好恢复图上信号,最大程度保留图上信息. 图8展示了利用信息传递式的图卷积算子和EigenPooling的池化算子进行图分类的过程.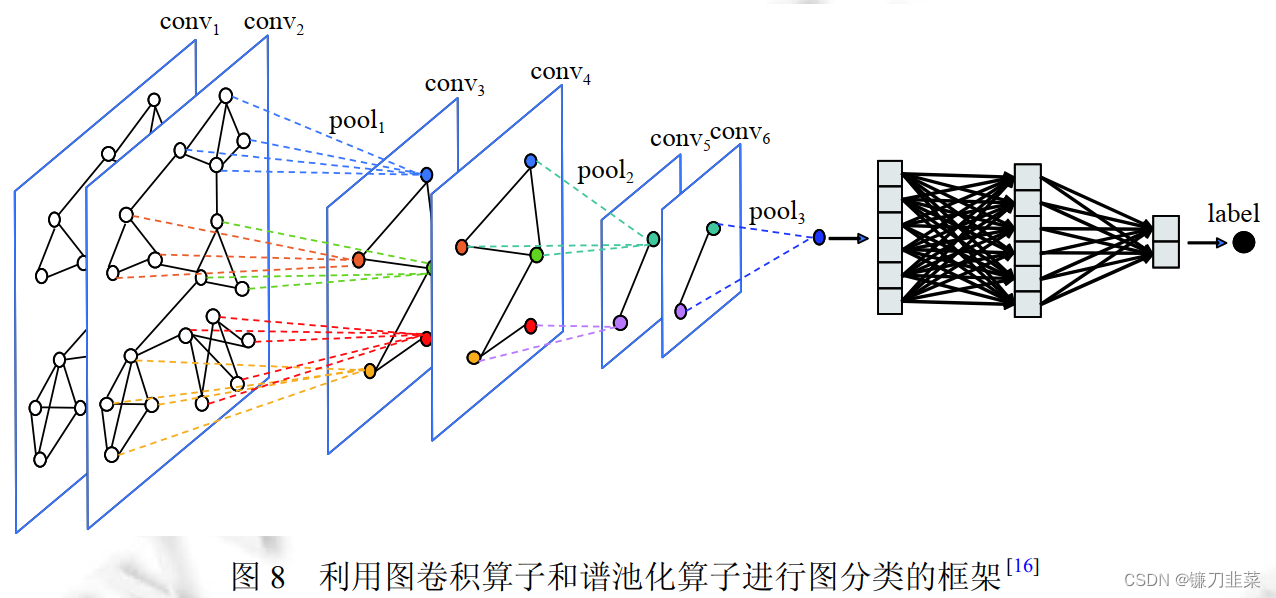

Wu等人则认为度相同的节点可能有相似的结构信息,为了保留度相关的节点结构信息,他们提出了度特定的图神经网络模型(DEMO-Net).该模型在池化过程中, 将度相同的节点聚合为一个新的超节点并采用了表示拼接的聚合方式, 也属于基于硬分配矩阵的池化.

Diehl等人提出的EdgePool通过学习边的分数来决定哪两个节点聚合在一起. 具体地, 在进行池化时, EdgePool先为边打分并排序,然后选择分数最高的边将其两端的节点聚合在一起形成新的虚拟节点. EdgePool中没有显式地给出分配矩阵,但这个过程属于节点硬分配的池化.

此外,值得注意的是,一些简单的置换不变(permutation invariant)函数(例如加和池化, 最大池化等),也属于特殊的基于节点硬分配的池化方式.

基于节点硬分配的池化模型中,在得到节点表示后,一般按照图聚类或者特定规则将节点聚合为簇, 每个节点属于且仅属于一个簇. 这种池化方式得到的图表示很大程度上依赖于节点聚合规则, 在某些场景下, 可能存在节点聚合规则与分类任务适配不够好的情况, 从而影响图分类的效果.

(2) 节点软分配与聚合
节点软分配的方式是将图上的节点分为若干个可能有重叠的簇,也就是每个节点不仅属于一个簇.具体地,软分配矩阵是指从行的角度来看,行中每个值的取值范围为$0\le p_{ij}<1$,表示节点$i$以概论$p_{ij}$属于第$j$个簇 . Ying等人提出的可微分池化(DiffPool)模型就是通过参数学习的方式得到软聚类分配矩阵$S^{(l)}$. 模型框架如图9所示,模型中包含两个图神经网络,一个嵌入图神经网络用来学习节点在$l$层的表示:
$$Z^{(l)}=GN{N}_{l,embed}(A^{(l)},X^{(l)})$$,
另一个池化图神经网络用来学习软分配矩阵:
$$S^{(l)}=Softmax(GN{N}_{l,pool}(A^{(l)},X^{(l)}))$$.

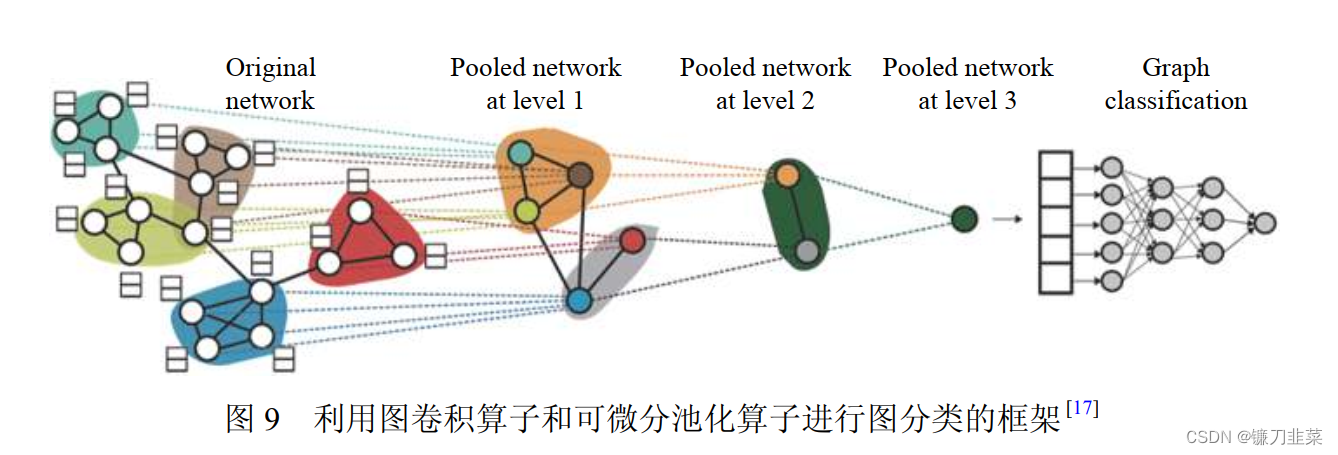
得到$l$层的节点表示和软分配矩阵后,通过$X^{(l+1)}=S^{(l)T}{X}^{(l)}$和$A^{(l+1)}=S^{(l)T}{A}^{(l)}{S}^{(l)}$分别得到粗化图的节点表示和邻接矩阵.该模型通过学习的方式得到软分配矩阵,仅使用图分类任务返回的梯度信号很难训练好可微分池化图神经网络,因此很难学习到好的软分配矩阵.

为了克服这个问题,在模型的训练过程中加入一个辅助的链路预测任务,假设临近节点应该被池化在一起.此外,为了确保每个聚类簇中的元素是确定的,该模型还对学得的软分配矩阵进行限制,使得每一行尽量靠近one-hot向量(每行只有一个1,其他都是0的向量). 可微分池化模型第一次提出通过学习的方式利用结构信息和特征信息得到分配矩阵,但实际应用中学习到好的分配矩阵难度较大,且由于软分配矩阵比较稠密,导致模型计算复杂度较高.

DiffPool的目标是学习得到一个软分配矩阵进行图分类,不同于此, Amir等人提出基于记忆层的图神经网络,目标是通过学习的方式得到多种分配方式,然后利用卷积将多个分配矩阵聚合为一个最终的分配矩阵,用于池化.这种学习多个分配矩阵的方式有效地提升了模型能力,取得了较好的分类效果.

对比前文介绍的基于节点硬分配的池化方法,基于节点软分配的池化不要求每个节点唯一的属于一个簇,这种宽松的限制更符合实际场景中的情况,每个节点可能同时在多个簇中扮演角色.此外,在目前的基于节点软分配的池化方法中,通常都采用了学习的方式来得到分配矩阵,通过端到端优化在任务依赖的场景中取得了较好的效果.

(3)节点选择与聚合
基于节点选择的池化方法是指从图中选择一些节点来代表整个图,其中被选出的每个节点都代表一个簇. 一般来说,节点选择型分配矩阵在每一列中有一个值为,其他均为0.也就是在$n_l$个节点中选择$n_{l+1}$个节点作为粗化后图节点. 这类方法的核心在于设计一种为节点打分和选择节点的方式. Lee等人首先提出了基于自注意力的池化(SAGPool)模型, 该模型在进行池化是,同时考虑了节点特征和图拓扑信息. 具体地, SAGPool利用图卷积网络为每个节点学得一个自注意力分数,这个分数表示节点在图中的重要性:
$$Z=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X{\Theta }_{att})$$
其中, $Z\in R^{N\times 1}$, $\tilde{A}$的定义和GCN中相同, ${\Theta }_{att}\in R^{F\times 1}$是SAGPool模型中唯一的参数. 得到节点重要性分数降序排列, 按照排序结果保留一定比例的重要节点, 当作粗化图的节点:
$$idx=top-rank(Z,[kN]),Z_{mask}=Z_{idx}$$,
其中, top-rank函数返回值最大的[kN]个节点的标号idx, 在进行池化时,保留被选择的重要节点的节点特征和它们之间的连接方式:
$$X^{\prime }=X_{idx,:},X_{out}=X^{\prime }\odot Z_{mask},A_{out}=A_{idx,idx}$$,
其中, $X_{out}$和$A_{out}$是池化后图的节点特征矩阵和邻接矩阵. 图10 给出了SAGPool的结构示意图.

Gao等人提出GraphU-Net模型,借鉴图像中的U-Net模型思想, 该模型包括图上的池化算子gPool和上采样算子gUnpool. 其中, 池化算子gPool也采用了节点选择的方式进行, 与SAGPool的主要不同在于节点的选择策略. 具体地, 该模型利用一个可训练的映射向量p, 把所有的节点特征映射到一个1维标量, 这个标量大小代表节点中可以保留下来的信息的多少. 为了尽可能多地保留原图中的信息,模型选择了那些标量值较大的对应节点来组成新图. 计算过程如下:
$$y=\frac{X^l{p}^l}{||p^l||},idx=rank(y,k),\tilde{y}=Sigmoid(y(idx))$$
其中, y向量的值表示每个节点在p上可以保留的信息多少. $\tilde{y}$中提取出了被选择节点中可以保留信息比例的值. idx表示被选择出的节点标号. 选出节点后, 用类似SAGPool的方式, 保留被选择节点的连接方式作为新图的邻接矩阵, 并按照比例保留节点特征作为新图的特征矩阵.

Cangea等人也利用了GraphU-Net的节点选择策略进行图池化. Ranjan等人为了解决:(1)DiffPool不能应用于大图; (2)GraphU-Net等池化方法对结构信息的利用不够充分的问题, 提出了自适应的结构感知池化方法(ASAP), 该方法先将每个节点当作聚类中心进行局部聚类形成簇, 然后提出一种卷积方法对这些簇打分并排序, 选择分数最高的[kN]个簇形成池化后的图. 实际上节点聚类形成簇的过程中, 簇的个数等于节点个数, 簇的表示相当于加入邻居信息的节点表示. 因此, 整体上看, ASAP的池化过程属于基于节点选择的池化.

这些基于节点选择的图池化方法中存在一些问题:

1. 节点选择策略的角度单一,缺少目标性;
2. 未被选中的节点特征直接被丢弃, 特征信息未利用充分;

Zhang等人提出了一种基于结构和特征的图自适应池化方法. 该方法提出了新的节点选择策略, 包括两个分别从结构,特征方面对节点的重要性进行排序的模块和一个综合结构和特征信息的排序模块. 除此之外, 该模型在节点选择之前,对所有节点信息进行聚合, 使得池化后的图中节点不仅包含被选中的节点信息,也包含被丢弃节点的信息. 这个模型在一些生物数据集上取得了较好的分类效果.

不同于其他方法, Zhang等人提出的结构学习的层次图池化方法中,给出了意义明确的节点选择策略, 他们认为, 当一个节点可以由它的邻居节点们计算得到时, 意味着该节点在池化图上可以被删掉, 并且不会带来信息损失. 这个非参的池化算子在多个图分类数据集上取得了较好的分类效果, 证明了这种节点选择策略的有效性.

在目前的分类任务中, 将池化方法分成了:

1. 基于节点硬分配,
2. 基于节点软分配
3. 基于节点选择的池化.

从另一个角度看,所有图上的池化方法又可以分为两类:一类是全局池化, 得到节点表示后,做一次池化得到整个图的表示, 如DGCNN. 另一类是层次池化, 在每个卷积层后面, 进行不同规模的池化以缩小图的尺寸,最终得到整个图的表示, 如DiffPool, SAGPool.

由于卷积中节点沿着图的边进行信息传递, 得到的节点表示是平的, 通过层次池化, 可以得到层次化的图的表示. 层次池化方法的效果在很多模型中得到了验证. 表3对当前基于图神经网络的图分类方法进行总结和对比.

---

下一节:图分类方法评价及图分类应用