当前位置:网站首页>Detailed explanation of Fisher information quantity detection countermeasure sample code
Detailed explanation of Fisher information quantity detection countermeasure sample code
2022-07-04 13:54:00 【PaperWeekly】

PaperWeekly original · author | guiguzi

introduction
In the last article 《Fisher The application of information quantity in countermeasure samples 》 It elaborates on Fisher The amount of information is fighting attacks , defense , And the application in detection , And analyzed three representative papers .Fisher The amount of information is a very good mathematical tool that can be used to explore the deep causes of the antagonism behavior of the deep learning model .
This article is mainly based on Fisher A paper on information quantity to detect countermeasure samples 《Inspecting adversarial examples using the Fisher information》 Code for deep parsing , In this paper, three indexes are proposed to detect the countermeasure samples Fisher Information matrix trace ,Fisher Information quadratic form and Fisher Information sensitivity . This paper will supplement the intermediate proof process of the results directly given in the paper , And some important key details in the code will also be explained in the corresponding chapters .

Fisher Information matrix trace
Given input samples , The output of the neural network is Dimensional probability vector , On the parameters of neural network Of Fisher The continuous and discrete forms of the information matrix are as follows :
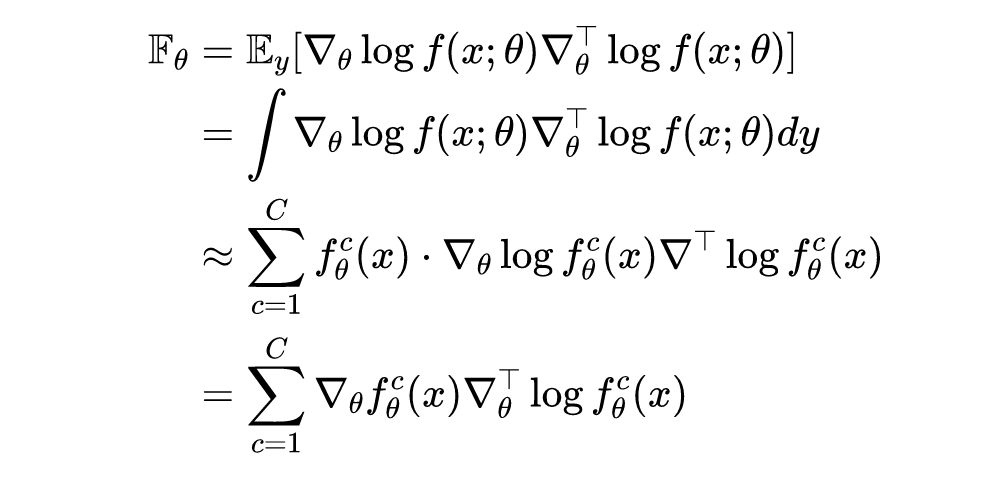
It can be seen that ,,. It should be noted that , Calculate a very small-scale neural network ,Fisher The amount of computation of the information matrix It's also tricky , What's more, those neural networks that often have hundreds of millions of parameters , The amount of calculation is much larger . Because the purpose of the original paper is to only focus on the detection of countermeasure samples , No detailed calculation is required Fisher Each exact value in the information matrix , Given the sample Fisher A value range of information quantity can be used as an indicator of detection , So... Is used in the paper Fisher The trace of the information matrix is used as the detection index , The specific calculation formula is as follows :
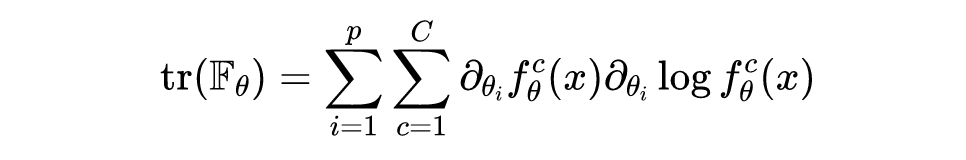
You should know that there are always some differences between theoretical analysis and practical programming , In the derivation of the above formula , It considers all the weight parameters in the neural network as a one-dimensional parameter vector , But in actual programming , The parameters of neural network are sorted by layers , But when it comes to solving Fisher The amount of information , The two cases are consistent . Suppose there is a neural network with four hidden layers , The parameters are , Then the corresponding parameters and gradients are as follows :
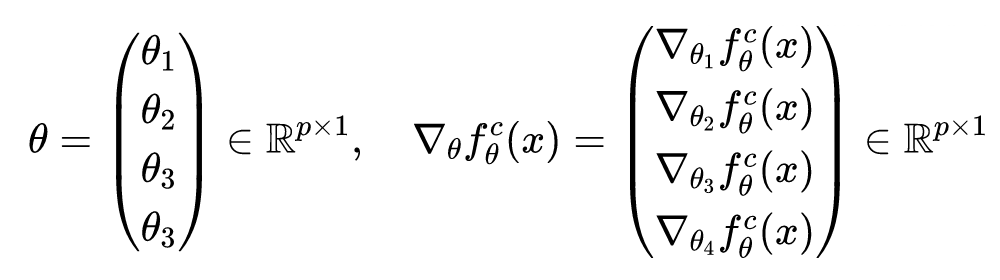
It is further known that in two cases Fisher The traces of the information matrix are equal :
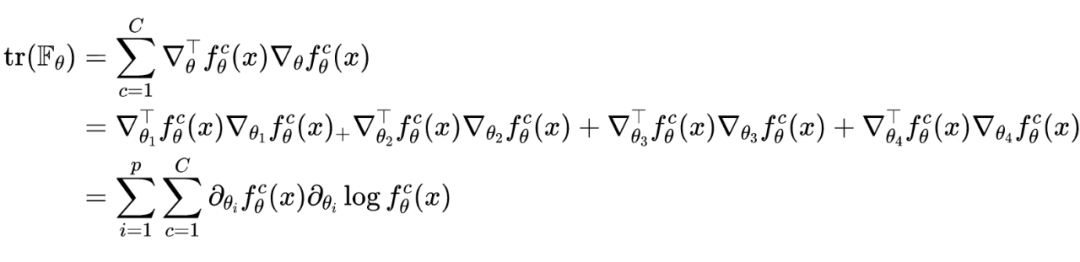
At this point, it can be found that back-propagation calculation Fisher The calculation amount of the trace of the information matrix is , Far less than the calculation Fisher The amount of computation of the information matrix .

Fisher Information quadratic form
matrix The trace of can be written as , among Is the unit vector , That is to say Elements are , The rest of the elements are , This can be understood as The average value of divergence for each parameter change . Inspired by this , Authors can choose a specific direction and measure , Instead of finding the average value on the basis of complete orthogonality , There is the following quadratic form :
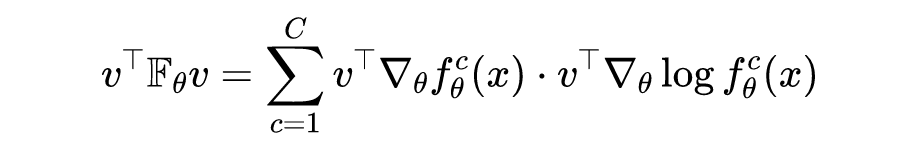
Where the given vector With the parameters And data points of :
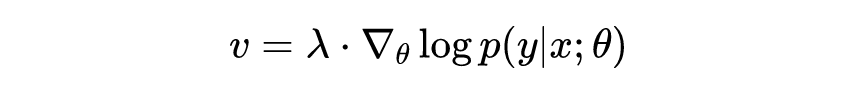
When the When normalizing , Then there is the following quadratic form :
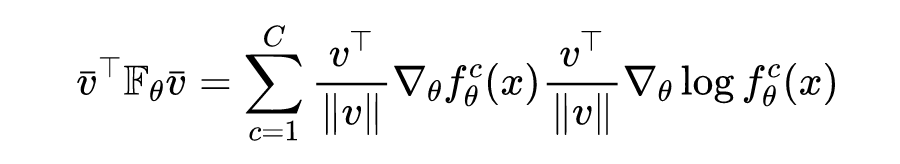
It should be noted that the selected direction is not unique , If you want to maximize the value of the quadratic form , It is Fisher The maximum eigenvalue of the matrix , The selected direction is the eigenvector corresponding to the maximum eigenvalue . It should be pointed out that ,Fisher The trace of the matrix must be greater than Fisher The maximum eigenvalue of the matrix , The specific proof is as follows :
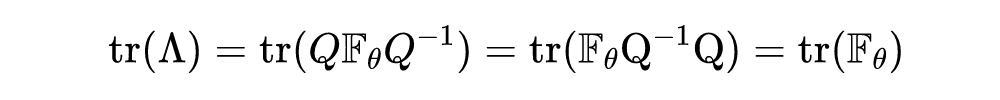
among For matrix Characteristic diagonal matrix of , Is a unit orthogonal matrix . In actual programming , To simplify the calculation , Will use the finite difference calculation to estimate the result of the back propagation gradient , According to Taylor's formula :
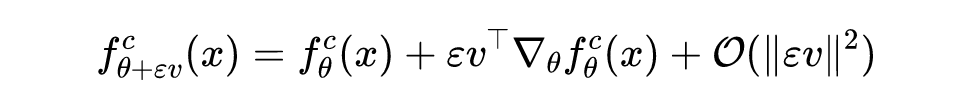
Then there are :
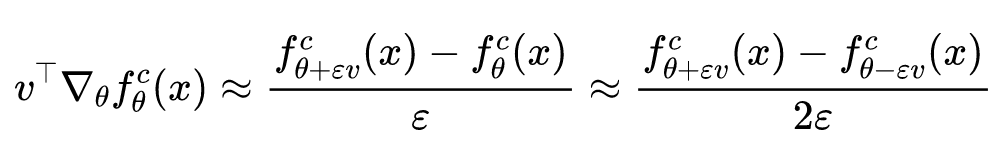

Fisher Information sensitivity
In order to further obtain available Fisher The amount of information , The author randomly introduces a single random variable into the input sample , That is to say :
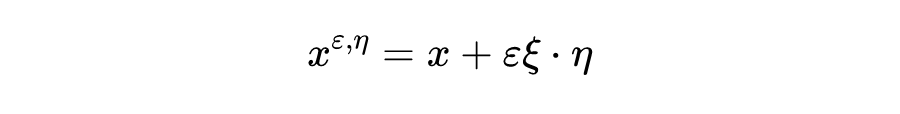
among , also And They have the same dimensions . For this perturbed input , For its Fisher The information matrix is :
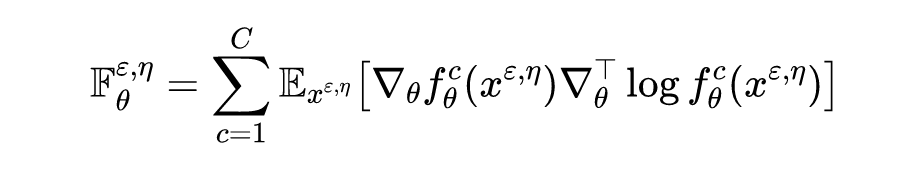
among , The... Of the matrix That's ok , The first The elements of a column can be expressed as :
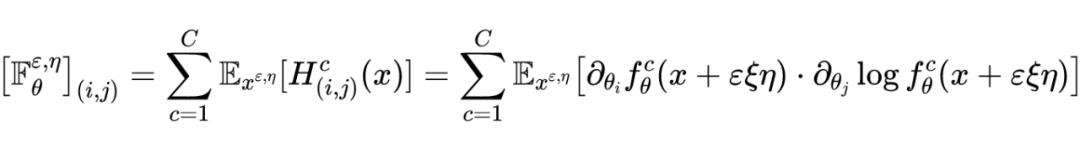
Again because Of the That's ok , The first The elements of the column are :
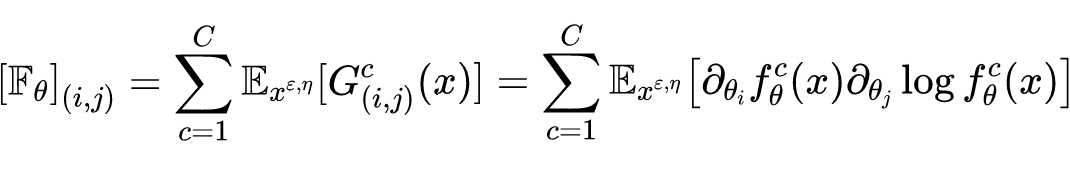
Then there is the Taylor expansion :
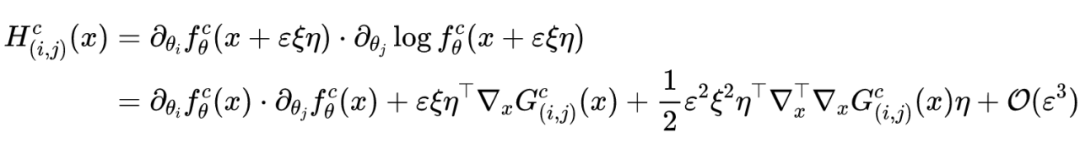
The second term of the above formula The matrix can be expressed as :
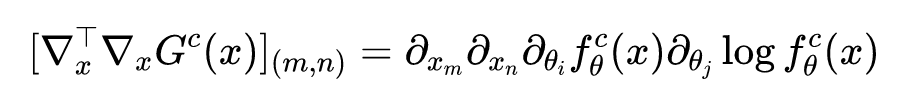
Again because Is an average of , The variance of Random variable of , Then there are :
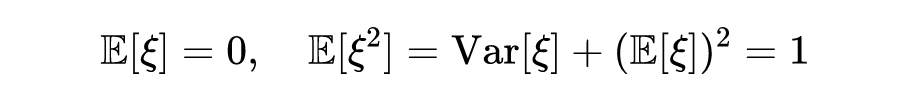
Based on the above derivation results , Then there are :
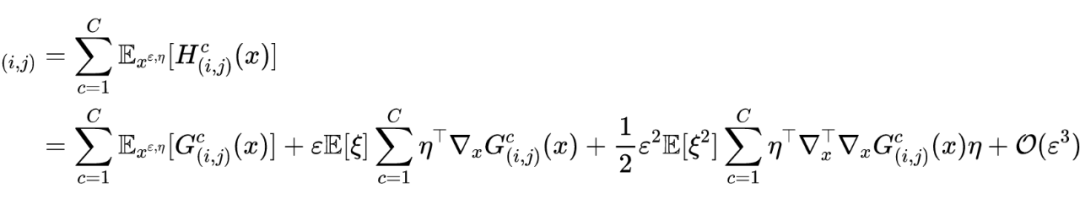
Finally, we can get the same result as in the paper :
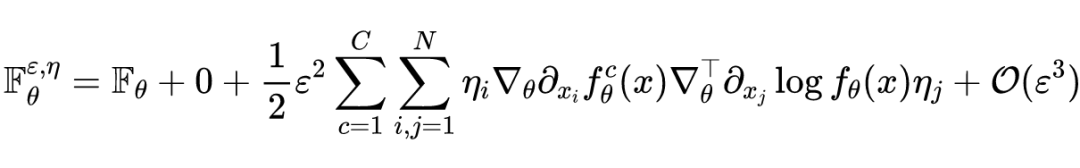
As in the previous section Fisher Matrix quadratic form , The authors also study the perturbed samples Of Fisher Finding quadratic form of matrix , Then there are :
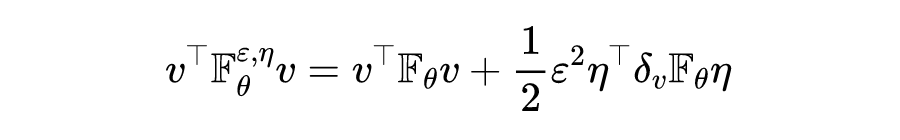
among :
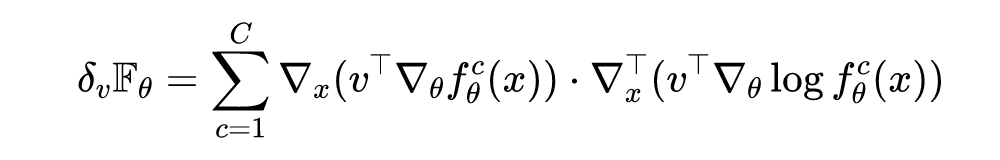
Let's say that a given perturbation vector It's the unit vector , namely . In practical programming, the finite difference method is used to estimate the result of anti back propagation gradient , Then there are :
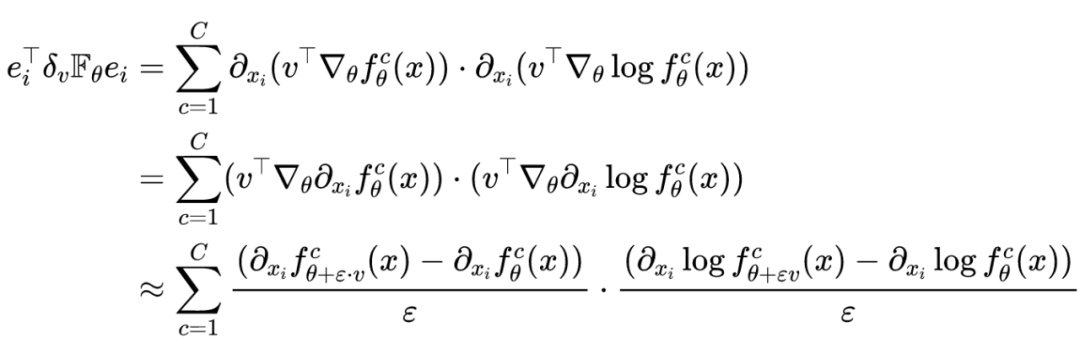
The above formula is called Fisher Information sensitivity (FIS), It is mainly used to evaluate the Importance of input nodes .

Code example
Fisher Trace of information matrix ,Fisher Information quadratic form and Fisher The code examples and experimental results of information sensitivity are as follows , Corresponding to the principle introduction above , You can better understand the implementation details of the relevant principles in the code examples .
import torch
import torch.nn.functional as F
from copy import deepcopy
class FISHER_OPERATION(object):
def __init__(self, input_data, network, vector, epsilon = 1e-3):
self.input = input_data
self.network = network
self.vector = vector
self.epsilon = epsilon
# Computes the fisher matrix quadratic form along the specific vector
def fisher_quadratic_form(self):
fisher_sum = 0
## Computes the gradient of parameters of each layer
for i, parameter in enumerate(self.network.parameters()):
## Store the original parameters
store_data = deepcopy(parameter.data)
parameter.data += self.epsilon * self.vector[i]
log_softmax_output1 = self.network(self.input)
softmax_output1 = F.softmax(log_softmax_output1, dim=1)
parameter.data -= 2 * self.epsilon * self.vector[i]
log_softmax_output2 = self.network(self.input)
solfmax_output2 = F.softmax(log_softmax_output2, dim=1)
parameter.data = store_data
# The summation of finite difference approximate
fisher_sum += (((log_softmax_output1 - log_softmax_output2)/(2 * self.epsilon))*((softmax_output1 - solfmax_output2)/(2 * self.epsilon))).sum()
return fisher_sum
# Computes the fisher matrix trace
def fisher_trace(self):
fisher_trace = 0
output = self.network(self.input)
output_dim = output.shape[1]
parameters = self.network.parameters()
## Computes the gradient of parameters of each layer
for parameter in parameters:
for j in range(output_dim):
self.network.zero_grad()
log_softmax_output = self.network(self.input)
log_softmax_output[0,j].backward()
log_softmax_grad = parameter.grad
self.network.zero_grad()
softmax_output = F.softmax(self.network(self.input), dim=1)
softmax_output[0,j].backward()
softmax_grad = parameter.grad
fisher_trace += (log_softmax_grad * softmax_grad).sum()
return fisher_trace
# Computes fisher information sensitivity for x and v.
def fisher_sensitivity(self):
output = self.network(self.input)
output_dim = output.shape[1]
parameters = self.network.parameters()
x = deepcopy(self.input.data)
x.requires_grad = True
fisher_sum = 0
for i, parameter in enumerate(parameters):
for j in range(output_dim):
store_data = deepcopy(parameter.data)
# plus eps
parameter.data += self.epsilon * self.vector[i]
log_softmax_output1 = self.network(x)
log_softmax_output1[0,j].backward()
new_plus_log_softmax_grad = deepcopy(x.grad.data)
x.grad.zero_()
self.network.zero_grad()
softmax_output1 = F.softmax(self.network(x), dim=1)
softmax_output1[0,j].backward()
new_plus_softmax_grad = deepcopy(x.grad.data)
x.grad.zero_()
self.network.zero_grad()
# minus eps
parameter.data -= 2 * self.epsilon * self.vector[i]
log_softmax_output2 = self.network(x)
log_softmax_output2[0,j].backward()
new_minus_log_softmax_grad = deepcopy(x.grad.data)
x.grad.zero_()
self.network.zero_grad()
softmax_output2 = F.softmax(self.network(x), dim=1)
softmax_output2[0,j].backward()
new_minus_softmax_grad = deepcopy(x.grad.data)
x.grad.zero_()
self.network.zero_grad()
# reset and evaluate
parameter.data = store_data
fisher_sum += 1/(2 * self.epsilon)**2 * ((new_plus_log_softmax_grad - new_minus_log_softmax_grad)*(new_plus_softmax_grad - new_minus_softmax_grad))
return fisher_sum
import torch
import torch.nn as nn
import fisher
network = nn.Sequential(
nn.Linear(15,4),
nn.Tanh(),
nn.Linear(4,3),
nn.LogSoftmax(dim=1)
)
epsilon = 1e-3
input_data = torch.randn((1,15))
network.zero_grad()
output = network(input_data).max()
output.backward()
vector = []
for parameter in network.parameters():
vector.append(parameter.grad.clone())
FISHER = fisher.FISHER_OPERATION(input_data, network, vector, epsilon)
print("The fisher matrix quadratic form:", FISHER.fisher_quadratic_form())
print("The fisher matrix trace:", FISHER.fisher_trace())
print("The fisher information sensitivity:", FISHER.fisher_sensitivity())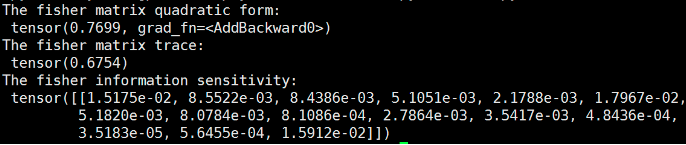
Read more

# cast draft through Avenue #
Let your words be seen by more people
How to make more high-quality content reach the reader group in a shorter path , How about reducing the cost of finding quality content for readers ? The answer is : People you don't know .
There are always people you don't know , Know what you want to know .PaperWeekly Maybe it could be a bridge , Push different backgrounds 、 Scholars and academic inspiration in different directions collide with each other , There are more possibilities .
PaperWeekly Encourage university laboratories or individuals to , Share all kinds of quality content on our platform , It can be Interpretation of the latest paper , It can also be Analysis of academic hot spots 、 Scientific research experience or Competition experience explanation etc. . We have only one purpose , Let knowledge really flow .
The basic requirements of the manuscript :
• The article is really personal Original works , Not published in public channels , For example, articles published or to be published on other platforms , Please clearly mark
• It is suggested that markdown Format writing , The pictures are sent as attachments , The picture should be clear , No copyright issues
• PaperWeekly Respect the right of authorship , And will be adopted for each original first manuscript , Provide Competitive remuneration in the industry , Specifically, according to the amount of reading and the quality of the article, the ladder system is used for settlement
Contribution channel :
• Send email :[email protected]
• Please note your immediate contact information ( WeChat ), So that we can contact the author as soon as we choose the manuscript
• You can also directly add Xiaobian wechat (pwbot02) Quick contribution , remarks : full name - contribute

△ Long press add PaperWeekly Small make up
Now? , stay 「 You know 」 We can also be found
Go to Zhihu home page and search 「PaperWeekly」
Click on 「 Focus on 」 Subscribe to our column
·

边栏推荐
- 提高MySQL深分页查询效率的三种方案
- Web知识补充
- Introduction to XML III
- Node mongodb installation
- js中的变量提升和函数提升
- The only core indicator of high-quality software architecture
- 高质量软件架构的唯一核心指标
- . Net delay queue
- CommVault cooperates with Oracle to provide metallic data management as a service on Oracle cloud
- The old-fashioned synchronized lock optimization will make it clear to you at once!
猜你喜欢
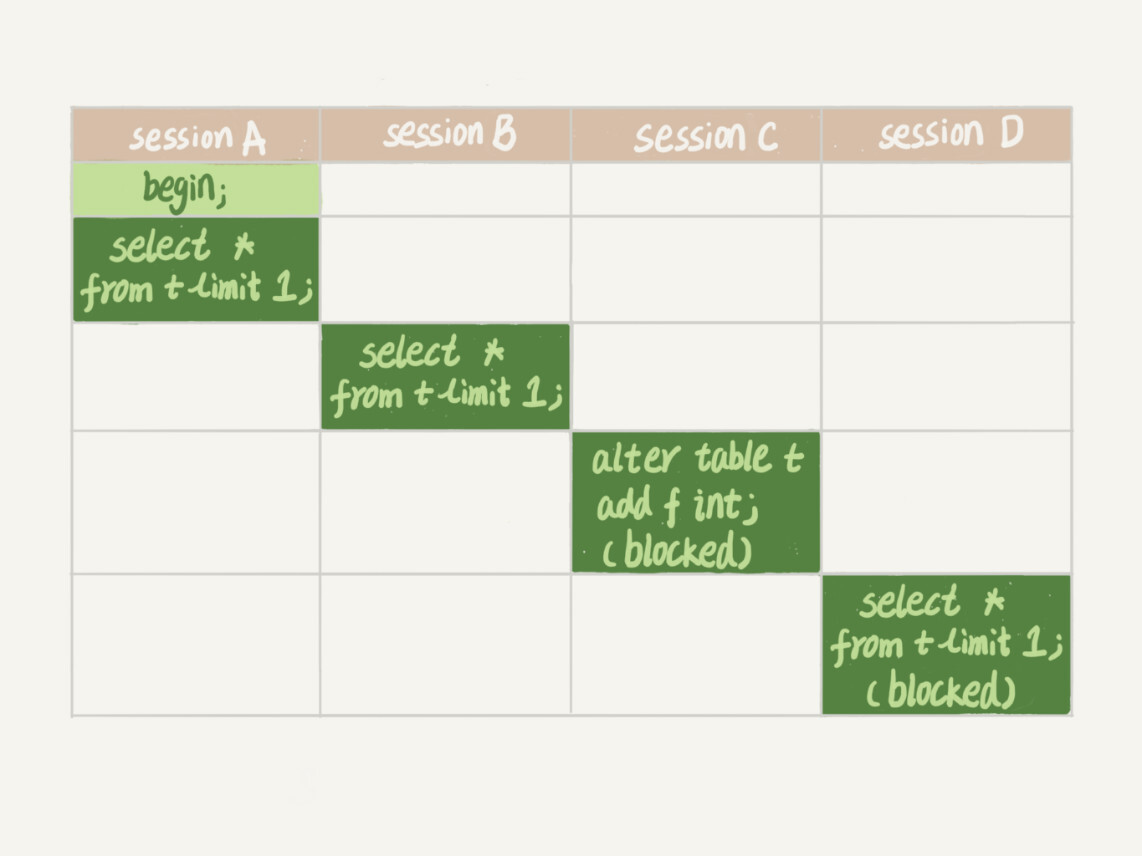
MySQL45讲——学习极客时间MySQL实战45讲笔记—— 06 | 全局锁和表锁_给表加个字段怎么有这么多阻碍
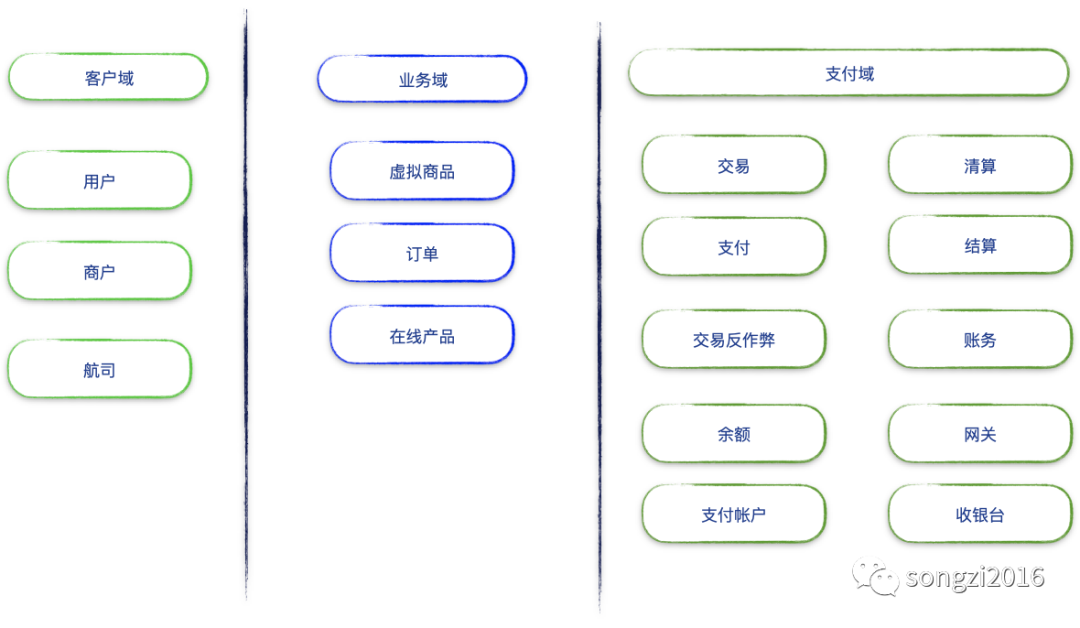
A data person understands and deepens the domain model

如何在 2022 年为 Web 应用程序选择技术堆栈
提高MySQL深分页查询效率的三种方案

面试官:Redis中哈希数据类型的内部实现方式是什么?

Oracle was named the champion of Digital Innovation Award by Ventana research

Is the outdoor LED screen waterproof?
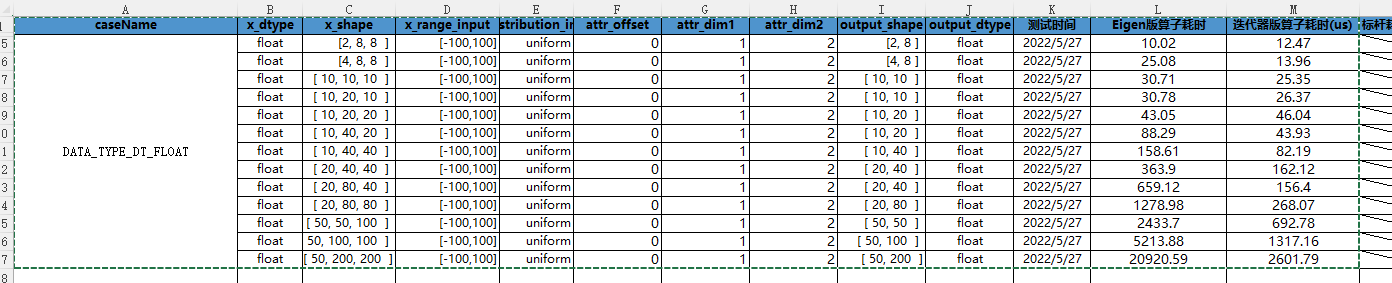
CANN算子:利用迭代器高效实现Tensor数据切割分块处理
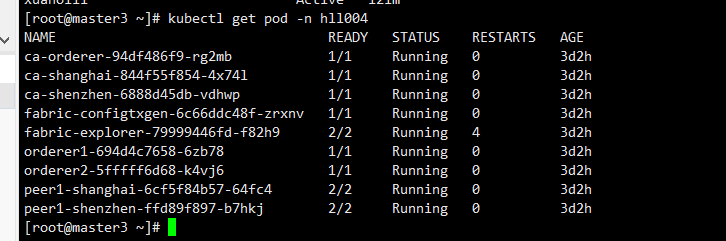
Practice: fabric user certificate revocation operation process
嵌入式编程中五个必探的“潜在错误”
随机推荐
Go zero micro service practical series (IX. ultimate optimization of seckill performance)
CommVault cooperates with Oracle to provide metallic data management as a service on Oracle cloud
Commvault 和 Oracle 合作,在 Oracle 云上提供 Metallic数据管理即服务
HAProxy高可用解决方案
美国土安全部长:国内暴力极端主义是目前美面临的最大恐怖主义威胁之一
Rsyslog configuration and use tutorial
近日小结(非技术文)
C#基础补充
一次 Keepalived 高可用的事故,让我重学了一遍它
The old-fashioned synchronized lock optimization will make it clear to you at once!
光环效应——谁说头上有光的就算英雄
WS2811 M是三通道LED驱动控制专用电路彩灯带方案开发
"Tips" to slim down Seurat objects
嵌入式编程中五个必探的“潜在错误”
C语言图书租赁管理系统
Introduction to XML I
Lick the dog until the last one has nothing (state machine)
Oracle 被 Ventana Research 评为数字创新奖总冠军
CTF competition problem solution STM32 reverse introduction
Using scrcpy projection



