Detailed explanation of Fisher information quantity detection countermeasure sample code

PaperWeekly original ·  author |  guiguzi

introduction

In the last article 《Fisher The application of information quantity in countermeasure samples 》 It elaborates on Fisher The amount of information is fighting attacks , defense , And the application in detection , And analyzed three representative papers .Fisher The amount of information is a very good mathematical tool that can be used to explore the deep causes of the antagonism behavior of the deep learning model .

This article is mainly based on Fisher A paper on information quantity to detect countermeasure samples 《Inspecting adversarial examples using the Fisher information》 Code for deep parsing , In this paper, three indexes are proposed to detect the countermeasure samples Fisher Information matrix trace ,Fisher Information quadratic form and Fisher Information sensitivity . This paper will supplement the intermediate proof process of the results directly given in the paper , And some important key details in the code will also be explained in the corresponding chapters .

Fisher Information matrix trace

Given input samples , The output of the neural network is Dimensional probability vector , On the parameters of neural network Of Fisher The continuous and discrete forms of the information matrix are as follows ：

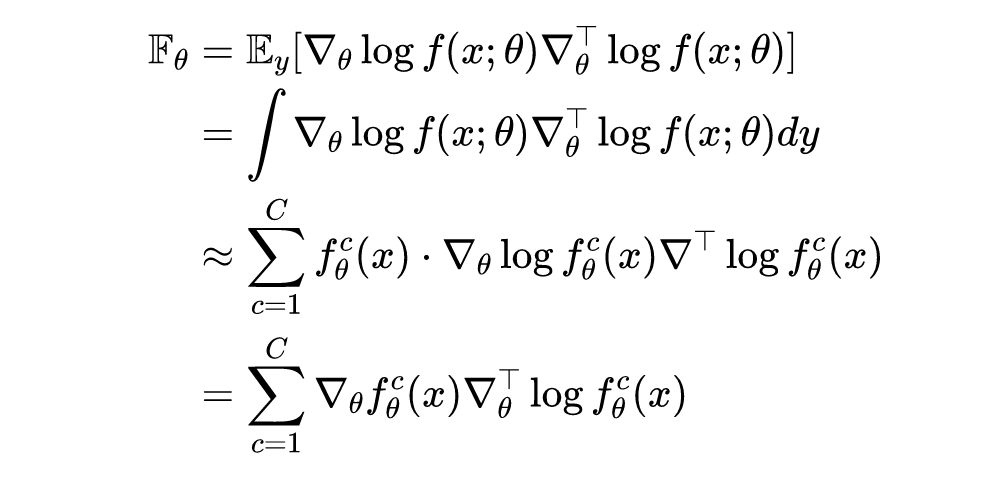
It can be seen that ,,. It should be noted that , Calculate a very small-scale neural network ,Fisher The amount of computation of the information matrix It's also tricky , What's more, those neural networks that often have hundreds of millions of parameters , The amount of calculation is much larger . Because the purpose of the original paper is to only focus on the detection of countermeasure samples , No detailed calculation is required Fisher Each exact value in the information matrix , Given the sample Fisher A value range of information quantity can be used as an indicator of detection , So... Is used in the paper Fisher The trace of the information matrix is used as the detection index , The specific calculation formula is as follows ：

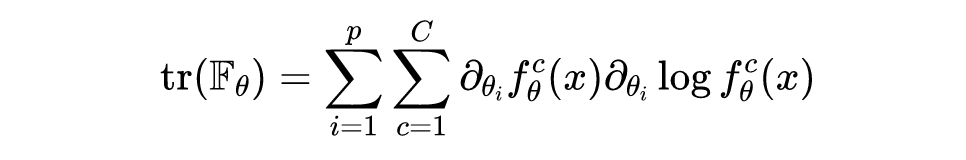
You should know that there are always some differences between theoretical analysis and practical programming , In the derivation of the above formula , It considers all the weight parameters in the neural network as a one-dimensional parameter vector , But in actual programming , The parameters of neural network are sorted by layers , But when it comes to solving Fisher The amount of information , The two cases are consistent . Suppose there is a neural network with four hidden layers , The parameters are , Then the corresponding parameters and gradients are as follows ：

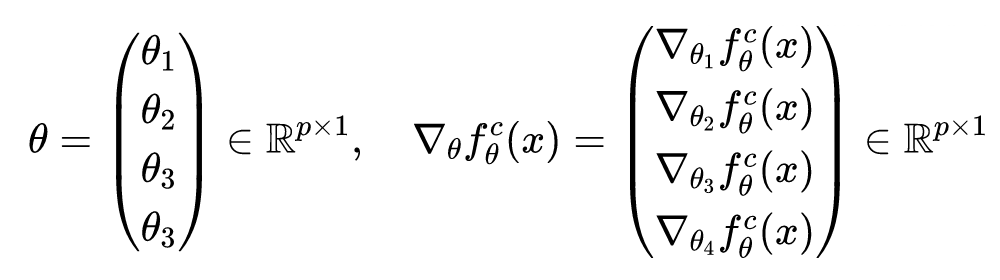
It is further known that in two cases Fisher The traces of the information matrix are equal ：

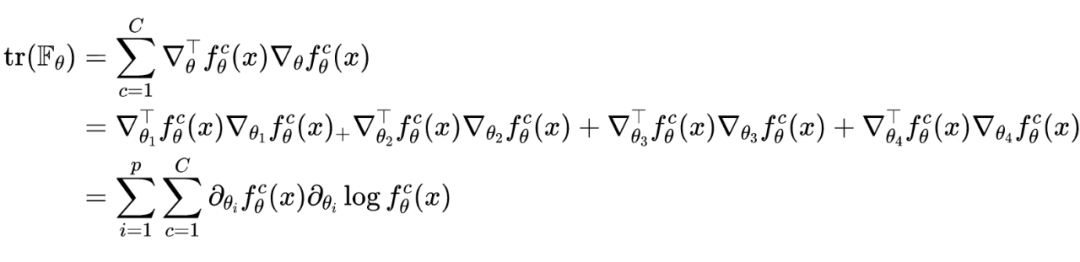
At this point, it can be found that back-propagation calculation Fisher The calculation amount of the trace of the information matrix is , Far less than the calculation Fisher The amount of computation of the information matrix .

Fisher Information quadratic form

matrix The trace of can be written as , among Is the unit vector , That is to say Elements are , The rest of the elements are , This can be understood as The average value of divergence for each parameter change . Inspired by this , Authors can choose a specific direction and measure , Instead of finding the average value on the basis of complete orthogonality , There is the following quadratic form ：

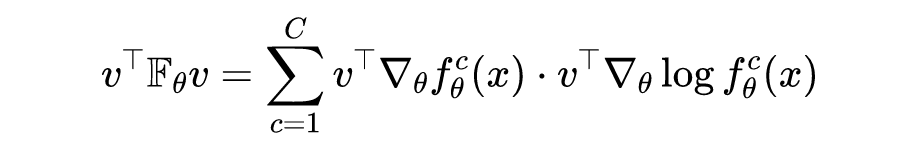
Where the given vector With the parameters And data points of ：

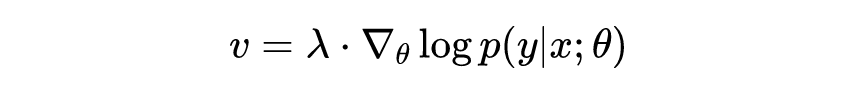
When the When normalizing , Then there is the following quadratic form ：

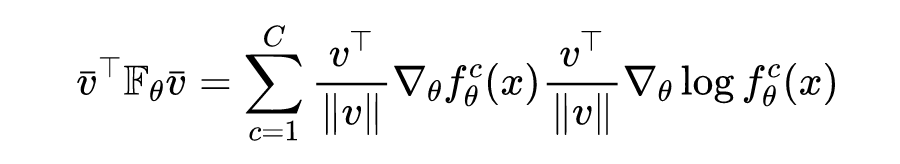
It should be noted that the selected direction is not unique , If you want to maximize the value of the quadratic form , It is Fisher The maximum eigenvalue of the matrix , The selected direction is the eigenvector corresponding to the maximum eigenvalue . It should be pointed out that ,Fisher The trace of the matrix must be greater than Fisher The maximum eigenvalue of the matrix , The specific proof is as follows ：

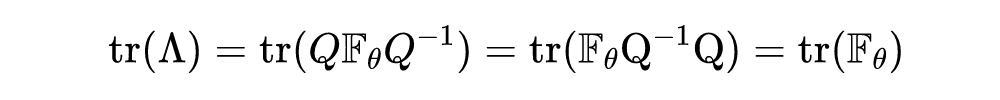
among For matrix Characteristic diagonal matrix of , Is a unit orthogonal matrix . In actual programming , To simplify the calculation , Will use the finite difference calculation to estimate the result of the back propagation gradient , According to Taylor's formula ：

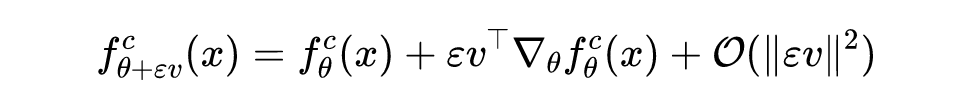
Then there are ：

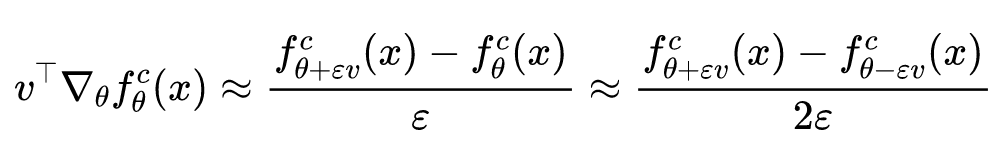
Fisher Information sensitivity

In order to further obtain available Fisher The amount of information , The author randomly introduces a single random variable into the input sample , That is to say ：

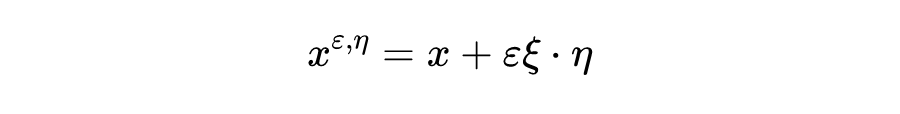
among  , also And They have the same dimensions . For this perturbed input , For its Fisher The information matrix is ：

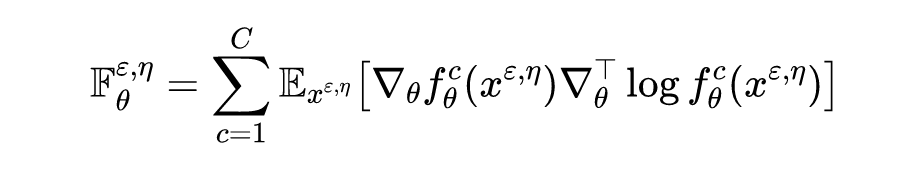
among , The... Of the matrix That's ok , The first The elements of a column can be expressed as ：

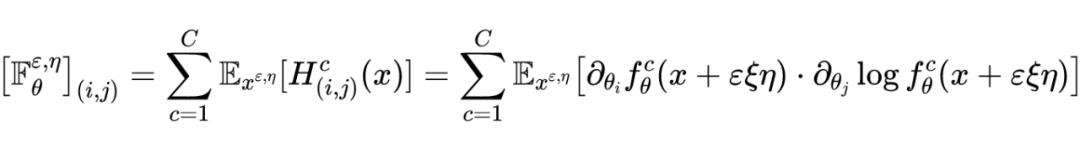
Again because Of the That's ok , The first The elements of the column are ：

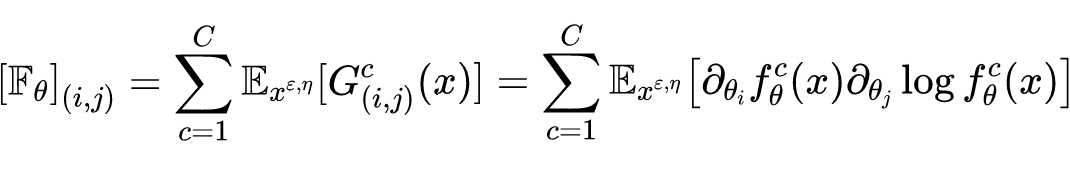
Then there is the Taylor expansion ：

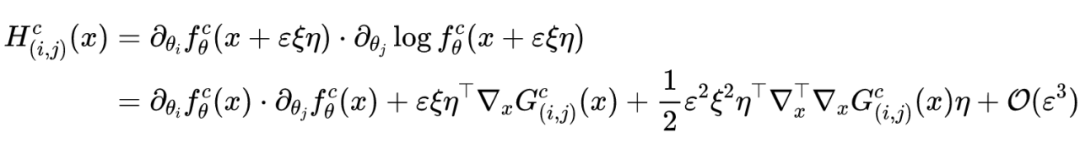
The second term of the above formula The matrix can be expressed as ：

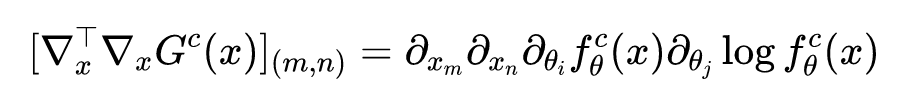
Again because Is an average of , The variance of Random variable of , Then there are ：

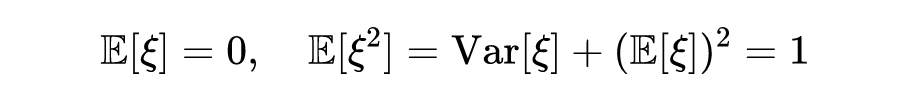
Based on the above derivation results , Then there are ：

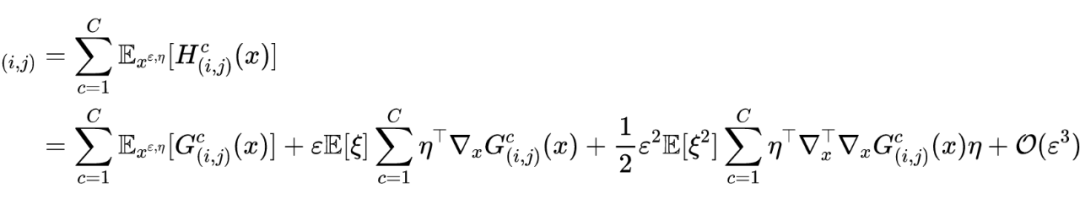
Finally, we can get the same result as in the paper ：

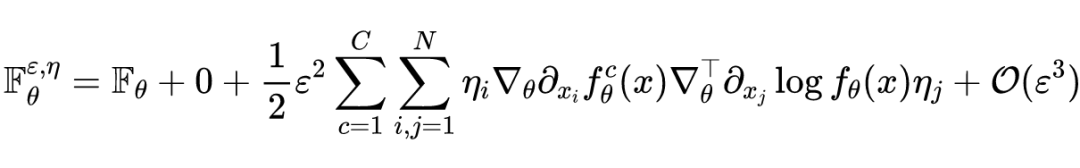
As in the previous section Fisher Matrix quadratic form , The authors also study the perturbed samples Of Fisher Finding quadratic form of matrix , Then there are ：

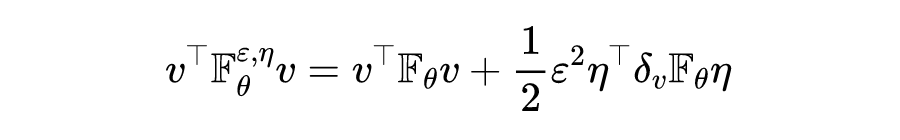
among ：

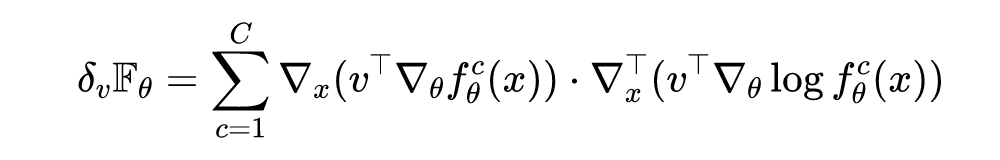
Let's say that a given perturbation vector It's the unit vector , namely . In practical programming, the finite difference method is used to estimate the result of anti back propagation gradient , Then there are ：

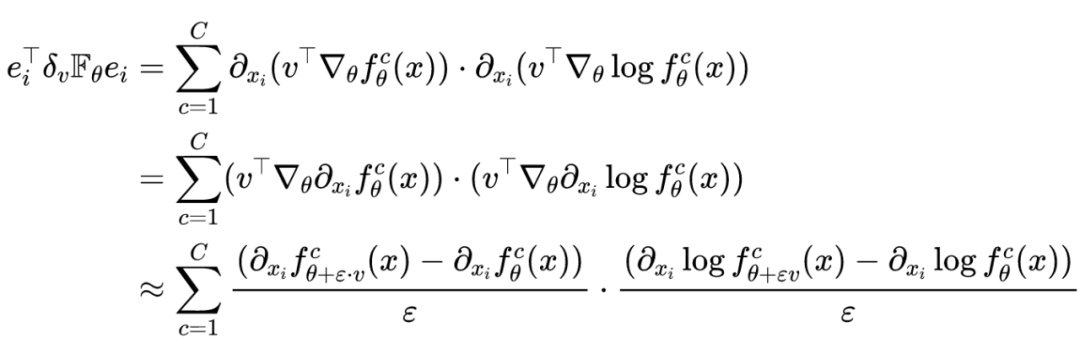
The above formula is called Fisher Information sensitivity （FIS）, It is mainly used to evaluate the Importance of input nodes .

Code example

Fisher Trace of information matrix ,Fisher Information quadratic form and Fisher The code examples and experimental results of information sensitivity are as follows , Corresponding to the principle introduction above , You can better understand the implementation details of the relevant principles in the code examples .

import torch
import torch.nn.functional as F
from copy import deepcopy


class FISHER_OPERATION(object):
        def __init__(self, input_data, network, vector, epsilon = 1e-3):
                self.input = input_data
                self.network = network
                self.vector = vector
                self.epsilon = epsilon

        # Computes the fisher matrix quadratic form along the specific vector
        def fisher_quadratic_form(self):
                fisher_sum = 0
                ## Computes the gradient of parameters of each layer
                for i, parameter in enumerate(self.network.parameters()):
                        ## Store the original parameters
                        store_data = deepcopy(parameter.data)
                        parameter.data += self.epsilon * self.vector[i]
                        log_softmax_output1 = self.network(self.input)
                        softmax_output1 = F.softmax(log_softmax_output1, dim=1)
                        parameter.data -= 2 * self.epsilon * self.vector[i]
                        log_softmax_output2 = self.network(self.input)
                        solfmax_output2 = F.softmax(log_softmax_output2, dim=1)
                        parameter.data = store_data
                        # The summation of finite difference approximate
                        fisher_sum += (((log_softmax_output1 - log_softmax_output2)/(2 * self.epsilon))*((softmax_output1 - solfmax_output2)/(2 * self.epsilon))).sum()
                return fisher_sum


        # Computes the fisher matrix trace
        def fisher_trace(self):
                fisher_trace = 0
                output = self.network(self.input)
                output_dim = output.shape[1]
                parameters = self.network.parameters()
                ## Computes the gradient of parameters of each layer
                for parameter in parameters:
                        for j in range(output_dim):
                                self.network.zero_grad()
                                log_softmax_output = self.network(self.input)
                                log_softmax_output[0,j].backward()
                                log_softmax_grad = parameter.grad
                                self.network.zero_grad()
                                softmax_output = F.softmax(self.network(self.input), dim=1)
                                softmax_output[0,j].backward()
                                softmax_grad = parameter.grad
                                fisher_trace += (log_softmax_grad * softmax_grad).sum()
                return fisher_trace


        # Computes fisher information sensitivity for x and v.
        def fisher_sensitivity(self):
                output = self.network(self.input)
                output_dim = output.shape[1]
                parameters = self.network.parameters()
                x = deepcopy(self.input.data)
                x.requires_grad = True
                fisher_sum = 0
                for i, parameter in enumerate(parameters):
                        for j in range(output_dim):
                                store_data = deepcopy(parameter.data)
                                # plus eps
                                parameter.data += self.epsilon * self.vector[i]
                                log_softmax_output1 = self.network(x)
                                log_softmax_output1[0,j].backward()
                                new_plus_log_softmax_grad = deepcopy(x.grad.data)
                                x.grad.zero_()
                                self.network.zero_grad()
                                softmax_output1 = F.softmax(self.network(x), dim=1)
                                softmax_output1[0,j].backward()
                                new_plus_softmax_grad = deepcopy(x.grad.data)
                                x.grad.zero_()
                                self.network.zero_grad()
                                # minus eps
                                parameter.data -= 2 * self.epsilon * self.vector[i]
                                log_softmax_output2 = self.network(x)
                                log_softmax_output2[0,j].backward()
                                new_minus_log_softmax_grad = deepcopy(x.grad.data)
                                x.grad.zero_()
                                self.network.zero_grad()
                                softmax_output2 = F.softmax(self.network(x), dim=1)
                                softmax_output2[0,j].backward()
                                new_minus_softmax_grad = deepcopy(x.grad.data)
                                x.grad.zero_()
                                self.network.zero_grad()
                                # reset and evaluate
                                parameter.data = store_data
                                fisher_sum += 1/(2 * self.epsilon)**2 * ((new_plus_log_softmax_grad - new_minus_log_softmax_grad)*(new_plus_softmax_grad - new_minus_softmax_grad))
                return fisher_sum

import torch
import torch.nn as nn
import fisher

network = nn.Sequential(
                nn.Linear(15,4),
                nn.Tanh(),
                nn.Linear(4,3),
                nn.LogSoftmax(dim=1)
    )
epsilon = 1e-3
input_data = torch.randn((1,15))
network.zero_grad()
output = network(input_data).max()
output.backward()
vector = []
for parameter in network.parameters():
    vector.append(parameter.grad.clone())

FISHER = fisher.FISHER_OPERATION(input_data, network, vector, epsilon)
print("The fisher matrix quadratic form:", FISHER.fisher_quadratic_form())
print("The fisher matrix trace:", FISHER.fisher_trace())
print("The fisher information sensitivity:", FISHER.fisher_sensitivity())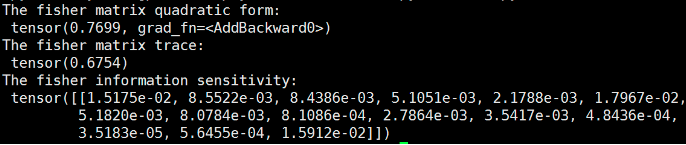

Read more

# cast draft   through Avenue #

  Let your words be seen by more people  

How to make more high-quality content reach the reader group in a shorter path , How about reducing the cost of finding quality content for readers ？ The answer is ： People you don't know .

There are always people you don't know , Know what you want to know .PaperWeekly Maybe it could be a bridge , Push different backgrounds 、 Scholars and academic inspiration in different directions collide with each other , There are more possibilities . 

PaperWeekly Encourage university laboratories or individuals to , Share all kinds of quality content on our platform , It can be Interpretation of the latest paper , It can also be Analysis of academic hot spots 、 Scientific research experience or Competition experience explanation etc. . We have only one purpose , Let knowledge really flow .

  The basic requirements of the manuscript ：

• The article is really personal Original works , Not published in public channels , For example, articles published or to be published on other platforms , Please clearly mark  

• It is suggested that  markdown  Format writing , The pictures are sent as attachments , The picture should be clear , No copyright issues

• PaperWeekly Respect the right of authorship , And will be adopted for each original first manuscript , Provide Competitive remuneration in the industry , Specifically, according to the amount of reading and the quality of the article, the ladder system is used for settlement

  Contribution channel ：

• Send email ：[email protected] 

• Please note your immediate contact information （ WeChat ）, So that we can contact the author as soon as we choose the manuscript

• You can also directly add Xiaobian wechat （pwbot02） Quick contribution , remarks ： full name - contribute

△ Long press add PaperWeekly Small make up

Now? , stay 「 You know 」 We can also be found

Go to Zhihu home page and search 「PaperWeekly」

Click on 「 Focus on 」 Subscribe to our column

·