当前位置:网站首页>CANN算子:利用迭代器高效实现Tensor数据切割分块处理
CANN算子:利用迭代器高效实现Tensor数据切割分块处理
2022-07-04 12:38:00 【华为云开发者联盟】
摘要:本文以Diagonal算子为例,介绍并详细讲解如何利用迭代器对n维Tensor进行基于位置坐标的大批量数据读取工作。
本文分享自华为云社区《CANN算子:利用迭代器高效实现Tensor数据切割分块处理》,作者: CatherineWang 。
任务场景及目标
在CANN aicpu算子开发实现中,经常需要对n维Tensor进行切片(slice)、切块(dice)、转置(transpose)、交换指定维度数据(shuffle)等操作。上述操作实质上是按照指定规律依次进行数据读取,并将读取到的数据写入新的数据地址中。
本文以Diagonal算子为例,介绍并详细讲解如何利用迭代器对n维Tensor进行基于位置坐标的大批量数据读取工作。
Diagonal算子希望对指定两个维度的数据进行对角元素的提取,最终返回张量的对角线元素。本质上该算子通过属性dim1和dim2确定一个矩阵,返回该矩阵的对角元素(存在偏移量offset),并将其放置在最后一维。非dim1和dim2的维度,将会被当成batch维度处理。
常规方案:
方案一:将shape为s,元素个数为numel的 输入Tensor:x转化为Eigen::Tensor:eigen_x;对eigen_x进行shuffle操作,将dim1和dim2换至倒数第二和倒数第一维;通过reshape操作将eigen_x变化为一个三维Eigen::Tensor:reshape_x,shape=(numel/ s[dim1]/s[dim2],s[dim1],s[dim2]);对后两维数据取对角元素,并将最终数据赋值给输出数据地址。注意:由于Eigen::Tensor<typename T, int NumIndices_>不能够动态设置维度,即NumIndices_项必须是一个具体的值,因此需要提前定义对应维度的Eigen::Tensor备用。
方案二:对于一个n维的Tensor,利用n层for循环进行数据的定位读取,并取对角值。
可以看出上述两个方案对动态大小的输入计算实现处理都较为繁琐,需要提前分情况设置对应维度的Eigen::Tensor或是for循环逻辑结构,即存在维数限制。
准备知识及分析
我们知道再AICPU中,对于一个Tensor,我们能够通过GetTensorShape、GetData等函数获得Tensor形状大小、具体数据地址等信息。但我们不能通过位置坐标的形式直接获得指定位置的数据值。
1.步长
首先介绍步长(stride)这一概念(对这部分知识已掌握的可以直接跳转下一部分内容)。stride是在指定维度dim中从一个元素跳到下一个元素所必需的步长。例如,对于一个shape=(2, 3, 4, 5)的Tensor,其stride=(60, 20, 5, 1)。因此如果想要获取到上述Tensor中位置坐标为[1, 2, 1, 3]的数据,只需要找到数据地址中第108(=60*1+20*2+5*1+3)位对应值。
2.迭代器
定义迭代器PositionIterator,包含私有成员pos_和shape_,其中pos_为初始位置,shape_为标准形状。通过重载++符号,对pos_进行修改,实现迭代器的自增操作。基于上述迭代器,可以实现对给定的shape依次取位操作。如给定对于给定的shape=(d_1,d_2,…,d_n),从初始位置(0,0,…,0)开始,依次取(0,0,…,0,0), (0,0,…,0,1),…,(0,0,…,0,d_n-1), (0,0,…,1,0), (0,0,…,1,1),…, (d_1 - 1,d_2 - 1,…,d_{n-1}-1,d_{n}-1).
事实上,可以将上述迭代器理解为一种进制,对于给定的标准形状shape_=(d_1,d_2,…,d_n),第i位运算时便是逢d_i进1。同时通过PositionIterator .End()控制迭代器的结束。具体实现如下:
template <typename T>class PositionIterator { public: PositionIterator(){}; ~PositionIterator(){}; PositionIterator(std::vector<T> stt, std::vector<T> sh) { if (stt.size() != sh.size()) { PositionIterator(); } else { for (unsigned int i = 0; i < sh.size(); i++) { if (stt[i] >= sh[i]) { PositionIterator(); } } pos_ = stt; shape_ = sh; } } PositionIterator operator++() { pos_[shape_.size() - 1] += 1; for (unsigned int i = shape_.size() - 1; i > 0; i--) { if (pos_[i] / shape_[i] != 0) { pos_[i - 1] += pos_[i] / shape_[i]; pos_[i] = pos_[i] % shape_[i]; } } return *this; } bool End() { if (pos_[0] != shape_[0]) { return false; } return true; } std::vector<T> GetPos() { return pos_; } std::vector<T> GetShape() { return shape_; } private: std::vector<T> pos_; std::vector<T> shape_;};Diagonal算子的实现
利用迭代器,在一般情况下,我们只需要两层for循环,便可以实现Diagonal算子的计算过程。第一层for循环用于确定除dim1和dim2维度的位置坐标,第二层for循环用于对dim1和dim2对应维度确定对角元素位置,通过这样的两层for循环,便可将对角元素位置确定。通过这样的取值处理,相较于Eigen实现思路,计算速度有着明显的提升,且无维度限制,st测试结果对比如下:
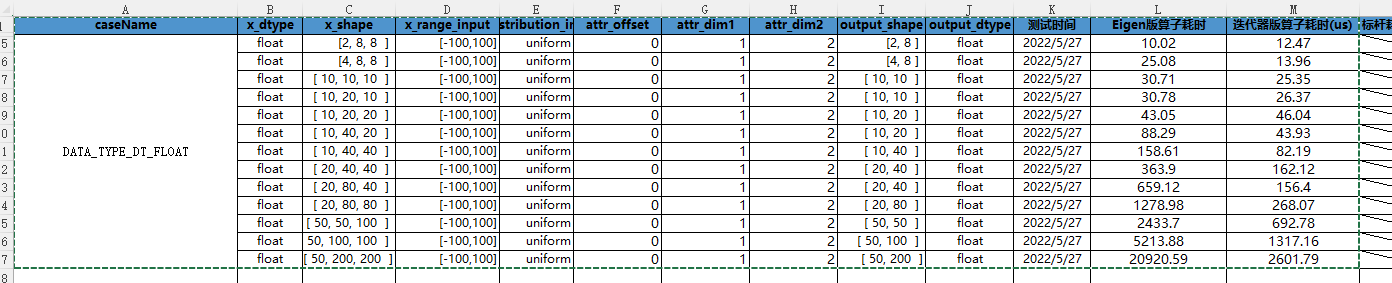
具体实现可参见如下代码:
template <typename T>uint32_t DiagonalCpuKernel::DoComputeType(CpuKernelContext &ctx, const int64_t &offset, const int64_t &dim1, const int64_t &dim2) { // Get the inuput and output Tensor *input_x = ctx.Input(0); Tensor *y = ctx.Output(0); // Get some information of input auto x_shape = input_x->GetTensorShape(); std::vector<int64_t> x_shape_ = x_shape->GetDimSizes(); const int64_t x_dim = x_shape->GetDims(); auto dataptr = reinterpret_cast<T *>(ctx.Input(0)->GetData()); auto y_dataptr = reinterpret_cast<T *>(y->GetData()); // Compute // 首先计算出对角线元素个数 int64_t dsize = OffsetSize(offset, dim1, dim2, x_shape_); // 生成输入Tensor的步长向量x_stride std::vector<int64_t> x_stride = ConstructStride<int64_t>(x_shape_); // 分情况讨论,2维和大于2维的情况 if (x_dim != N2) { //set the vx_shape and vx_stride // 生成x_shape和x_stride中除去dim1和dim2对应值的vx_shape与vx_stride std::vector<int64_t> vx_shape, vx_stride; for (unsigned int tmp_dim = 0; tmp_dim < x_shape_.size(); tmp_dim++) { if (tmp_dim != dim1 && tmp_dim != dim2) { vx_shape.push_back(x_shape_[tmp_dim]); vx_stride.push_back(x_stride[tmp_dim]); } } // set the y_shape, y_stride, vy_stride // 生成输出Tensor的形状及步长向量:y_shape和y_stride std::vector<int64_t> y_shape = vx_shape; y_shape.push_back(dsize); std::vector<int64_t> y_stride = ConstructStride<int64_t>(y_shape); // 生成输出Tensor的出去最后一维的步长向量:vy_stride std::vector<int64_t> vy_stride = y_stride; vy_stride.pop_back(); // 读取对角数据 std::vector<int64_t> v_start(vx_shape.size(), 0); for (PositionIterator<int64_t> myiter(v_start, vx_shape); !myiter.End(); ++myiter) { // 利用迭代器确定除dim1和dim2维度的位置坐标 auto p = myiter.GetPos(); // 通过步长向量和位置坐标计算出输入和输出的基础位置值base_pos1和outbase_pos int64_t base_pos1 = MulSum<int64_t>(p, vx_stride); int64_t outbase_pos = MulSum<int64_t>(p, vy_stride); for (int i = 0; i < dsize; i++) { // 结合前面计算出的基础位置值,对dim1和dim2对应维度确定对角元素位置,并赋值给输出数据地址(get_data涉及对上对角还是下对角取元素,不影响对迭代器作用的理解) int64_t base_pos2 = i * (x_stride[dim1] + x_stride[dim2]); int64_t arr[N2] = {x_stride[dim1], x_stride[dim2]}; y_dataptr[outbase_pos + i] = get_data(base_pos1 + base_pos2, offset, arr, dataptr); } } } else { for (int i = 0; i < dsize; i++) { int64_t base_pos = i * (x_stride[dim1] + x_stride[dim2]); int64_t arr[N2] = {x_stride[dim1], x_stride[dim2]}; y_dataptr[i] = get_data(base_pos, offset, arr, dataptr); } } return KERNEL_STATUS_OK;}迭代器的其他用法
1、数据切条:如Sort算子中,用迭代器对Tensor数据关于tmp_axis维度进行取条,以进行后续的排序操作。
for (position_iterator<int64_t> mit(v_start, v_shape); !mit.end(); ++mit) { auto p = mit.get_pos(); int axis_len = input_shape_[tmp_axis]; std::vector<ValueIndex<T>> data_(axis_len); int base_pos = mul_sum<int64_t>(p, v_stride); for (int32_t i = 0; i < axis_len; i++) { data_[i].value = x_dataptr[base_pos + i * input_stride[tmp_axis]]; data_[i].index = i; }2、数据切块:切块处理可以利用两个迭代器循环叠加,也可以利用一个迭代器和两个坐标位置for循环
3、关于指定维度dim,对Tensor降维拆分为N子Tensor:如UniqueConsecutive算子中,首先需要关于属性axis维,将原本的Tensor数据拆分为input_shape[axis]个子Tensor(此处用vector存储Tensor中的数据)。
std::vector<std::vector<T1>> data_; for (int64_t i = 0; i < dim0; i++) { std::vector<T1> tmp_v1; for (PositionIterator<int64_t> mit(v_start, v_shape); !mit.End(); ++mit) { auto pos = mit.GetPos(); tmp_v1.push_back( x_dataptr[MulSum<int64_t>(pos, v_stride) + i * input_stride[axis]]); } data_.push_back(tmp_v1); }
边栏推荐
- Talk about the design and implementation logic of payment process
- C#/VB.NET 给PDF文档添加文本/图像水印
- When to use pointers in go?
- Master the use of auto analyze in data warehouse
- Jetson TX2 configures common libraries such as tensorflow and pytoch
- [Yu Yue education] 233 pre school children's language education reference questions in the spring of 2019 of the National Open University
- 室外LED屏幕防水吗?
- 认知的定义
- CANN算子:利用迭代器高效实现Tensor数据切割分块处理
- 洞见科技解决方案总监薛婧:联邦学习助力数据要素安全流通
猜你喜欢
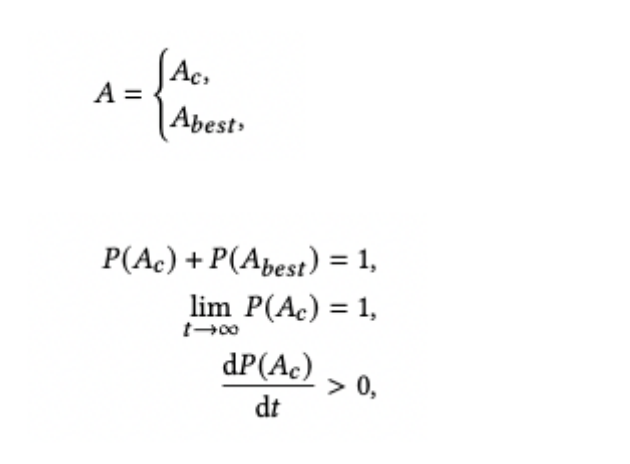
面向个性化需求的在线云数据库混合调优系统 | SIGMOD 2022入选论文解读

n++也不靠谱
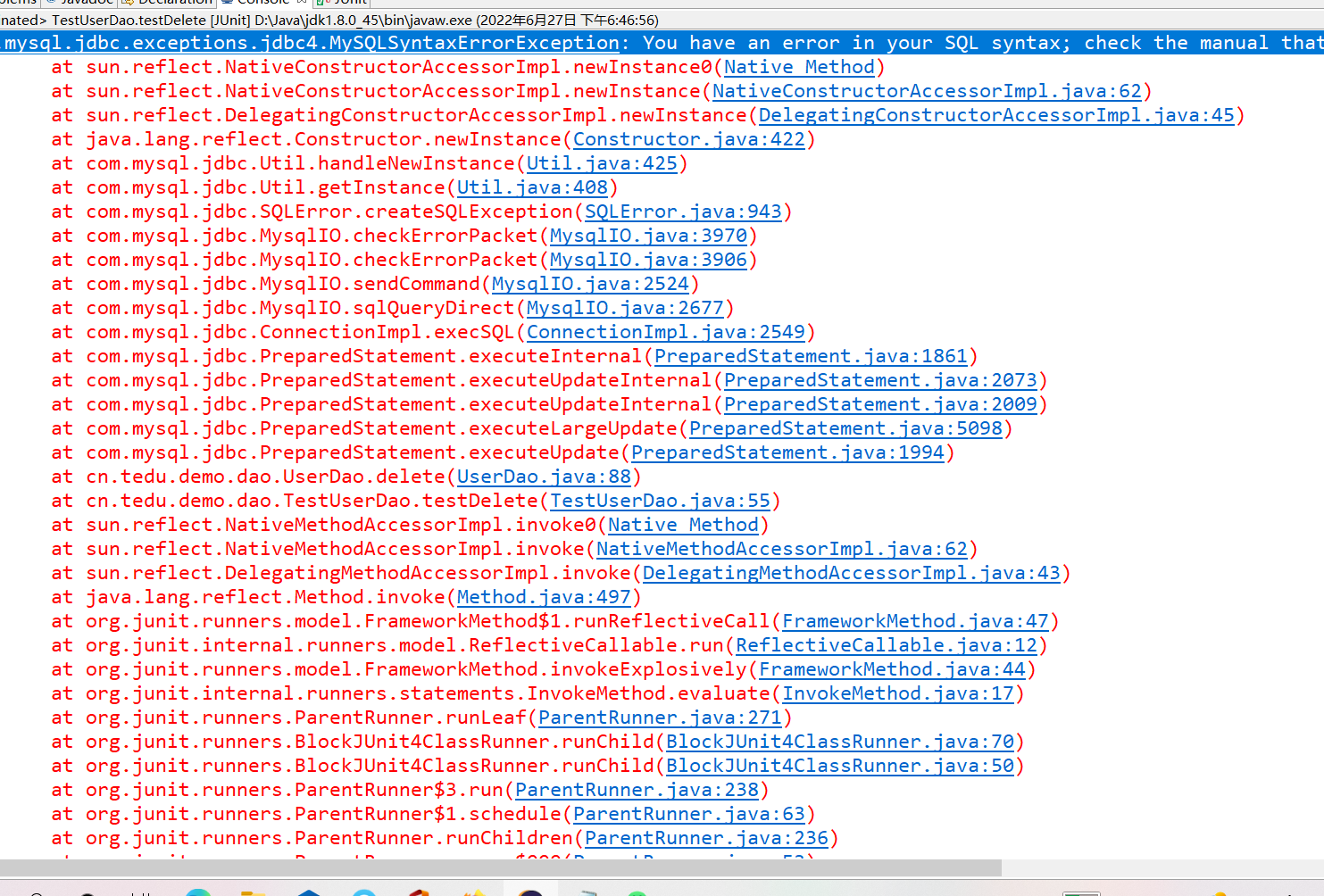
eclipse链接数据库中测试SQL语句删除出现SQL语句语法错误

MDK在头文件中使用预编译器时,#ifdef 无效的问题
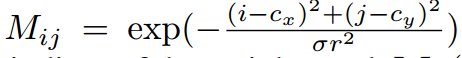
CVPR 2022 | TransFusion:用Transformer进行3D目标检测的激光雷达-相机融合

Zhongang Mining: in order to ensure sufficient supply of fluorite, it is imperative to open source and save flow
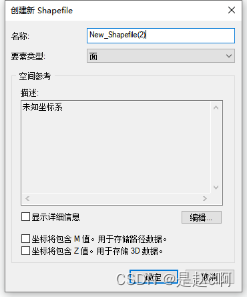
ArcGIS uses grid processing tools for image clipping
After installing vscode, the program runs (an include error is detected, please update the includepath, which has been solved for this translation unit (waveform curve is disabled) and (the source fil
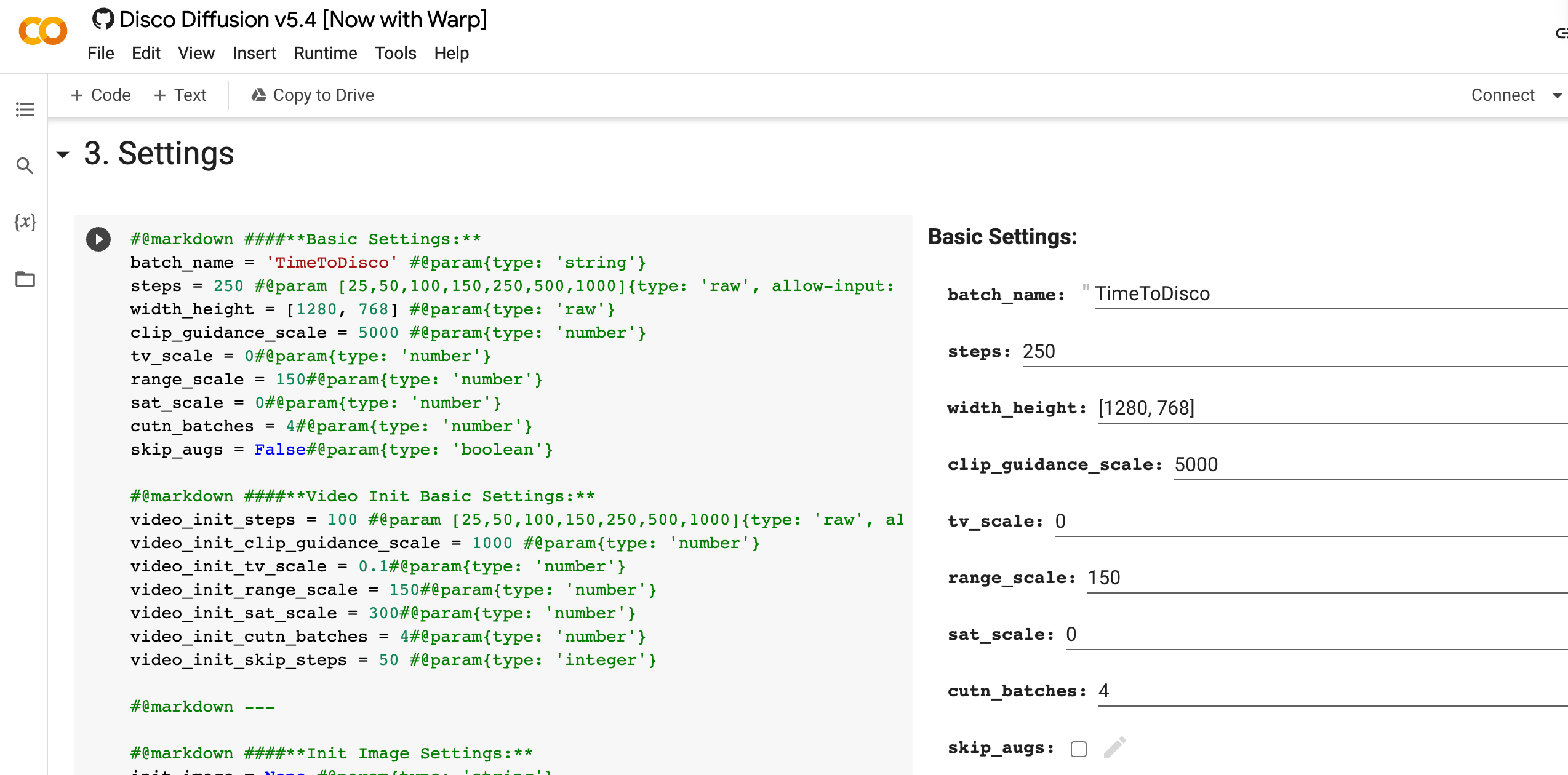
AI 绘画极简教程

ISO 27001 Information Security Management System Certification
随机推荐
使用 NSProxy 实现消息转发
jsonp
[data clustering] section 3 of Chapter 4: DBSCAN performance analysis, advantages and disadvantages, and parameter selection methods
实战:fabric 用户证书吊销操作流程
分布式事务相关概念与理论
Interviewer: what is the difference between redis expiration deletion strategy and memory obsolescence strategy?
Can Console. Clear be used to only clear a line instead of whole console?
R language -- readr package reads and writes data
面试官:Redis 过期删除策略和内存淘汰策略有什么区别?
16.内存使用与分段
实时云交互如何助力教育行业发展
ArcGis利用栅格处理工具进行影像裁剪
诸神黄昏时代的对比学习
【AI系统前沿动态第40期】Hinton:我的深度学习生涯与研究心法;Google辟谣放弃TensorFlow;封神框架正式开源
Full arrangement (medium difficulty)
AI 绘画极简教程
游戏启动后提示安装HMS Core,点击取消,未再次提示安装HMS Core(初始化失败返回907135003)
Reinforcement learning - learning notes 1 | basic concepts
MySQL three-level distribution agent relationship storage
Jetson TX2配置Tensorflow、Pytorch等常用库